Đề Xuất Thuật Toán Khai Thác Dàn Các Tập Phổ Biến Đóng Và Cải Tiến

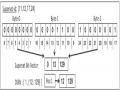
Cho DSBV X = {8,{2,0,0,1,5,7}} và DSBV Y = {10,{2,3,1,0,0,5}}.hình bên dưới

minh họa việc giao 2 DSBV.

xMin: 3 xMax: 8

2	0	0	1	5	7
		2	3	1	0	0	5

Có thể bạn quan tâm!

• Khai thác dàn tập phổ biến đóng sử dụng cấu trúc DSBV - 2
• Phương Pháp Nghiên Cứu Và Đối Tượng Nghiên Cứu
• Cơ Sở Dữ Liệu Giao Dịch Theo Chiều Dọc Dùng Bit Vector.
• Đặc Tả Và Phân Tích Thuật Toán Input: Csdl Giao Dịch: Db, Minsup.
• Khai thác dàn tập phổ biến đóng sử dụng cấu trúc DSBV - 7
• Khai thác dàn tập phổ biến đóng sử dụng cấu trúc DSBV - 8

Xem toàn bộ 72 trang tài liệu này.

X:

Y:

Bitwise AND

pY= yMin: 5 yMax: 10

rMin: 5

Result: {7, {1, 1}}

0

1

1

0

Xóa 0

1

1

P= 7

rMax:8

Hình 2.2: Giao 2 DSBVs

5.2.4 Cập nhật 1 DSBV

Để truyền thông tin FCS mới vào cấu trúc DSBV lên phía trên trong quá trình đệ qui, phải cập nhật DSBV của một tập hạng mục. Việc cập nhật này được thực hiện bằng phép toán hội DSBV của hai FCIs. Phép hội tập hợp này được thực hiện bằng phép toán OR trên bit liên tục giữa các byte của hai DSBV.

Đặc tả thuật toán bằng mã giả như sau:

DBV SetHelper::Union2DBV(DBV* X,DBV* Y)

{

xMax=X->iNonZeroByte;//chỉ số byte cao của X

xMin=X->iNonZeroByte - X->bitVec.size()-1;//chỉ số byte thấp của X yMax=Y->iNonZeroByte;//chỉ số byte cao của Y

yMin=Y->iNonZeroByte - Y->bitVec.size()-1;//chỉ số byte thấp của Y rMax=min(xMax,yMax);//chỉ số byte cao của kết quả rMin=max(xMin,yMin);//chỉ số byte thấp của kết quả

-for(i=rMin to rMax) Result = X bitwise OR Y;

return result;

}

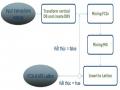
Cho DSBV X = {8,{2,0,0,1,5,7}} và DSBV Y = {10,{2,3,1,0,0,5}}. Hình bên dưới

minh họa việc hội 2 DSBV.

xMin: 3 xMax: 8

2	0	0	1	5	7
		2	3	1	0	0	5

X:

Y:

Bitwise OR

pY= yMin: 5 yMax: 10

2

0

2

3

5

7

0

5

rMin: 3

Result:{10,{2,0,2,3,5,7,0,5}} rMax: 10

P= 10

Hình 2.3: Hội 2 DSBVs

Chương 3: ĐỀ XUẤT THUẬT TOÁN KHAI THÁC DÀN CÁC TẬP PHỔ BIẾN ĐÓNG VÀ CẢI TIẾN

Trong phần này, giới thiệu phương pháp tiếp cận mới của luận văn áp dụng kỹ thuật Bit-Vector [24] trong việc khai thác các FCI với cấu trúc Dàn để tìm các luật kết hợp không dư thừa (NARs). Thông qua việc sử dụng có hiệu quả cấu trúc DSBV để lưu trữ thông tin FCS của một tập phổ biến đóng, xây dựng mối quan hệ giữa các tập hạng mục một cách hiệu quả trong Dàn.

Thuật toán BVCL: Bit Vector oriented frequent Closed itemset Lattice mining.

1. Phát biểu bài toán khai thác Dàn các tập phổ biến đóng

Khai thác Dàn các tập phổ biến đóng là đi tìm tất cả các tập phổ biến đóng thõa ngưỡng minsup do người dùng đặt ra từ CSDL giao dịch, thiết lập mối quan hệ cha con của chúng tạo thành cây phân cấp mà các nút là các tập phổ biến đóng vừa nêu.

Quá trình này gồm 2 giai đoạn chính:

Giai đoạn 1: Cho cơ sở dữ liệu giao dịch D với ngưỡng minSup làm đầu vào, cơ sở dữ liệu ngang (tid × itemset) được chuyển đổi thành dạng dọc (item x tidset) sau khi loại bỏ các item không phổ biến (có hỗ trợ < minSup) để chuẩn bị trước cho thuật toán. Xem Bảng 2.3.

Giai đoạn 2: Cho C đại diện cho tập các tập phổ biến đóng {C1, C2,. . . , Cm} và L đại diện cho Dàn các tập phổ biến đóng, bao gồm một tập các nút {N1, N2,. . . , Nm}. Thuật toán của chúng ta liệt kê tất cả các tập phổ biến đóng, mô tả sự phụ thuộc của chúng trong Dàn.

Định nghĩa 1: Dàn FCIs và tập luật không dư thừa NARs

Cho CSDL D = {t1, t2,. . . , tn} của n giao dịch và {x1, x2,. . . , xm} của m item có ngưỡng hỗ trợ tối thiểu (minSup) và độ tin cậy tối thiểu (minConf). Vấn đề cần là khai thác Dàn các tập phổ biến đóng (FCIL) L = (N,R) và tập các luật không dư thừa là A.

Trong đó N = {N1, N2... Ni}, một tập các nút với Ni ∈ N chứa các tập phổ biến đóng Ci ∈ C (tất cả các tập phổ biến đóng thõa minSup) và:

R = { 𝑅𝑖𝑗 ∶ 𝑁𝑖 → 𝑁𝑗 |𝑁𝑖 , 𝑁𝑗 ∈ N and 𝑁𝑗 = minimal frequent closed superset( 𝑁𝑖 ), 1 ≤ 𝑖, 𝑗 ≤ 𝑙 }

A = { 𝐴𝑘 ∶ 𝐶𝑝 ⇒ ( 𝐶𝑞 − 𝐶𝑝 ) | 𝐶𝑝 , 𝐶𝑞 ∈ C and 𝐶𝑝 ⊂ 𝐶𝑞 & 𝐶𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒( 𝐴𝑘 ) ≥ 𝑚𝑖𝑛𝐶𝑜𝑛𝑓 , 1 ≤ 𝑝, 𝑞 ≤ 𝑙 }.

BVCL khai thác tất cả các tập phổ biến đóng C thõa ngưỡng minSup từ một cơ sở dữ liệu D và trong quá trình khai thác tập phổ biến đóng Ci ∈ C, tập các bao đóng tối tiểu được xác định. BVCL kết nối mọi FCI với tập các bao đóng tối tiểu của nó để thiết lập mối quan hệ cha – con giữa các nodes của Dàn, theo hướng bottom-up.

2. Thuật Toán BVCL

Cách tiếp cận của thuật toán là phát hiện ra tất cả các tập phổ biến đóng theo hướng depth first, bằng cách khai thác thông tin tidset và superset. Đặc tả thông tin tidset của một tập hạng mục bằng cách sử dụng cấu trúc dynamic bit-vector (DBV). Để lưu trữ thông tin bao đóng (closed superset) của 1 tập, luận văn đề xuất một cấu trúc dữ liệu mới gọi là DSBV. Các cấu trúc dữ liệu này được sử dụng để thiết lập mối quan hệ cha - con trên theo hướng bottom - up trong các tập phổ biến đóng của Dàn, cho phép BVCL vượt trội hơn các phương pháp khai thác các tập phổ biến đóng và khai thác Dàn khác.

BVCL bắt đầu quá trình khai thác bằng cách xác định tập các hạng mục phổ biến {x1, x2,. . . , xm}. Các hạng mục này được kết hợp với nhau dựa trên các thuộc tính subsuming như mô tả trong Chương 2. Trong quá trình kết hợp này, chi phí cho tập con được hạn chế bằng cách duy trì 2 danh sách riêng biệt (subsuming and non-subsuming list). Các danh sách này được định nghĩa như sau:

Định nghĩa 2: Subsuming list (SL) and non-subsuming list (nSL):

Cho tập hạng mục X = {x1, x2, . . . ,xl}, và một item y.

Nếu X được subsumed bởi y thì y được gọi là subsuming item cho X. Ngược lại thì y gọi là non - subsuming với X.

Subsuming, non-subsuming items tương ứng được xây dựng với các danh sách là SLX và nSLX.

Xem xét Bảng 2.3. Item “A” được subsumed bởi item “P” theo bổ đề 1.

DBV“A" ⊆DBV“P" vì DBV“A" = DBV“A" ∩ DBV“P" DBV“A" = {0, {29}} and DBV“P" = {0, {31}}.

Tương tự, “A” được subsumed bởi item “N” và “L”. Vì vậy, subsuming List của A là SL“A" = {“P ”, “N ”, “L ”}. Non-subsuming List của A là nSL “A " = {“C ”, “M ”, “D ”}.

Cách tiếp cận của luận văn là sắp xếp theo thứ tự tăng dần hạng mục phổ biến dựa trên độ hỗ trợ của chúng. Với mỗi hạng mục phổ biến xi ∈ L = { x1 , x2 , . . . , xm }, 2 danh sách SLxi = { x’1 , x’2 , . . . , x’p } và nSLxi = { x”1 , x”2 , . . . , x”q } được thiết lập. Sau đó xi được sáp nhập với các hạng mục của Slxi theo bổ đề 2, kết quả là tập đóng Ck (FCI thứ k của xi). Non-subsuming list nSLCk của Ck được khởi tạo với non-subsuming list của xi, nSLxi.

Bây giờ tập phổ biến đóng Ck bắt đầu gọi đệ quy khai thác tập phổ biến đóng mới là Ck+1 bằng cách kết hợp Ck với x”j bất kì ∈ nSLCk. Quá trình kết hợp theo sau quá trình kiểm tra subsume được lặp lại cho các hạng mục còn lại { x"j+1 , . . . , x"q } của nSLCk và tiếp tục xây dựng các danh sách subsuming và non-subsuming theo cách tương tự. Tập Ck+1 được khai thác gần nhất với danh sách non-subsuming của nó tiếp tục quá trình khai thác các FCI theo cách depth first. Do đó, thuật toán xây dựng quá trình kết hợp, tránh việc kiểm tra tập con bị lặp lại như thuật toán DBV-Miner như sau:

Bổ đề 3:

SLCk và nSLCk đại diện cho danh sách subsuming và non-subsuming tương ứng của tập phổ biến đóng thứ k là Ck. Quá trình kết hợp yêu cầu không kiểm tra tập con (Subset) trong suốt quá trình phát sinh tập FCI thứ k+1 là Ck+1 từ Ck và xj ∈ nSLCk bất kì.

Chứng minh:

Tập phổ biến đóng Ck+1 thu được từ việc kết hợp Ck với hạng mục x j ∈ nSLCk bất kì, hay Ck+1= Ck U xj. Ck+1 được tính bằng cách lặp lại quá trình kiểm tra subsume với các hạng mục còn lại {xj+1, xj+2,. . . , xm } ∈ nSLCk dùng bổ đề 1 và bổ đề 2. Vì chỉ có các mục xj ∈ nSLCk đóng góp xây dựng Ck +1 bằng cách mở rộng Ck và 𝑥𝑗 ⊈ 𝐶𝑘 , nên không cần thực hiện kiểm tra tập con để tránh tạo ra các tập thừa.

DBVCk+1 và DSBVCk+1 được xác định từ DBV và DSBV của Ck và xj. Tuy nhiên, cần xác định xem Ck+1 có tạo ra tập không đóng nào không sau khi kiểm tra sup(Ck+1) ≥ minSup. Tập S = {s1, s2,. . . , sl} là bao đóng của Ck+1 được xác định từ DSBVCk+1 áp dụng các thuật toán thảo luận trong Phần 5.2.1. Nếu độ hỗ trợ của bất kì bao đóng si ∈ S = sup (Ck+1) thì Ck+1 sẽ bị loại bỏ như là tập không đóng. Nếu không, quá trình subsuming được bắt đầu để tính toán bao đóng của Ck +1. Trong khi đó, DSBVCk +1 được cập nhật bởi DSBV của các hạng mục từ SLCk +1. Việc đệ qui của các tập đóng trong các nhánh sẽ chấm dứt ngay sau khi danh sách non-subsuming của các hạng mục là rỗng.

Trong phương pháp này, mỗi tập đóng Ck +1 truyền thông tin FCS của nó thông qua DSBVCk +1 ngược lên tập đóng Ck, từ Ck mà nó đã được sinh ra và các tập hạng mục của SLCk+1. Kỹ thuật này đảm bảo rằng DSBV của một FCI sẽ chứa thông tin FCS hoàn chỉnh của nó sau khi phát sinh tất cả các tập con cháu FCI của nó. Vì vậy, chúng ta có phần bổ đề sau đây.

Bổ đề 4:

Chiến lược dẫn xuất depth first và kỹ thuật kết hợp nhân bản cập nhật Ck+1 (từ Ck và non - subsuming list) đảm bảo tính hoàn chỉnh của thông tin FCS vào trong cấu trúc DSBV của một tập FCI.

Chứng minh:

Một tập phổ biến đóng C thừa hưởng thông tin (FCS) vào cấu trúc DSBV của nó từ các FCIs Cha (phía trên trong cây đệ qui). Sau đó, C đệ qui phát sinh tất cả con cháu FCIs trong 1 nhánh bằng cách mở rộng nó với các hạng mục của danh sách non-

subsuming (nSLC). Quá trình depth first khai thác các FCIs mới kết thúc ngay khi nSLC rỗng, có nghĩa là FCIs có thể được khai thác thêm từ C. Hơn nữa, DSBV của C (DSBVC) được cập nhật bởi các DSBVs của các FCIs con cháu của nó là một quá trình truyền thông tin FCS dọc theo nhánh. Do đó, DSBVC hoàn tất thu thập thông tin FCS ngay khi depth first thu được của tất cả các FCIs con cháu của C chấm dứt.

Vì cấu trúc DSBV của mỗi FCI chứa thông tin FCS hoàn chỉnh được nêu trong bổ đề 4, nó có thể được sử dụng hiệu quả trong việc phát hiện các phát sinh tập không đóng. Sau khi depth first phát sinh tất cả con cháu FCIs, một tập đóng đã khởi tạo nhánh, tiếp tục khai thác các tập phát sinh mới bằng cách kết hợp chính nó với các hạng mục non - subsuming còn lại. Bổ đề sau đảm bảo quá trình loại bỏ việc phát sinh các tập thừa thông qua thuộc tính DSBV của một Itemset.

Bổ đề 5:

Việc phát sinh các tập không đóng có thể được loại bỏ trước khi tính toán bao đóng các tập trong BVCL.

Chứng minh:

Cho X là tập phát sinh của tập ứng viên đóng C= X U xj (xj subsumes X). X = C’ U xi, DSBVX = DSBVC’ ∩ DSBVxi (giả sử tập đóng C’ đã khai thác) và DSBVC = DSBVX ∩ DSBVxj . Với : xi , xj nSLC’ (non-subsuminglist of C’ ), j > i. Các tập SX = { s’1 , s’2 , . . .

, s’n } và SC = { s”1 , s”2 , . . . , s”m } đại diện thông tin của X và C được xác định từ DSBVX và DSBVC, trong đó SC ⊆ SX vì DSBVC ⊆ DSBVX.. Nếu vẫn còn 1 bao đóng s”∈ S C mà sup (s”) = sup (C), thì C sẽ bị loại bỏ như một tập không đóng. Tuy nhiên, Nếu C là tập không đóng thì nó có thể được loại bỏ sớm bằng cách loại bỏ phát sinh X của nó trước khi tính toán bao đóng thông qua quá trình lặp subsuming vì s”SC ⊆ SX tức là s”SX và sup (X) = sup (C) = sup (s”).

BVCL tính toán cấu trúc Dàn bằng cách mở rộng cây khai thác FCI. Nó xem xét tất cả các tập phổ biến đóng Ci ∈ C của cây theo trật tự ngang trong suốt quá trình xây dựng từ dưới lên của cấu trúc Dàn L. Do đó, DSBV của Ci được tiếp tục sử dụng để khai thác bao

đóng tối tiểu của nó kí hiệu bởi tập S’ = {s’1 , s’2 , . . . , s’l} Ci được liên kết với các nút bao gồm tất cả các tập đóng của S' (đã được chèn vào mạng trước Ci) như một nút cha trong Dàn. Kết quả là, cách tiếp cận của luận văn xây dựng hiệu quả Dàn bằng cách thiết lập mối quan hệ giữa cha - con theo cách từ dưới lên. Hai định lý sau đảm bảo tính đúng đắn của phương pháp được đề xuất.

Định lý 1: BVCL liệt kê tất cả các tập phổ biến đóng.

Chứng minh:

Giả thiết rằng một bộ các tập phổ biến đóng (FCIs), C = {C1, C2,. . . , Cm} có thể được khai thác từ cơ sở dữ liệu giao dịch với ngưỡng minSup. Một tập phổ biến đóng Ci có thể không được nằm trong C vì hai lý do:

(i) Ci đã bị cắt tỉa hoặc

(ii) Thuật toán đã chấm dứt trước khi Ci được đưa vào C.

Thuật toán thu được các FCIs bằng cách khai thác các thuộc tính (DBV) và (DSBV) của tập hạng mục. Nó khai thác các FCIs đại diện cho mỗi nhánh bằng cách khởi tạo subsuming của mỗi hạng mục. Sau đó, sẽ bắt đầu gọi đệ quy các FCIs của nhánh đó bằng cách mở rộng các FCIs đại diện (với các hạng mục của các danh sách non - subsuming tương ứng) sử dụng bổ đề 1 và bổ đề 2. Bổ đề 3 cũng đảm bảo hiệu quả của quá trình kết hợp.

Theo giả thiết chúng ta biết rằng sup(Ci) ≥ minSup và Ci không bị subsumed bởi các tập khác (Ci ∈ C). Tuy nhiên, trong cách tiếp cận được đề xuất, Ci chỉ bị cắt tỉa nếu nó không thõa độ hỗ trợ hoặc bị loại bỏ như là tập không đóng phát sinh (theo bổ đề 5), nghĩa là nếu nó là tập đóng thì nó phải nằm trong C, mâu thuẫn với giả thiết.

Hơn nữa, thuật toán chỉ kết thúc khi nó hoàn thành các FCIs cho tất cả các nhánh mà mỗi nhánh được khởi tạo bởi một FCI đại diện. Một nhánh hoàn tất quá trình của nó khi các danh sách non - subsuming của FCI của nó là rỗng. Do đó, bất kỳ tập đóng Ci ∈ C có thể không được phát hiện theo cách tiếp cận được đề xuất chỉ khi độ hỗ trợ của các tập phát sinh của nó sup (cj) nằm dưới ngưỡng minSup, mâu thuẫn với giả thiết của chúng ta.