Khai thác dàn tập phổ biến đóng sử dụng cấu trúc DSBV

52. End

53. BVCL_extend (Ck+1, nSLCk+1);

54. insertIntoLattice (Ck+1);

55. Foreach wj SLCk+1 do

56. updateDSBV (DSBVwj, DSBVCk+1);

57. End

58. If CIDCk ≠ 0 then updateDSBV (DSBVyl, DSBVCk+1);

59. End

60. l l + 1;

61. End

Có thể bạn quan tâm!

Xem toàn bộ 72 trang tài liệu này.

62. End

Đoạn 2: Mã Giả thuật toán

1. Function insertIntoLattice(C)

2. Begin

3. LN initNode(C, CIDC, DSBVC);

4. mDSBV mineMinimalDSBV (LN.DSBV);

5. S findFCS (mDSBV);

6. Foreach {s1, s2, …, sp} S do

7. childLN mapLatNode [si];

8. LN.addChild (childLN);

9. childLN.addParent (LN);

10. End

11. End

12. Function mineMinimalDSBV (DS)

13. Begin

14. bp -1;

15. ap DS.pos;

16. p 0;

17. While p |DS| do

18. If (pb ≥ 0) then

19. Xóa bit thứ bp+1 từ DS.bp

20. End

21. If DS.sbv[i] ≠ 0 then

22. Bp nzLSBTable [DS.bp];

23. CIDs compCID (bp, ap);

24. temDS mapDSBV [CIDs];

25. R compRange (DS, temDS);

26. i R.c1;

27. j R.c2;

28. for (k := 1; k ≤ R.c3; k++) do

29. DS.bi:= DS.bi ˄ temDS.bj;

30. i i + 1; j j + 1;

31. End

32. End

33. Else

34. p p + 1;

35. ap ap + 1;

36. End

37. End

38. End

39. Function findFCS ({p, {b1, b2, …, bn}})

40. Begin

41. bp -1;

42. ap p;

43. i 0;

44. While i n do

45. While bi ≠ 0 do

46. If bi chẵn then

47. Bp nzLSBTable [bi];

48. End

49. Else

50. Bp 1;

51. End

52. s computeCID(bp, ap);

53. S S s;

54. resetBit (bi, bp);

55. End

56. i i + 1;

57. ap ap + 1;

58. End

59. return S;

60. End

Đoạn 3: Mã Giả thuật toán

1. Function isClosed (DS, sup)

2. Begin

3. S findFCS (DS);

4. Foreach (si S) do

5. supsi: = compSup (DBVsi);

6. If (sup = supsi) then

7. return true;

8. End

9. End

10. Return false;

11. End

12. Function compRange (DS1, DS2)

13. Begin

14. If (DS1.p1 < DS2.p2) then

15. C1 DS2.p2 – DS1.p1;

16. C2 0;

17. End

18. Else

19. C1 0;

20. C2 DS1.p1 – DS2.p2;

21. End

22. C’ |DS1| - C1;

23. C” |DS2| - C2;

24. If C’ < C” then

25. C3 C’;

26. End

27. Else

28. C3 C”;

29. End

30. R (C1, C2, C3);

31. Return R;

32. End

33. Function updateDSBV (DS1, DS2)

34. Begin

35. R compRange (DS1, DS2);

36. i R.c1;

37. j R.c2;

38. For (k=1; k ≤ R.c3; k++) do

39. DS1.bi:= DS1.bi DS2.bj;

40. i i + 1; j j + 1;

41. End

42. u1 DS1.p1 + |DS1|;

43. u2 DS2.p2 + |DS2|;

44. If u2 u1 then

45. L R.c2 + R.c3;

46. count u2 – u1;

47. appendBytes (DS1, DS2, l, count);

48. End

49. End

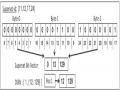
Input của thuật toán là cơ sở dữ liệu giao dịch với ngưỡng minsup. Tại dòng số 2, các hạng mục phổ biến được xác định bởi hàm findFrequentItems(). Mỗi hạng mục phổ biến xi được khởi tạo bằng cách xây dựng bit vector động (DBV) từ tidset. Ban đầu, cids là 0 và các DSBV là rỗng cho tất cả các hạng mục phổ biến. Các hạng mục phổ biến được sắp xếp theo thứ tự tăng dần của độ hỗ trợ. 2 vòng lặp thực hiện việc kết hợp các item theo thứ tự tăng dần của danh sách các hạng mục phổ biến ở dòng 4 – 9. Ở dòng 6, danh sách non - subsuming cho mỗi mục xi được biểu diễn dưới dạng nSLxi = {y1, y2,. . . , ym} được xây dựng. Sau đó, hàm BVCL_Extend () được gọi với xi và nSLxi của nó để bắt đầu quá trình khai thác các tập phổ biến đóng theo cách depth first tại dòng số 8.

BVCL_Extend () lấy hai đối số (1) Một tập phổ biến hoặc 1 tập phổ biến đóng Ck (2) danh sách non - subsuming nSLCk của nó. Nó tính tập phổ biến đóng mới Ck+1 đệ quy bằng cách nối Ck với các hạng mục của danh sách non - subsuming nSLCk của nó cho đến khi danh sách này rỗng. Để khai thác một tập đóng Ck +1, ở dòng 18. DBV và DSBV của nó được lấy từ việc giao các DBV của tập đóng Ck và mục yl ở dòng tiếp theo. Nếu sup(Ck+1) ≥ minsup dựa trên thuộc tính DBV của nó ở dòng 20-21, hàm isClosed () được gọi để kiểm tra xem nó có sản sinh các tập hợp thừa hay tập đóng bị trùng lắp. Hàm isClosed () thực hiện nhiệm vụ này thông qua việc sử dụng DSBV thu được từ việc giao các DSBVs của Ck và yl tại dòng 22. Dòng 26 - 27 gán cid mới cho Ck +1 và DSBV của mục yl được cập nhật với giá trị cid mới được gán này sử dụng hàm setBit ().

Để tính Ck+1 vòng lặp while (dòng 33–46) lặp cho các mục còn lại của danh sách non - subsuming của Ck (là nSLCk). Do đó, Ck+1 được sáp nhập với các hạng mục của nSLCk ở dòng 34. Danh sách subsuming và non - subsuming của Ck+1 cũng được tính trong quá trình subsuming tại dòng 36 và dòng 43. Danh nSLCk có thể xóa bớt dựa trên các thuộc tính khai báo như đã nêu trong bổ đề 2. Ở dòng số 38, BVCL_Extend () được gọi lại để tính các FCIs mới từ Ck +1 tại dòng 53. Ở cuối của việc khai thác các FCIs bằng cách duyệt chiều sâu trước, hàm InsertIntoLattice () được gọi để liên kết tập đóng với bao đóng tối tiểu của nó trong Dàn ở dòng số 54.

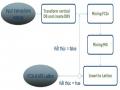
Trong đoạn 2, dòng 2-10 mô tả hàm InsertIntoLattice () để tạo lập mối quan hệ cha – con trong cấu trúc Dàn. Ở dòng 2, một node được khởi tạo với tập phổ biến đóng C. Sau đó, hàm mineMinimalDSBV() dùng DSBV của C làm input. mineMinimalDSBV() chạy vòng lặp qua tất cả các byte của DSBV của C là DS từ dòng 17-37, mỗi byte nó xác định các cid từ các bit khác 0 ở dòng 22 và 23. Nó gán cho các DSBVs (temDS) từ bảng mapDSBV (cids) {cid làm input} ở dòng 24 compRange () được gọi để tính range của các byte giữa DS và temDS ở dòng 25. Những byte (thuộc range) của DS được update sau khi giao với not (bytes của temDS) dòng 26 -31. Ở cuối của mineMinimalDSBV (), các output được cập nhật DSBV của C (DS) chỉ chứa thông tin về minimal closed supersets.

Ở dòng 5 của đoạn 2, hàm FindFCS () thực hiện cập nhật DSBV của C (mDSBV) để tìm ra tập các cids của minimal closed supersets.FindFCS () tìm byte khác 0 của DSBV. Vòng lặp for ở dòng 6 - 10 liên kết C với các si trong Dàn con. Hàm insertIntoLattice () được gọi cho mỗi tập đóng theo thứ tự depth first để xây dựng cấu trúc dàn các tập đóng.

Trong đoạn 1 dòng 55-58 bảo đảm việc truyền thông tin FCS giữa các tập đóng đã khai thác. Vòng lặp for ở dòng 55-57 cập nhật các DSBV của mỗi wi của SLCk+1 sử dụng hàm updateDSBV(). Trong đoạn 3 dòng 33-49 mô tả hàm updateDSBV(), hàm này nhận 2 DSBVs làm input, DSBV(DS1) được update bởi DSBV(DS2). Hàm compRange() được gọi để tính range của các bytes bắt đầu từ cùng vị trí của hai DSBVs. Các bytes của DS1 được update ở dòng 38-41. Các byte còn lại của DS2 được kết hợp vào DS1 được thể hiện ở dòng 42-48. ở dòng 4-8 đoạn 1, cuối vòng lặp for, thuật toán BVCL kết thúc sau khi khai thác tất các các FCIs và thiết lập các mối quan hệ của chúng trong Dàn.

4. Cải tiến thuật toán gốc

Tập đóng và tập sinh (generator) của chúng đều đóng vai trò hết sức quan trọng trong việc khai tác tập phổ biến và tập luật kết hợp. Trong phần này, luận văn trình bày một hướng tiếp cận để khai thác đồng thời tập sinh trong khi khai thác Dàn các tập phổ biến đóng đã trình bày phía trên.

4.1 Cơ sở lý thuyết

4.1.1 Kết nối Galois

Cho quan hệ hai ngôi δ I T chứa CSDL cần khai thác. Đặt: X I và Y T. Với P(S) gồm tất cả các tập con của S. Ta định nghĩa hai ánh xạ giữa P(I) và P(T) được gọi là kết nối Galois như sau:

a. t : P(I ) P(T), t(X ) yT | xX, xy.

b. i : P(T) P(I ), i(Y) xI | y Y, xy.

4.1.2 Định nghĩa toán tử đóng

 Ánh xạ (1): t(X) lấy tất cả tid của giao tác có chứa tập hạng mục X.

 Ánh xạ (2): i(Y) lấy tất cả item tồn tại trong tất cả giao tác Y. Toán tử đóng c = i ◦ t

4.1.3 Các tính chất của IT-pair

Kí hiệu itemset X và tập các giao dịch tương ứng với nó t(X) là: X x T (X ) và được gọi là IT-pair.

Cho Xi x T (Xi) và Xj x T (Xj) là hai IT-pair.Ta có 4 tính chất sau:

1. Nếu T (Xi) = T (Xj) thì c (Xi) = c (Xj) = c (Xi U Xj)

2. Nếu T (Xi) T (Xj) thì c (Xi) ≠ c (Xj) nhưng c (Xi) = c (Xi U Xj)

3. Nếu T (Xi) T (Xj) thì c (Xi) ≠ c (Xj) nhưng c (Xj) = c (Xi U Xj)

4. Nếu {T(Xi) ⊈ T(Xj)

T(Xi) ⊉ T(Xj)

thì c (Xi) ≠ c (Xj) ≠ c (Xi U Xj)

4.1.4 Minimal Generator (mG)

Cho X là tập đóng. Ta nói itemset X ' là một generator của X khi và chỉ khi:

1.X ' ⊆ X

2.Sup(X ' ) = Sup(X)

Gọi G(X) là tập các generator của X. Ta nói rằng X’ ∈ G(X) là một mG nếu nó không có tập con trong G(X). Đặt Gmin(X) là tập tất cả các mG của X. Theo định nghĩa, Gmin(X) ≠

∅ vì nếu nó không có generator hoàn toàn thì chính X là mG.

4.1.5 Một số nhận xét về mG

1. mG của 1-itemset là chính nó.

2. Trong quá trình áp dụng thuật toán tìm tập phổ biến đóng, nếu thỏa tính chất 1 thì:

mG (Xi U Xj) = mG (Xi) + mG (Xj).

3. Nếu thỏa tính chất 2 thì mG (Xi U Xj) = mG (Xi).

4. Nếu thỏa tính chất 3 thì mG (Xi U Xj) = mG (Xj).

5. Nếu thỏa tính chất 4 thì mG (Xi U Xj) = U [mG(Xi), mG(Xj)] Chứng minh [2]

4.2 Thuật toán

FindMG()

{

if SLCk+1 rỗng then

MGCk+1= ComputeMG(Ck,pI);

else

khởi tạo danh sách pMG làm input. for each p in SLCk+1

pMG <-- p

CreateMG_Ck1(Ck1,pMG);

end

}

// Tính MG cho Ck1

//pMG là con trỏ đến danh sách các phần tử làm Input cho việc tính

CreateMG_Ck1(Ck1, pMG)

{

khởi tạo danh sách pExtend để gọi đệ qui.

for each pMG do

{

-khởi tạo phần tử Uni cho danh sách pExtend.

-DBVUni = DBVpMGi ∩ DBVpMGj (với j > i)

-ItemsetUni = ItemsetpMGi U ItemsetpMGj (với j > i)

-listMGUni = ComputeMG(pMGi,pMGj);(với j > i)

-pExtend <- Uni

}

if pExtend.size == 1 then listMGCk1 <- listMGpMG1

else

CreateMG_Ck1(Ck1,pExtend);// gọi đệ qui.

end

}

///// Tính Minimal Generator của 1 Phần tử BVCL//////

//X: phần tử cần tính MG

//Y: phần tử kết hợp.(input cho việc tính MG đối với X).

ComputeMG(X,Y)

{

k=SubsumeChecking(DBVX,DBVY);

if X Y then // tính chất 2 MG = MGX

else if Y X then // tính chất 3 MG = MGY

else if X == Y then //tính chất 1 MG = MGX + MGY // tính chất 4

else MG = U(MGX,MGY)

end return MG

}

Ở mỗi lần tìm được Ck+1 trong lần gọi đệ qui cho nSLCk+1. Ta kích hoạt thuật toán tìm MG cho Ck+1. Thuật toán tìm MG cho Ck+1 gồm các bước sau:

Bước 1: Nếu danh sách subsume list của Ck+1 rỗng, ta tính MG của Ck+1 theo các tính chất của IT-pair. Ngược lại, tạo danh sách các ứng viên MG cho Ck+1 rồi gọi hàm đệ qui tạo MG từ danh sách ứng viên.