Đặc Tả Và Phân Tích Thuật Toán Input: Csdl Giao Dịch: Db, Minsup.

Định lý 2: BVCL xây dựng hoàn thiện Dàn các tập phổ biến đóng.

Chứng minh:

BVCL khởi tạo quá trình đệ quy để khai thác các tập đóng sau khi tìm ra các tập đóng đại diện thông qua quá trình xử lý subsuming. Nó phát sinh tập tất cả các tập đóng C bằng cách mở rộng các FCIs đại diện với các hạng mục trong các danh sách non - subsuming tương ứng của chúng. Các hạng mục của danh sách non - subsuming không được sắp xếp dựa trên độ hỗ trợ và các tập đóng được liệt kê dùng chiến lược depth first.

BVCL thiết lập mối quan hệ cha – con bằng cách xem xét tất cả các tập đóng theo trật tự hàng ngang. Nó bảo đảm rằng với bất kỳ hai tập đóng Ci và Cj, nếu Ci ⊂ Cj, thì Cj được chèn vào Dàn như là một nút mới Nj trước Ni. Ngược lại, trong quá trình chèn Ci như là một nút mới Ni vào Dàn L, Ni được liên kết với Nj trực tiếp bằng cách thỏa Ci = bao đóng tối tiểu(Cj) hoặc gián tiếp qua một nút Nk (đã được chèn vào L) bằng cách thõa Ci ⊂ Cj = bao đóng tối tiểu (Ck), trong đó Ck ∈ Nk. Như vậy, BVCL thành công xây dựng cấu trúc Dàn các tập phổ biến đóng theo cách từ dưới lên bằng cách duy trì mối quan hệ cha - con cho mỗi cặp FCIs trong Dàn.

2.1 Lưu đồ tổng quát của thuật toán

Quá trình tổng quát của BVCL được thể hiện trong Hình 2.2 sử dụng sơ đồ khối. Luận văn cũng minh họa cách tiếp cận sử dụng cơ sở dữ liệu book - store mẫu trong Bảng 2.1 để khai thác Dàn FCIs theo các bước sau:

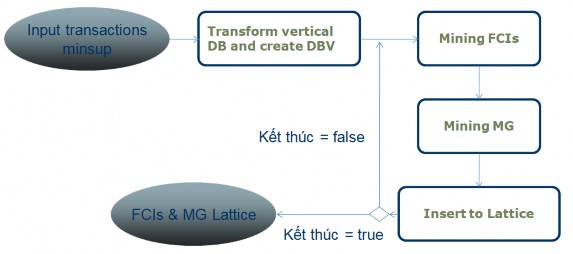
Hình 3.1: Lưu đồ thuật toán

2.2 Các bước chính của thuật toán Bước 1:

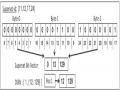
Các Item phổ biến của danh sách L được sắp tăng dần theo độ phổ biến. với minsup = 30%, L ={“A”,“C”,“M”, “D”,“P”,“N”,“L”}. Bảng 2.3 trình bày DBV và DSBV của

các Item phổ biến. DBV được xây dựng trực tiếp từ tidset và DSBV rỗng ở giai đoạn ban đầu.

Bước 2:

Cho mỗi Item phổ biến xi, danh sách non-subsuming nSLxi được khởi tạo với các hạng mục xj, sao cho (xi, xj) ∈ L, sup (xj) ≥ sup (xi) và xj không bị Subsume bởi xi (thông qua việc áp dụng bổ đề 1). Nếu xi và xj subsume lẫn nhau theo bổ đề 2 (ii), xj sẽ được bỏ qua trong danh sách L. Ví dụ: Danh sách subsuming và non-subsuming của “A” là SL“A"

= {“P”, “N”, “L”} và nSL“A" = {“CM”, “D”}. Tiếp theo, "A" được kết hợp với các mục của SL"A" xuất phát từ tập đóng thứ nhất "APNL". Các danh sách subsuming và non - subsuming được xây dựng cho tất cả các hạng mục phổ biến theo cách tương tự. Trong quá trình này danh sách hạng mục phổ biến là: L= {“A”, “CM”, “D”, “P”, “N”, “L”}.

A: SL = {P, N, L}; nSL = {CM, D}

CM: SL = {L}; nSL = {D, P, N}

D: SL = {N, L}; nSL = {P}

P: SL = {L}; nSL = {N}

N: SL = {L}; nSL = {}

L: SL = {}; nSL = {}

Bước 3:

Để tiếp tục khai thác depth first các FCIs, các tập đóng mới phát hiện được mở rộng. Quá trình bắt đầu bằng cách khởi tạo danh sách nSLCk của Ck. Nếu nSLCk rỗng, chúng ta cần phải nhảy đến bước 5. Ở đây tập đóng đại diện “APNL” được mở rộng với các hạng mục của nSL“APNL" để bắt đầu đệ quy đến các FCIs trong 1 nhánh nơi mà nSL“APNL" thu được trực tiếp từ nSL"A".

Bước 4.1:

Một tập mới Ck+1 được hình thành từ việc kết hợp Ck với một hạng mục của nSLCk. Độ phổ biến của nó được kiểm tra so với ngưỡng minSup sau khi xác định DBVCk+1. Nếu sup (Ck+1) < minSup, Ck+1 được loại bỏ và Ck được kết hợp với hạng mục kế tiếp của nSLCk. Sau đó độ phổ biến được kiểm tra theo cách tương tự. Nếu không còn hạng mục trong nSLCk, thì nhảy đến bước 5. Trong database của ví dụ này, “APNL” kết hợp với “CM ” ∈ nSL“APNL " để xây dựng Ck+1 = “APNL”  “CM ”= “APNLCM”. Tiếp theo, dynamic bit vector của “APNLCM” được xác định là DBV“APNLCM" = DBV“APNL" ∩ DBV“CM" = DBV“APNL" ∩ DBV“C" = {0, {29}} ∩ {0, {58}} = {0, {24}}.

Bước 4.2:

DSBV của Ck+1 được khai thác từ việc Giao các DSBVs của Ck và kết hợp với hạng mục y từ nSLCk theo cách trong phần 5.2.3. Tuy nhiên, nếu Ck+1 được xác nhận là một phát sinh của tập không đóng hoặc các tập trùng lắp sử dụng bổ đề 5 thông qua cấu trúc DSBV, loại bỏ nó và quay trở lại bước 4.1. Do đó DSBV “APNLCM " được khai thác bởi: DSBV“APNLCM " = DSBV“APNL " ∩ DSBV“CM " = {} ∩ {} = {}.

Bước 4.3:

Quá trình subsuming được thực hiện cho Ck+1 với các hạng mục còn lại của nSLCk. Kết quả là các danh sách subsuming và non - subsuming của Ck +1 được biểu diễn (SLCk

+1) và (nSLCk +1) được xây dựng. DSBV của Ck +1 được khởi tạo và sau đó nó được cập nhật thông qua giao DSBV của các hạng mục từ SLCk +1. Trong suốt quá trình subsuming, trong database của ví dụ này. Tập hạng mục “APNLCM” không bị subsumed bởi các item còn lại của nSL“APNL" = {“D”}. Do đó, "APNLCM" được coi là FCI thứ hai và nSL"APNLCM" được khởi tạo là {"D"}.

Bước 4.4:

Nếu nSLCk +1 khác rỗng, có thể mở rộng Ck+1. Để phát hiện các FCIs con cháu của cây khai thác FCI, chuyển sang bước 3 và lặp lại các bước trên. Ở đây, nSL“APNLCM " ≠  và chúng ta thu được 1 tập mới “APNLCMD”. Tuy nhiên, quan sát thấy rằng sup ("APNLCMD") (tính từ DBV"APNLCMD") nằm dưới ngưỡng minSup, trong đó DBV"APNLCMD" = DBV"APNLCM" ∩ DBV"D" = {0, {24}} ∩ {0, {53}} = {0, {16}}.

"APNLCMD" bị loại bỏ như một tập không phổ biến như trong hình 3.2.

Tập đóng

CML {D, P, N}

{ P } PL { N } NL



DNL

{ }

CMLN

{}

DNLP

{}

PNL

{}

APNL

{CM, D}

APNLCM

{D}

Tập Không phổ biến Tập Không đóng

APNLD

{}

CMLDN

{P}

CMLP

{N}

Có thể bạn quan tâm!

Xem toàn bộ 72 trang tài liệu này.

{}

APNLCMD

CMLDNP

CMLPN

Hình 3.2: Cây khai thác FCIs

Bước 5:

Tập các bao đóng phổ biến tối tiểu được xác định cho một tập đóng C từ cấu trúc DSBV của nó bằng cách áp dụng các chiến lược thảo luận trong phần 5.2.1. C được liên kết với các bao đóng tối tiểu như một nút cha trong Dàn. Do không còn FCI mới nào có thể được khai thác từ “APNLCM” và cũng không còn bao đóng của “APNLCM”. Do đó "APNLCM" được chèn vào Dàn như một nút đầu tiên (hình 3.3).

Bước 6:

Để truyền thông tin bao đóng lên phía các FCIs được khai thác, cho đến thời điểm này, mọi tập phổ biến đóng Ck+1 đều cập nhật DSBV về việc thu thập các tập đóng Ck bằng DSBV riêng của nó. Nó cũng phải cập nhật DSBV cho các hạng mục của SLCk.

Bước 7:

Nhảy đến bước 3 và lặp lại các bước trên để hoàn tất việc lấy tất cả các tập đóng cho tất cả các nhánh. Xem xét mỗi tập đóng của cây khai thác FCI theo thứ tự ngang để xác định mối quan hệ giữa cha và con của Dàn các tập đóng theo cách từ dưới lên. Quay trở lại bước 3 và mô phỏng các bước trên bằng cách sử dụng ví dụ hiện tại như sau:

"APNL" được kết hợp với mục thứ hai ("D") của nSL"APNL" cho ra “APNLD”. DBV và DSBV của nó được xác định bằng DBV"APNLD" = DBV"APNL" ∩ DBVD = {0, {29}} ∩

{0, {53}} = {0, {21}} và DSBV"APNLD" = . "APNLD" được chèn vào Dàn làm nút thứ hai và nhánh bắt đầu với "APNL" cũng sẽ kết thúc vì không còn hạng mục nào trong nSL"APNL". Các tập hợp đóng "APNLD" và "APNLCM" được xác định từ "APNL" của DSBV là các bao đóng tối tiểu của "APNL" theo các chiến lược đã được định nghĩa. Sau đó, "APNL" được liên kết với các nút có chứa các bao đóng tối tiểu này trong Dàn như minh họa trong bước 5.

Tương tự, tập đóng "CML" được khai thác bằng cách subsuming "CM" với "L" và danh sách non - subsuming của nó, nSL"CML" = {"D", "P", "N"} được xác định. "CMLDN" được khai thác từ "CML" theo cách đệ quy. Không thể mở rộng "CMLDN" với mục "P" ∈ nSIL"CMLDN" bởi vì độ hỗ trợ của "CMLDNP" nằm dưới minSup và

"CMLDN" được chèn vào Dàn. Tuy nhiên, "CMLP" được khai thác như một tập phổ biến đóng với DSBV tương ứng là DSBV"CMLP" = DSBV"CML" ∩ DSBV"P" = {0, {24}} ∩

{0, {53}} = {0, {16}} và nó được coi là đóng bởi vì sup(“CMLP”) ≠ sup(“APNLCM”), với “APNLCM” là tập bao của “CMLP”.

Mặc dù, tập phổ biến "CMLPN" được lấy từ việc mở rộng "CMLP" với "N", nó được coi là một tập không đóng vì "APNLCM" là tập bao của "CMLPN" mà sup ("CMLPN" )

= sup ("APNLCM"). Vì vậy, "CMLPN" bị loại bỏ như là một tập không đóng từ cây khai thác FCI (minh họa trong hình 3.2).

Một FCI khác là "CMLN", được phát hiện từ "CML" sau khi khai thác DBV“CMLN " và DSBV“CMLN". Trong khi chèn "CMLDN", "CMLP" và "CMLN" vào Dàn, chỉ "CMLN" được liên kết với "CMLDN" như một nút cha. Sau đó "CML" được đưa vào Dàn như một nút cha cho cả hai nút "CMLP" và "CMLN" bởi vì "CMLP" và "CMLN" được xác định là các bao đóng tối tiểu của“CML” bằng các chiến lược được mô tả trong Phần 5.2.2.

Các tập đóng còn lại "DNL", "PL", "NL" và "L" được khai thác và do đó được chèn vào Dàn bằng cách duy trì quan hệ cha - con phù hợp theo hướng từ dưới lên.

Bước 8:

Output là các FCIs với Dàn của nó là L và thoát. Hình 3.2 minh họa việc khai thác tất cả các tập phổ biến đóng và Hình 3.3 cho thấy tất cả các bước trung gian của việc thiết lập các mối quan hệ giữa các tập đóng trong Dàn.

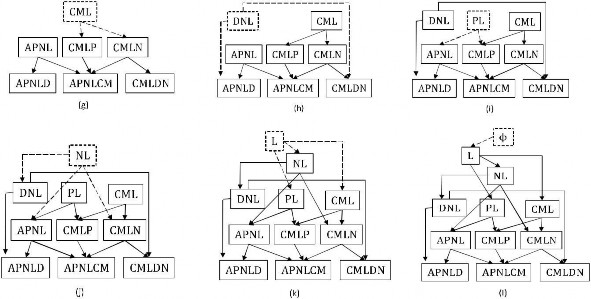
Hình 3.3: Khai thác Dàn FCIs

3. Đặc tả và phân tích thuật toán Input: CSDL giao dịch: DB, minsup.

Output: Dàn các FCIs: L

Đoạn 1: Mã Giả thuật toán

1. Begin

2. {x1, x2, …, xm} findFrequentItems ();

3. Initialize ({x1, x2, …, xm})

4. Foreach xi of {x1, x2, …, xm} do

5. Foreach xj {x1, x2, …, xm} với xi ≤ xj do

6. nSLxi: = nSLxi xj;

7. End

8. BVCL_extend (xi, nSLxi);

9. End

10. End

11. Function BVCL_extend (Ck, {y1, y2, …, ym})

12. Begin

13. l 1;

14. While l ≤ m do

15. end 1;

16. Ck+1 Ck;

17. If (CIDCk ≠ 0) then

18. Ck+1 Ck+1 yl;

19. DBVCk+1:= DBVCk DBVyl;

20. supCk+1:= compSupport (DBVCk+1);

21. If supCk+1 ≥ minsup then

22. DSBVCk+1 := DSBVCk DSBVyl

23. If isClosed (DSBVCk+1, supCk+1) then

24. end 0;

25. l l + 1;

26. CIDCk+1 assignCID ();

27. setBit (DSBVyl, CIDCk+1);

28. End

29. End

30. End

31. If (end = 0 or CIDCk = 0) then

32. j l;

33. While j ≤ m do

34. If isSubsumedBy (DBVCk+1, DBVyj) then

35. Ck+1 Ck+1 yj;

36. SLCk+1 SLCk+1 yj;

37. DSBVCk+1:= DSBVCk+1 DSBVyj;

38. If isSubsumedBy (DBVyj, DBVCk+1) then

39. Xóa yj từ {y1, y2, …, ym};

40. End

41. End

42. Else

43. nSLCk+1 nSLCk+1 yj;

44. End

45. j j + 1;

46. End

47. If CIDCk ≠ 0 then

48. CIDCk+1 assignCID ();

49. End

50. Foreach wj SLCk+1 do

51. setBit (DSBVwj, CIDCk+1);