Index-BitTableFI [25] sử dụng biểu diễn bit - vector để bổ sung các tập thừa. Tuy nhiên, một lượng đáng kể không gian vẫn bị lãng phí cho một tập phổ biến, bởi vì kích thước của một vector - bit luôn bằng với tổng số các giao dịch.
DBV-Miner [6] đề xuất 1 giải pháp sử dụng cấu trúc dữ liệu gọi là Dynamic Bit- Vector (DBV). Nó xóa những bit 0 bắt đầu trong bit - vector và theo dõi các vị trí khác 0 bắt gặp dầu tiên. Do đó, DBV kết hợp với một lookup table, thuận tiện cho quá trình tính toán độ support của tập dữ liệu. Lookup table lưu trữ tổng số bit 1 cho mỗi kết hợp của 8-bit trong một byte. Nó tính độ Support của 1 tập X bằng cách tính tổng các số 1 cho mỗi byte bi của DBVX:
𝑆𝑢𝑝(𝑋) = ∑ 𝐿𝑜𝑜𝑘𝑢𝑝(𝑏𝑖 )
𝑏𝑖∈𝐷𝐵𝑉𝑋
Bảng 2.3 cho thấy cách biểu diễn cơ sở dữ liệu theo chiều dọc của Bảng 2.1 theo bit vector.
Bảng 2.3: Cơ sở dữ liệu giao dịch theo chiều dọc dùng bit vector.
Tidset | Bit- vector | DBV | |
A | t1, t3, t4, t5 | 011101 | {0,29} |
L | t1, t2, t3, t4, t5, t6 | 111111 | {0,63} |
C | t2, t4, t5, t6 | 111010 | {0,58} |
D | t1, t3, t5, t6 | 110101 | {0,53} |
P | t1, t2, t3, t4, t5 | 011111 | {0,31} |
M | t2, t4, t5, t6 | 111010 | {0,58} |
N | t1, t3, t4, t5, t6 | 111101 | {0,61} |
Có thể bạn quan tâm!
-
Khai thác dàn tập phổ biến đóng sử dụng cấu trúc DSBV - 1 -
Khai thác dàn tập phổ biến đóng sử dụng cấu trúc DSBV - 2 -
Phương Pháp Nghiên Cứu Và Đối Tượng Nghiên Cứu -
Đề Xuất Thuật Toán Khai Thác Dàn Các Tập Phổ Biến Đóng Và Cải Tiến -
Đặc Tả Và Phân Tích Thuật Toán Input: Csdl Giao Dịch: Db, Minsup. -
Khai thác dàn tập phổ biến đóng sử dụng cấu trúc DSBV - 7
Xem toàn bộ 72 trang tài liệu này.
DBV - Miner xây dựng một DBV mới bằng cách giao hai DBVs thông qua phép toán AND theo bit. Dựa trên phép giao này, quan hệ tập con giữa các DBVs cũng được xác định:
Xét 2 DBVs là: DBVX and DBVY.
DBVX được gọi là tập con của DBVY nếu: 𝐷𝐵𝑉𝑋 = 𝐷𝐵𝑉𝑋 ∩ 𝐷𝐵𝑉𝑌
DBVX được gọi là bằng DBVY nếu: 𝐷𝐵𝑉𝑋 = 𝐷𝐵𝑉𝑋 ∩ 𝐷𝐵𝑉𝑌 = 𝐷𝐵𝑉𝑌
Để tăng tốc độ quá trình khai thác của FCI, DBV - Miner làm giảm không gian tìm kiếm bằng cách loại bỏ việc phát sinh các tập dư thừa. Các phát sinh tập dư thừa này được loại bỏ dựa trên các thuộc tính subsume được xác định trong bổ đề 1 và bổ đề 2.
Subsume: Tạm gọi là hấp thụ
Bổ đề 1: xét 2 DBVs, DBVX và DBVY, nếu DBVX ⊆ DBVY, thì X bị subsumed bởi Y.
Bổ đề 2:
i. Nếu X bị subsumed bởi Y, thì X không phải là 1 tập đóng.
ii. Nếu X bị subsumed bởi Y, và Y bị subsumed bởi X, thì X và Y không phải là tập đóng.
Tóm tắt: một tập X dư thừa đối với tập Y, nếu DBVX ⊆ DBVY theo bổ đề 1. Do đó, X và Y được hợp nhất với nhau để xây dựng tập Z mới. Hơn nữa, X được coi là một tập không đóng nếu điều kiện của bổ đề 2 (i) được thỏa mãn, cả X và Y đều bị loại bỏ như các tập không đóng theo điều kiện được ghi trong bổ đề 2 (ii).
A sliding window model [26] giới thiệu nhiều cấu trúc dữ liệu để lưu trữ cơ sở dữ liệu giao dịch tốn ít không gian nhất khi khai thác các tập phổ biến đóng.
[27] đã đề xuất một cách tiếp cận cải tiến để khai thác các tập phổ biến đóng. Nó duy trì một tập tạm thời cho FCI đang được khai thác và cập nhật các thiết lập bất cứ khi nào một giao dịch mới được thêm vào hoặc xóa khỏi cơ sở dữ liệu giao dịch ban đầu. Tuy nhiên, tất cả các phương pháp này phát hiện FCIs từ cơ sở dữ liệu có thể được tự động mở rộng hoặc thu nhỏ bất cứ lúc nào.
GENCLOSE [5] khai thác các FCI (đồng thời phát sinh) từ CSDL tỉnh thông qua 3 phương thức mở rộng của họ.
MMCAR [17] đã thiết kế việc khai thác các FCI ở mức độ phân cấp vào năm 2014.
Cách tiếp cận khai thác FCI gần đây.
NAFCP [28] đã đề xuất phương pháp dựa trên cấu trúc N-List và cây PPC. NList
[29] là một cấu trúc theo chiều dọc có thể được sử dụng hiệu quả trong việc tính toán độ hỗ trợ của các tập phổ biến. PPC-tree [29] tương tự như FP - Tree lưu trữ toàn bộ cơ sở dữ liệu trong bộ nhớ bằng cách sử dụng Nodes, mỗi Node lưu trữ thông tin cần thiết của mẫu phổ biến. NAFCP xây dựng N-List cho mỗi mẫu phổ biến từ PPC-Tree. Tuy nhiên, NAFCP cần phải áp dụng cơ chế kiểm tra Subsume để loại bỏ các tập không đóng.
3. Hướng tiếp cận khai thác tập sinh (Minimal Generator)
Hiện nay, việc tìm tập sinh của tập phổ biến đóng đều dựa vào thuật toán Apriori. Phương pháp thứ nhất được trình bày bởi Bastide và đồng sự, các tác giả đã mở rộng thuật toán Apriori để tìm mG. Đầu tiên thuật toán tìm các ứng viên là các mG, sau đó nó tính bao đóng của chúng để tìm tập đóng.
Phương pháp thứ hai được trình bày bởi Zaki. Đầu tiên, tác giả dùng thuật toán CHARM để tìm tất cả các tập đóng. Sau đó, ứng với mỗi tập đóng tác giả sử dụng phương pháp Apriori để tìm tất cả các mG của nó.
Cả hai phương pháp này đều gặp bất lợi khi kích thước của tập phổ biến lớn bởi vì số lượng tập ứng viên cần xét rất lớn.
Tiếp theo là thuật toán tìm nhanh tập sinh [2]. Nó khắc phục nhược điểm của hai phương pháp trên bằng cách dựa vào thuật toán không sinh ứng viên (CHARM) để sinh tập phổ biến đóng và đồng thời cũng tìm luôn mG của chúng.
4. Hướng tiếp cận khai thác Dàn các tập phổ biến đóng
Cấu trúc Dàn diễn đạt mối quan hê Cha - Con giữa các FCIs. Đối với mỗi cặp Nodes chứa các tập đóng. Khai thác thuộc tính này của 1 cấu trúc Dàn, có thể rút ra các luật kết hợp có ý nghĩa từ Dàn trong một thời gian rất ngắn [4]. Tiếc rằng, có rất ít công trình nghiên cứu tính toán cấu trúc Dàn của các tập phổ biến đóng cũng như quá trình khai thác các tập đóng. Phương pháp tiếp cận naïve để tính toán cấu trúc Dàn các
tập đóng rất tốn kém vì nó đòi hỏi phải tìm kiếm vét cạn để tìm ra các tập Cha nhỏ nhất cho mỗi FCI, với tổng chi phí O(C2), với C là tập đóng.
DCHARM-L [8] khởi xướng cho việc xuất Dàn trong khi khai thác các FCIs ở thời gian chạy. Tuy nhiên, nó đòi hỏi phải điều chỉnh lại mối quan hệ được xây dựng trước đó trong các tập đóng sau khi chèn tập đóng mới vào Dàn.
DÀN TẬP ĐÓNG [7] đã đưa ra phương pháp để xây dựng FCIL trực tiếp từ danh sách các FCIs trong giai đoạn xử lý sau của phương pháp khai thác FCI. Tuy nhiên, hiệu suất tính toán offline này cũng chưa tối ưu. Chiến lược này xem như phương pháp khai thác Dàn offline.
5. Đề xuất cấu trúc dữ liệu
Mục đích của đề tài là khai thác đồng thời FCI và cấu trúc Dàn, phát triển một cấu trúc dữ liệu để:
(1) Loại bỏ việc phát sinh các tập không đóng.
(2) Lưu giữ thông tin của bao phổ biến đóng (FCS) ,
(3) Duy trì mối quan hệ cha - con giữa các tập phổ biến đóng.
Hơn nữa, cấu trúc dữ liệu được đề xuất cũng đảm bảo truy xuất nhanh, cập nhật và xóa thông tin của FCS cho một tập. Trong phần này, giới thiệu Superset Bit-Vector và sau đó mở rộng nó sang dạng nâng cao hơn gọi là Dynamic Superset Bit-Vector (DSBV).
5.1 Superset bit-vector
Superset Bit - Vector lưu trữ thông tin cho FCS của 1 tập sử dụng chuỗi bit. Trong phương pháp này, mọi FCI được xác định bởi một định danh duy nhất được gọi là closed itemset identifier (cid). Không giống như bit - vector là biểu diễn cho Tidset, mỗi bit của superset bit-vector tương ứng với một cid của một FCI. Cho X là một tập hạng mục có một tập các FCS mà các mã cids của nó được liệt kê trong {11, 12, 17, 24}.
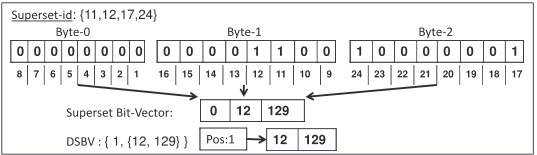
Hình 2.1: Dynamic superset bit vector
Chú ý rằng vị trí 11, 12, 17 và 21 trong chuỗi bit được set 1. Do đó, superset bit - vector của X được biểu diễn bằng một tập các byte {0, 12, 129}, trong đó mỗi byte được biểu diễn dưới dạng giá trị thập phân.
Superset bit - vector có thể chứa nhiều bit 0 nên tốn không gian lưu trữ. Do đó, một dạng mở rộng của superset bit-vector được gọi là Dynamic Superset Bit Vector (DSBV) được đề xuất để lưu trữ thông tin FCS với bộ nhớ tối ưu.
5.2 Dynamic superset bit-vector
Cấu trúc của dynamic superset bit vector:
typedef struct DBV
{
public:
int iNonZeroByte;// vị trí của byte khác 0 đầu tiên.
// các byte lưu bit vector bỏ các byte zero đầu và cuối. vector<unsigned char> bitVec;
DBV()//khởi tạo cho struct
{
iNonZeroByte=-1;
}
}DBV;
Dynamic Superset Bit Vector (DSBV) bao gồm 2 thành phần, nó được biểu diễn dưới dạng {p, {b1, b2,. . . , bn}} trong đó phần thứ nhất p theo dõi vị trí của byte khác
0 đầu tiên của superset bit-vector, thành phần thứ 2 {b1, b2,. . . , bn} biểu diễn cho một danh sách các byte trong superset bit - vector sau khi loại bỏ các byte zero đầu và cuối. Như vậy thông tin FCS của X được thể hiện trong DSBV dưới dạng {1, {12, 129}}. (p=1 bởi vì byte thứ 1 khác 0)
DSBV đóng một vai trò quan trọng trong việc xây dựng cấu trúc Dàn các tập phổ biến đóng. Trong Dàn chỉ có các minimal closed supersets (bao đóng tối tiểu) có thể là nút con của FCI. Khai thác tính chất này của Dàn, chúng ta bắt đầu thiết lập mối quan hệ cha – con giữa các tập đóng theo hướng từ dưới lên. Sau đây là các chiến lược tìm kiếm, xóa và cập nhật thông tin FCS của các tập.
5.2.1 Tìm FCS từ cấu trúc DSBV
nzLSB: non-zero least significant bit ( vị trí bit 1 gần nhất trong byte tính từ phải qua)
Thông tin FCS của 1 tập hạng mục được lấy từ các thuộc tính DSBV của nó. Tập của các closed supersets với các Cids tương ứng nhanh chóng được xác định từ DSBV của nó. Xem xét DSBV của một tập hạng mục X, dX = {p, {b1, b2, . . . , bn}}
- Giả sử vị trí thực của một byte bi được ký hiệu bởi ap và
- nzLSBc: là vị trí bit 1 tương ứng với byte bi.
- Sj là cid: Sj = 8 * ap + nzLSBc.
Bảng 2.4 mô tả quá trình xác định FCS (cid) của một tập hạng mục có DSBV {1,
{12, 129}} (từ DSBV của tập hạng mục X, ta có thể tìm tập các FCS của X như bên dưới
Bảng 2.4: Tìm cids của FCS của itemset có DSBV: {1, {12, 129}}
Actual position | Byte | Status | nzLSB | cid | Set of FCS | After reset | |
[i] | ap | bi | nzLSBc | sj | S | bi | |
0 | 1 | 12 | Even | 3 | 11 | {11} | 8 |
1 | 8 | Even | 4 | 12 | {11,12} | 0 | |
1 | 2 | 129 | Odd | 1 | 17 | {11,12,17} | 128 |
2 | 128 | Even | 8 | 24 | {11,12,17,24} | 0 |
5.2.2 Tìm minimal FCS từ cấu trúc DSBV
Phương pháp khai thác hiệu quả để trích xuất thông tin FCS tối tiểu từ cấu trúc DSBV. Xét 1 FCI là C, DSBV của nó là dC = {p1, {b1, b2, . . . ,bn}}. Giả sử tập cids của FCS là S = { s1, s2, . . . , sm } của C có được từ dC bằng giải thuật mô tả trong phần
4.2.1 phía trên. Với mỗi Si, bộ thông tin của FCS là Ri = {r1, r2 , . . . , rm } được lấy từ DSBVsi. Sau đó, lấy S = S – Ri để xóa các tập chung trong cả S và R. Do đó, sau quá trình lặp cho tất cả các Ri, S chỉ chứa các cids của minimal closed supersets của C. (Bởi vì 1 tập mà là superset 2 lần thì nó không phải là minimal superset)
Bảng 2.5 minh họa một ví dụ về khai thác minimal FCS từ 1 DSBV d = {1, {134, 129}}.
Sd = {10, 11, 16, 17, 24} được xác định từ d. Sau đó, DSBV d ’= {1, {4, 1}} cho FCS của cid =10 được lấy từ cột “mapping” của bảng 2.5.
Sau khi xác định tập Sd’ = {11, 17} từ d’. Thực hiện Sd = Sd - Sd’. Làm tương tự sau khi cập nhật Sd = {10, 16, 24}. Lúc này, tập của FCS (Sd’ = {24}) cho 1 tập đóng với cid = 16, kết quả cuối cùng Sd = {10, 16} mô tả cho tập các cids chỉ của minimal closed supersets.
Bảng 2.5: Khai thác minimal FCS từ cấu trúc DSBV
DSBV | Set of | cid of | DSBV of | Set of FCS | Updating of | Updating of | Mapping | ||
FCS | ith FCI | ith FCI | of ith FCI | FCS | d | ||||
i | d | Sd | cidi | d | Sd | Sd = Sd − Sd | d = d d | cid | DSBV |
1 | {1, {134, 129}} | {10,11,16,17,24} | 10 | {1, {4, 1}} | {11,17} | {10,16,24} | {1, {130, 128}} | 10 | {1, {4, 1}} |
11 | {3, {4, 8}} | ||||||||
. . . | . . . | ||||||||
2 | {1, {130, 128}} | {10,16,24} | 16 | {2, {128}} | {24} | {10,16} | {1, {130}} | . . . | . . . |
16 | {2, {128}} | ||||||||
20 | {0, {122, 23}} |
Lưu ý: cột thứ 4 ( DSBV của FCI thứ i) đã có trong quá trình xác định FCS trong chương trình.
5.2.3 Giao 2 DSBVs
Để xác định tập các FCS của một tập mới khai thác. DSBV cho một tập mới được phát hiện thu được bằng cách giao DSBV của hai FCI. Phép giao tập hợp này được thực hiện bằng phép toán AND trên bit liên tục giữa các byte của hai DSBV.
Đặc tả thuật toán bằng mã giả như sau:
DBV SetHelper::Interset2DBV(DBV* X,DBV* Y)
{
xMax=X->iNonZeroByte;//chỉ số byte cao của X
xMin=X->iNonZeroByte - X->bitVec.size()-1;//chỉ số byte thấp của X yMax=Y->iNonZeroByte;//chỉ số byte cao của Y
yMin=Y->iNonZeroByte - Y->bitVec.size()-1;//chỉ số byte thấp của Y rMax=min(xMax,yMax);//chỉ số byte cao của kết quả rMin=max(xMin,yMin);//chỉ số byte thấp của kết quả
- if(rMin>rMax) return vector 0;
-for(i=rMin to rMax) Result = X bitwise AND Y;
-Xóa byte 0 bên phải;
-xóa byte 0 bên trái; return result;
}