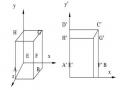
1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 0 | −1 | 0 | 0 | 0 | 1 | 0 | 0 |
= 0 | 0 | 1 | 0 ∗ | 0 | 0 | −1 | 0 | ||||
0 | −𝑡𝑦 | −𝑡𝑧 | 1 | 0 | 0 | 0 | 1 | 0 | 𝑡𝑦 | 𝑡𝑧 | 1 |
1 | 0 | 0 | 0 | ||||||||
= 0 0 0 | −1 0 2 ∗ 𝑡𝑦 | 0 −1 2 ∗ 𝑡𝑧 | 0 0 1 | ||||||||
Có thể bạn quan tâm!
-
Ảnh Của Phép Chiếu Trimetric Với Các Tham Số Góc Xoay Thay Đổi -
Phép Biến Đổi Mô Hình Và Phép Biến Đổi Hệ Trục Toạ Độ -
Đồ họa máy tính - 22 -
Phân Bố Các Điểm Trong Vùng Theo Thứ Tự Tăng Dần -
Giới Thiệu Về Các Hệ Màu Trong Màn Hình Đồ Họa -
Đồ họa máy tính - 26
Xem toàn bộ 240 trang tài liệu này.
T=T1*T2*T3
∗ 0 0 1 0
5.
1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 0 | −𝑡𝑧 | 1 |
- Bước 1: Tịnh tiến đối xứng về gốc tọa độ có ma trận là: T1=
- Bước 2: Đối xứng qua mặt phẳng (xOy) có ma trận là
1 0 0 0
0 | 0 | −1 | 0 |
0 | 0 | 0 | 1 |
T2= 0 1 0 0
1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 0 | 𝑡𝑧 | 1 |
- Bước 3: Tịnh tiến ngược về vị trí ban đầu có ma trận là T3=
- Bước 4: Ma trận của phép đối xứng qua mặt phẳng song song với mặt
phẳng xOy (yOz, zOx), cách mặt phẳng xOy (...) một khoảng tz(...) T=T1*T2*T3
1 0 0 0
=
0 1 0 0
0 0 1 0
0 0 −𝑡𝑧 1
1 0 0 0
∗ 0 1 0 0
0 0 −1 0
0 0 0 1
∗
1 0 0 0
0 1 0 0
0 0 1 0
0 0 𝑡𝑧 1
1 0 0 0
0 | 0 | −1 | 0 |
0 | 0 | 2 ∗ 𝑡𝑧 | 1 |
= 0 1 0 0
6.
- Bước 1: Quay quanh trục Oy có ma trận là
T1=
cos 𝛼 0 − sin 𝛼 0 0 1 0 0
sin 𝛼 0 cos 𝛼 0
0 0 0 1
cos 𝛽 sin 𝛽 0 0
− sin 𝛽 cos 𝛽 0 0
0 | 0 | 1 | 0 |
0 | 0 | 0 | 1 |
- Bước 2: Quay quanh trục Oz có ma trận là T2=
- Bước 3: Ma trận của phép kết hợp phép quay một góc α quanh trục Oy và phép quay một góc β quanh trục Oz là:
T=T1*T2
cos 𝛼 | 0 | − sin 𝛼 | 0 | cos 𝛽 | sin 𝛽 | 0 | 0 |
= 0 | 1 | 0 | 0 ∗ − sin 𝛽 | cos 𝛽 | 0 | 0 | |
sin 𝛼 | 0 | cos 𝛼 | 0 | 0 | 0 | 1 | 0 |
0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
cos 𝛼 ∗ cos 𝛽 | cos 𝛼 ∗ sin 𝛽 | − sin 𝛼 | 0 | ||||
= − sin 𝛽 | cos 𝛽 | 0 | 0 | ||||
sin 𝛼 ∗ cos 𝛽 sin 𝛼 ∗ sin 𝛽 cos 𝛼 0 0 0 0 1
7.
1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 |
0 | 0 | 1 | 0 |
𝑡𝑥 | 𝑡𝑦 | 𝑡𝑧 | 1 |
- Bước 1: Tịnh tiến (tx, ty, tz) về gốc tọa độ có ma trận là:
T1=
1 | 0 | 0 | 0 |
0 cos 𝛼 sin 𝛼 0 | |||
0 | − sin 𝛼 | cos 𝛼 | 0 |
0 | 0 | 0 | 1 |
- Bước 2: Quay quanh trục Ox có ma trận là T2=
cos 𝛽 0 − sin 𝛽 0
- Bước 3: Quay quanh trục Oy có ma trận là T3=
0 1 0 0
sin 𝛽 0 cos 𝛽 0
0 0 0 1
- Bước 4: Ma trận của kết hợp phép tịnh tiến (tx, ty, tz) với phép quay quanh trục Ox một góc α và quay quanh trục Oy một góc β là:
T=T1*T2*T3
1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | cos 𝛽 | 0 | − sin 𝛽 | 0 |
0 | 1 | 0 | 0 | ||||||||
0 | 0 | 1 | 0 ∗ | − sin 𝛼 | cos 𝛼 | 0 | sin 𝛽 | 0 | cos 𝛽 | 0 | |
𝑡𝑥 | 𝑡𝑦 | 𝑡𝑧 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
0 1 0 0
=
0 cos 𝛼 sin 𝛼 0 0
∗
=
cos 𝛽 0 − sin 𝛽 0
sin 𝛼 ∗ sin 𝛽 cos 𝛼 sin 𝛼 ∗ cos 𝛽 0
cos 𝛼 ∗ sin 𝛽 − sin 𝛼 cos 𝛼 ∗ sin 𝛽 0
𝑡𝑥 ∗ cos 𝛽 + (𝑡𝑦 ∗ sin 𝛼 + 𝑡𝑧 ∗ cos 𝛼) ∗ sin 𝛽 𝑡𝑦 ∗ cos 𝛼 − 𝑡𝑧 ∗ sin 𝛼 𝑡𝑥 ∗ sin 𝛽 + (𝑡𝑦 ∗ sin 𝛼 + 𝑡𝑧 ∗ cos 𝛼) ∗ cos 𝛽 1
6.1. Ánh sáng đơn sắc
Chương 6
MÀU SẮC TRONG ĐỒ HỌA
Ánh sáng đơn sắc là ánh sángmà chúng ta có thể quan sát từ hình ảnh trên tivi hay màn hình đen trắng và khi đó mắt của chúng ta không cảm nhận được các sắc màu khác như vàng, đỏ,tím…khi quan sát trên màn hình.
Định lượng là thuộc tính duy nhất của các tia sáng đơn sắc và về mặt vật lý nó được tính bằng năng lượng của tia sáng được mô tả cường độ hay độ chiếu sáng
Dưới góc độ cảm nhận về mặt tâm lý thì cường độ của tia sáng chính là độ sáng của vật (brighness)
Sử dụng phổ kế -photometer để đo độ sáng thấp nhất (min) và độ sáng cao nhất (min) của màn hình .Và đó là khoảng động
Khoảng cường độ ánh sáng nhận giá trị min là 𝐼0, đến mã là 1.0 . Làm thế nào để thể hiện được 256 mức xám khác nhau?
6.1.1. Cường độ sáng và cách tính
Khi hình ảnh xám được hiển thị trên màn hình thì cường độ của nguồn sáng sẽ thay đổi theo một thang đo với rất nhiều mức khác nhau trong khoảng từ 0 đến 1 với 0 quy ước cho màu đen,1 quy ước cho màu trắng
Giả sử muốn hiển thị trên 256 mức độ sáng khác nhau , làm thế nào để phân chia khoảng giữa các mức của cường độ sáng .
Chúng ta nhận thấy rằng khoảng thể hiện của cường độ sáng không tuyến tính với mức độ chia .
Điều đó có nghĩa khi ta chia khoảng từ 0->0.1 ra làm 128 phần thì giá trị tăng cường độ tại mỗi phần chia không bằng nhau và khác xa so với cùng số thang chia trong khoảng từ 0.9->1.
Tuy nhiên sự thay đổi trong khoảng từ 0.1->0.11 lại tương đương với khoảng từ 0.5->0.55, điều đó cho ta thấy khoảng tăng của cường độ sáng sẽ phân chia theo hàm logarit
Để có 256 mức độ sáng liên tục với giá trị mức thấp nhất là I0 và giá trị mức tối đa là 1thì các mức biến đổi tỷ lệ sẽ có giá trị r và chúng có thể rút ra bởi công thức sau:
I0 = I0 ,I1=r I0,I2=r I1 , I3=r2I0 , …, I255=r255 I0=1
r=(1/I0)1/255 Ij= I0 * rj = I0(255-j)/255
Với số khoảng phân chia của cường độ sáng tổng quát là n+1 ta có: r=(1/I0)1/n Ij= I0(n – j )/n Với j € [ 0 , n ]
Ví dụ:
Khi n=3 và 𝐼0 =1/8
r=(1/𝐼0)1/𝑛 = (1/(1/8))1/3=2 Các giá trị tương ứng
𝐼0=1/8; 𝐼1=1/4 ; 𝐼2=1/2 ; 𝐼3=1;
Thông thường giá trị I0 của màn hình CRT nằm trong khoảng từ 1/200 đến 1/40 vì độ phản xạ của màn hình phốt pho cho phép cường độ sáng đạt đến giá trị cực tiểu 0.
Tỉ số giữa giá trị lớn nhất và bé nhất của cường độ sáng đặc trưng cho mỗi loại màn hình được gọi là khoảng biến động
Việc phân chia cường độ sáng theo cách trên với màn hình CRT là cực kì phức tạp và quá trình ghi hình lên phim sẽ càng rắc rối vì tính phi tuyến tính giữa màn hình và phim.Ta đã biết cường độ trên màn CRT tỉ lệ với số lượng các hạt điện tử trong chùm tia phát ra từ cathode. Giả sử số lượng hạt tại một thời điểm phát ra là N thì công thức đo cường độ ánh sáng có dạng:
I=k. 𝑁𝛾 Với k, γ là các hằng số
Giá trị γ cho hầu hết các loại màn CRT nằm trong khoảng từ 2.2 tới 2.6, còn số lượng các hạt điện tử N tỉ lệ với điện áp V trên mỗi điểm ảnh. Vậy công thức I=k. 𝑁𝛾 có thể được viết dưới dạng
I=K. 𝑉𝛾 hay V=(𝐼/𝐾)1/𝛾
Giả sử ta có cường độ ánh sáng I thì bước đầu tiên ta phải làm là: Ta tìm giá trị Ij gần nhất qua phép làm tròn.Giá trị j tìm được là:
I= rj.I0 vậy rj = I/I0 => j=ROUND( log𝑟 (I/𝐼0))
Thay j vào công thức ta có: I= rj.I0
Bước tiếp theo của tiến trình là xây dựng mức điện áp Vj cho điểm ảnh mà cường độ ánh sáng có giá trị tương ứng là Ij
Vj=ROUND(Ij /K)1/𝛾
Nếu màn hình raster không có bảng mở rộng (look up table) thì giá trị Vj được đặt vào điểm hiển thị. Trong trường hợp ngược lại , giá trị của j sẽ được sử dụng là chỉ số để tìm ra giá trị của V tương ứng trong bảng.
6.1.2. Hiệu chỉnh Gama
Giá trị gama là số mũ của hàm lũy thừa, giá trị đó đối với loại phim nhựa 35mm thiết kế để xem trong phòng tối là 1.5
Hệ số gama của phim lại không giống với hệ số gama đối với loại màn hình CRT, loại thiết bị độ sáng phụ thuộc vào ống phóng tia điện tử.
Theo công thức V=(𝐼/𝐾)1/𝛾 độ sáng trên mặt màn hình CRT tỷ lệ với điện áp theo hàm mũ với giá trị mũ lên đến 5/2. Giá trị 2.5 mà thực tế giao động trong khoảng
2.3 đến 2.6 chính là đại lượng gama của loại màn hình CRT .
Hàm vẽ dưới đây cho thấy quan hệ không tuyến tính giữa giá trị của điện áp đầu vào với giá trị của cường độ sáng trên màn CRT và đó là một trong các đặc điểm cố hữu của màn hình loại này
Hình 6.1.CRT gamma
Sự phản hồi tuyến tính của CRT có thể được bù bởi phần cứng và phép bù này được gọi là phép hiệu chỉnh gama(gama correction) .
Việc sử dụng Ijlàm chỉ số trong look-up table để tìm ra cường độ sáng có các điểm ảnh trên màn hình gọi là phép hiệu chỉnh gama với bảng LUT.
Khi này giá trị của Ij được sử dụng chứ không phải Vj để đưa vào bộ đệm làm tươi hay bảng look-up table.
Vậy một câu hỏi đặt ra là bao nhiêu khoảng sẽ là đủ cho việc thể hiện một ảnh đen trắng liên tục?
Theo tính toán thì hệ số tỉ lệ r=1.01 là mức ngưỡng phân biệt của mắt . nếu r<1.01 thì mắt sẽ không phân biệt được sự khác lệch giữa hai cường độ sáng lân cận nhau Ij và Ij+1. Và như vậy số khoảng đủ n được tính ngược theo công thức
r=(1/I0)1/𝑛 => 1.01=(1/I0)1/𝑛
n=log1.01(1/I0)
Với 1/I0 là khoảng biến động của thiết bị phần cứng .
Khoảng biến động thông thường | Số lượng khoảng biến động n | |
CRT | 50-200 | 400-530 |
Máy in đồ họa | 100 | 465 |
Phim chiếu đồ họa | 100 | 700 |
Giấy phủ in đen trắng | 100 | 465 |
50 | 400 | |
In nhan đen trắng | 10 | 234 |
Hình 6.2. Bảng so sánh khoảng biến động của các thiết bị truy xuất đồ họa
6.1.3. Xấp xỉ bán tông
Phương pháp này dựa vào cấu tạo mắt của người cũng như nguyên lý thu nhận ảnh của mắt khi nhìn những vùng nhỏ ở khoảng cách xa.
Lúc đó mắt không phân biệt được các vật một cách cụ thể mà chỉ ghi nhận cường độ trung bình của vùng ảnh đó. Phương pháp này được gọi là xấp xỉ bán tông
Phương pháp này cho phép đạt độ phân giải trong in ảnh báo vào khoảng từ 60-
>80 dpi, còn trong tạp chí và sách cao hơn khoảng từ 110->120dpi
Với phương pháp xấp xỉ bán tông, mỗi một vùng đơn vị độ phân giải được hình dung như một ô vuông trắng, điền bởi các đường tròn đen trên theo mức độ phụ thuộc vào cường độ sáng trung bình của các điểm ảnh trong ảnh gốc. Nếu vùng ảnh càng thẫm màu thì số lượng và kích thước của đường tròn đen càng lớn. Như vậy kích thước của đường tròn đen sẽ tương đương với mức độ xám của vùng ảnh gốc tương ứng .
Các thiết bị in ấn và hiển thị cho phép điều khiển thay đổi được kích thước của điểm đen hay là bán kính của đường tròn đen thì việc mô tả mức độ xám của ảnh hoàn toàn có thể thông qua việc sắp xếp tương quan của các đường tròn với bán kính của chúng.
Trường hợp ngược lại thì việc mô phỏng kích thước của đường tròn đen trong đơn vị độ phân giải có thể thông qua một ma trận vuông các điểm ảnh. Tỉ lệ giữa các điểm ảnh đen và trắng trong ma trận tương tự như giữa đường tròn đen và vùng trắng .
Trong trường hợp này một số các kỹ thật sau thường được ứng dụng cho việc biến đổi ảnh trước khi đem ra sử lý
1. Phân ngưỡng
Phương pháp phân ngưỡng là lấy một giá trị bất kì hay trung bình của cả vùng ảnh làm ngưỡng và so với mức sáng của từng điểm ảnh trong ô.
Nếu giá trị của điểm lớn hơn giá trị của ngưỡng thì nó được bật (on). Nếu ngược lại thì tắt (off)
Giải thuật Halftone (x1, x2, y1, y2, T[n, m])
Giải thuật xấp xỉ bán tông giới hạn bởi x1, x2, y1, y2 Lx,Ly: Chiều dài các ô đơn vị theo x và y
T[i, j]: ngưỡng trong ô đơn vị xác định bởi i, j I(x,y): Cường độ sáng của điểm(x, y)
Begin
For y = y1 to y2 do For x = x1 to x2 do
i = x chia lấy phần nguyên là Lx; j = y chia lấy phần nguyên Ly;
if T[i, j] < I(x,y) then diem(x, y) ->on if T[i, j] >= I(x,y) then diem(x, y) ->off End
Nhược điểm: Phương pháp này chỉ đơn thuần là so sánh làm tròn giá trị cường độ của các điểm ảnh dựa trên một ngưỡng xác định => phương pháp này làm mất đi nhiều thông tin của ảnh nên gây ra một số các hiệu ứng phụ cho ảnh. Để giải quyết vấn đề trên người ta sử dụng kỹ thuật tạo mẫu tô
2. Mẫu tô
Biểu diễn một điểm ảnh trên màn hình theo các mẫu tô. Đơn vị nhỏ nhất của ảnh là lưới 2×2 chúng ta có 5 mức độ thể hiện cường độ sáng của vùng đơn vị .Ma trận kích thước n×n có 𝑛2+1 độ phân giải khác nhau
Hình 6.3. Các độ phân giải với ma trận 2×2 mẫu
Việc xác định kích thước của miền đơn vị phụ thuộc vào rất nhiều kích thước của thiết bị hiển thị, khoảng cách quan sát của người sử dụng cũng như ngưỡng chất lượng cần đạt được.
Việc đạt được các mức xám khác nhau dựa vào kích thước ma trận dành cho vùng điểm ảnh đơn vị .Tuy vậy chúng ta cần phải cân nhắc lựa chọn vị trí của các điểm ảnh vì nó quyết định tới chất lượng của ảnh khi hiển thị