với
η2
V3
1 η22 4D2η2
Khi cản nhỏ, hiện tượng cộng hưởng xẩy ra khi η ≈ 1
πn c
1
Ω ≈ ω0 → 30 ≈
πn 2
Có thể bạn quan tâm!
-
 Tính Toán Dao Động Tự Do Có Ma Sát Nhớt
Tính Toán Dao Động Tự Do Có Ma Sát Nhớt -
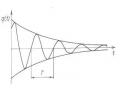
 A Đồ Thị Dao Động Tự Do Có Ma Sát Khô Với Điều Kiện Đầu 𝑡 = 0 ∶
A Đồ Thị Dao Động Tự Do Có Ma Sát Khô Với Điều Kiện Đầu 𝑡 = 0 ∶ -
 Đồ Thị Biểu Diễn Sự Phụ Thuộc Của Góc 𝛹 Vào 𝜂
Đồ Thị Biểu Diễn Sự Phụ Thuộc Của Góc 𝛹 Vào 𝜂 -
 Hình Bài Tập 2 Hình 2.46 Hình Bài Tập 3
Hình Bài Tập 2 Hình 2.46 Hình Bài Tập 3 -
 Phương Pháp Sử Dụng Phương Trình Lagrange Loại Ii.
Phương Pháp Sử Dụng Phương Trình Lagrange Loại Ii. -
 Đỗ Vòng Và Góc Xoay Của Đường Đàn Hồi Của Các Dầm Thẳng Có Tiết Diện Không Đổi.
Đỗ Vòng Và Góc Xoay Của Đường Đàn Hồi Của Các Dầm Thẳng Có Tiết Diện Không Đổi.
Xem toàn bộ 182 trang tài liệu này.
→ c ≈ M
Khi cộng hưởng
V3 2D
M 30
Để đơn giản ta bỏ qua lực cản. Khi đó phản lực pháp tuyến của nền tác dụng lên vỏ máy (hình 2.31c)
N = (M + m)g – cx
Do V3
≈ 1 nên ta có
2D
Nmin
= M + m g − cx
max
cx0
= M + m g −
2D
Điều kiện để vỏ máy không nhảy khỏi nền
cx0 cx0
N ≥ 0 → M + m g ≥ → D ≥
min
2D 2 M + m g
d. Tính toán dao động cưỡng bức bằng hàm đáp ứng tần số
Xét phương trình dao động của hệ tuyến tính một bậc tự do có cản và lực kích động điều hoà
my + by + cy = x t (3.33)
Trong đó kích động được biểu diễn dưới dạng hàm số phức
x t = X Ω eiΩt (3.34)
Ta sẽ tìm nghiệm của phương trình (3.33) dưới dạng
y t = Y Ω eiΩt (3.35)
Với Y(Ω) là hàm biên độ phức cần xác định. Đạo hàm bậc một và bậc hai của hàm y(t) theo thời gian t rồi thay vào phương trình (3.33) ta được
−mΩ2 Y Ω eiΩt + ibΩY Ω eiΩt + cY Ω eiΩt = X(Ω)eiΩt
Khử eiΩt ở hai vế phương trình trên và nhóm theo Y(Ω) ta được
c − mΩ2 + ibΩ Y Ω = X(Ω)
Từ đó suy ra
Y Ω
1X Ω
(3.36)
Nếu ta đặt
H Ω
c mΩ2 ibΩ
1
c mΩ2 ibΩ
(3.37)
thì biểu thức (3.36) có dạng
Y Ω = H Ω X Ω (3.38)
Định nghĩa: Hàm H(Ω) được xác định bởi công thức (3.37) được gọi là hàm đáp ứng tần số.
Nhân tử số và mẫu số của biểu thức (3.37) với c − mΩ2 − ibΩ ta được
c − mΩ2 − ibΩ
H Ω = c − mΩ2 + ibΩ c − mΩ2 − ibΩ = a + id
Với
c − mΩ2 bΩ
a = c − mΩ22 + b2 Ω2 ; d = − c − mΩ22 + b2Ω2
Từ đó suy ra môđun H(Ω) và argument φ của hàm đáp ứng tần số H(Ω)
a2 d 2
c mΩ22 b2Ω2
H(Ω) 1
(3.39)
φ arctg d arctg
bΩ
(3.40)
a c mΩ2
X(Ω)
c mΩ22 b2Ω2
Từ công thức (3.38) ta suy ra
Y(Ω)
H ΩX(Ω)
(3.41)
Biến đổi công thức (3.37) ta được
HΩ
1
c mΩ2 ibΩ
1 1
c 12 i2D
Hàm
ZΩ
1 iΩH(Ω)
được gọi là trở kháng cơ học.
e. Đệm đàn hồi của máy
Để giảm lực truyền xuống nền móng người ta dùng đệm đàn hồi. Giả sử máy có khối lượng m, đệm đàn hồi qui đổi thành lò xo có hệ số cứng c và giảm chấn có hệ số
b. Nếu trên máy chịu tác dụng một lực điều hoà F t = Fsin Ωt (hình 2.22a) thì lực truyền xuống nền được xác định bởi hệ thức
Ftđ = cx + bx (3.42)
Như đã biết, phương trình vi phân mô tả dao động của mô hình 2.22a có dạng
$
&x& 2δx& ω2x ω2F sin sin Ωt
0 0 c
(3.43)
Trong quá trình chuyển động bình ổn, nghiệm của phương trình trên có dạng
xFˆVη, Dsin Ωt Ψ
(3.33)
c 1
Thế biểu thức (3.44) vào phương trình (3.42) ta được
FFˆVη, Dcsin Ωt Ψ bΩ cos Ωt Ψ
tđ c 1
c2 b2Ω2
FˆVη, D
sin Ωt Ψ γ
(3.45)
c 1
Với
tgγ bΩ 2δΩ
0
c ω2
2
và do c2 + b2 Ω2 = c1 + bΩ2 = c 1 + 4D2η2
c
Ta có Ftđ = FV2 (η, D) sin Ωt − Ψ + γ (3.46)
Từ công thức (3.46) ta suy ra: Để cho lực truyền xuống nền móng nhỏ ta phải chọn các tham số của hệ sao cho hàm khuếch đại V2 đạt cực tiểu.
Nếu trên máy có bộ phận quay chưa được cân bằng sẽ sinh ra các lực ly tâm
(hình 2.22b). Nhờ có đệm đàn hội ta có thể giảm được lực truyền xuống móng máy. Như đã biết phương trình vi phân dao động của mô hình 2.22b có dạng
0
&x& 2δx& ω2x
m1r m0 m1
Ω2 sin Ωt
(3.47)
Nghiệm riêng của phương trình (3.47) có dạng
x m1r m0 m1
V3 η, Dsin Ωt Ψ
(3.48)
Thế (3.48) vào biểu thức (3.42) ta được
Ftđ
F
m1r
=
m0 + m1
m1r
=
V3η, D csin Ωt − Ψ + bΩ cos Ωt − Ψ
V η, D c2 + b2 Ω2 sin Ωt − Ψ + γ
tđ m0 + m1 3
c m1r m0 m1
η2V
η, Dsin Ωt Ψ γ
(3.49)
2
Nếu ta dựa vào hàm khuếch đại V4η, D = η2V2 (η, D) thì lực truyền xuống đất có dạng
F = cm1 rV η, D sin Ωt − Ψ + γ (3.50)
tđ m0+m1 4
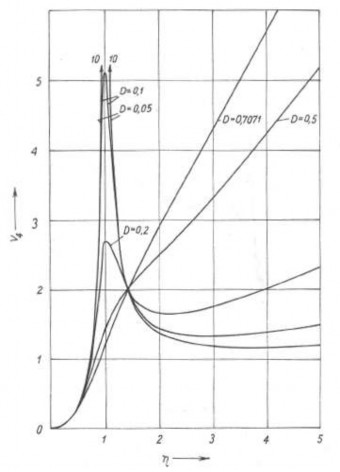
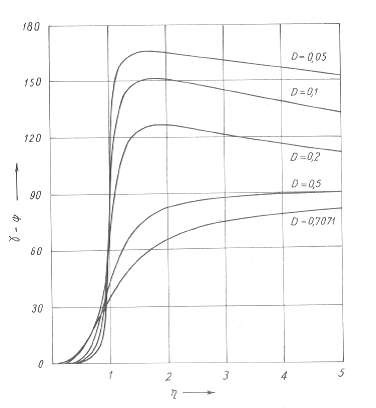
Sự phụ thuộc của hàm khuếch đại V4η, D và góc (γ − Ψ) vào η khi cho biết giá trị của D cho trên hình 2.32a và 2.32b.
Trong kỹ thuật ta cũng hay gặp bài toán do ảnh hưởng rung của nền các thiết bị trên nền móng làm việc sẽ kém chính xác. Trong trường hợp này ta sử dụng mô hình 2.22d. Nhờ có đệm đàn hồi sẽ làm giảm ảnh hưởng rung của nền móng lên các thiết bị đặt trên đó.
a)
b)
Hình 2.32a Đồ thị Sự phụ thuộc của hàm khuếch đại V4η, D và góc (γ − Ψ)
vào η
Thí dụ 2.16: Một máy gắn chặt vào móng và được đặt trên nền bằng một hệ lò xo song song. Khối lượng của máy và móng là 1000kg. Trong quá trình máy làm việc xuất hiện một lực điều hoà tác dụng theo phương thẳng đứng với biên độ 𝐹= 1000𝑁 và tần số f = 10Hz. Dưới ảnh hưởng của lực này móng dao động theo phương thẳng đứng. Hãy xác định hệ số cứng của lò xo sao cho chỉ có 5% lực tác dụng lên móng truyền xuống nền. Sau đó xác định độ lún tĩnh của móng và biên độ dao động của nó.
Lời giải: Mô hình cơ học của bài toán cho trên hình
2.33. Phương trình dao động của hệ là
mx + cx = Fsin Ωt
0
F
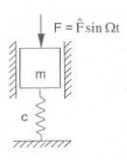
Hình 2.33 Hình thí dụ 2.16
Nghiệm dừng là
→ x + ω2 x =
sin Ωt
m
F1
x = sin Ωt c 1 − η2
Thế biểu thức nghiệm vào biểu thức tính lực truyền xuống nền ta được
Từ điều kiện
Ftđ
= cx = F1
1 − η2
sin Ωt
Ftđ1
F= 1 − η2= 0,05
ta suy ra η = 21 = 4,58
Hệ số cứng của lò xo tổng là
0
2
c = mω2 = m Ω
η2
2πf 2
= m η2
= 1000.
2π. 10 2 21
= 188N/mm
Với hệ số cứng đó, độ nén tĩnh của móng máy là
mg 1000.9,81
=
c 188
= 52,2 mm
Biên độ dao động dừng của móng máy là
1 F1000
x =1 − η2c = 20.188 = 0,266mm
e. Tính toán dao động cưỡng bức có ma sát khô
Phương trình vi phân mô tả dao động cưỡng bức của hệ có ma sát khô được viết dưới dạng
mq + cq + μmgsign q = Fcos Ωt + α (3.51)
Giả thiết ở các thời điểm t = 0, 2π
Ω
, 4π Ω
, … độ lệch q đạt cực đại (q = A, q = 0),
còn ở các thời điểm t = π , 3π , 5π
, … thì q = −A, q = 0. Như thế góc α là góc lệch
Ω Ω Ω
pha giữa lực cực đại và độ lệch cực đại.
Giả sử trong nửa chu kỳ đầu 0 ≤ t ≤ π Ω vận tốc q âm. Phương trình vi phân dao động trong nửa chu kỳ này là
mq + cq = μmg + Fcos Ωt + α (3.52) Nghiệm tổng quát của phương trình trên có dạng
q C1 cos ωo t C2 sin ω0t a
h 1 η2
cos Ωt α
(3.53)
Trong đó
0
ω2 = c
m
, a =
μmg c
F
, h =
c
Ω
, η =
ω0
Từ điều kiện q 0 = A, q 0 = 0 ta có
C1 a
h 1 η2
cos α A
(3.54)
C2ω0
Từ điều kiện
ta suy ra
hΩ 1 η2
sin α 0
π
q
Ω
π
= −A, q
Ω
= 0
(3.55)
C1 cos cos λ C2λ a
h 1 η2
cos α A
(3.56)
C1Ωsin λ C2Ω cos cos λ
hΩ 1 η2
sin α 0
(3.57)
trong đó
λ πω0
Ω
Như thế ta có hệ bốn phương trình (3.54) – (3.57) để xác định bốn ẩn C1 , C2 , A, 𝛼. Cộng các phương trình (3.54) và (3.56), (3.55) và (3.57) ta nhận được hệ hai phương trình để xác định C1 và C2
C11 + cos λ + C2 sin λ + 2a = 0
−C1 sin λ + C21 + cos λ = 0
Từ đó suy ra
λ C1 = −a ; C2 = −atg 2
Thế các kết quả này vào các phương trình (3.54) và (3.55) ta dẫn đến các phương trình
h
A = cos α 1 − η2
πω0 hη
−a tg
= sin α
2Ω 1 − η2
Từ đó suy ra công thức xác định biên độ
h a 1 η
2
2
1
πω 2
η 2Ω
tg0
1 η2
A (3.58)
Chú ý rằng khi Ω → 𝜔0(𝜂 → 1) ta có
lim 1 1 η2 tg π 4
η1 η 2η π
Do đó
h2
4a 2
π
1 η2
A (3.59)
Với sự phát triển của tin học, việc tính toán dao động cưỡng bức có ma sát khô sẽ trở nên đơn giản hơn nhiều, nếu ta sử dụng phương pháp số.
Ta xét phương trình dao động cưỡng bức có ma sát khô dạng
mq + cq = −μmgsign q + Fsin Ωt (3.60)
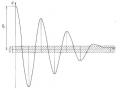
Với các số liệu m = 100kg, μ = 0,1 , ω0 = c m = 100s−1 , Ω = 200s−1 , F= 981N và các điều kiện đầu q 0 = q 0 = 0 ta dễ dàng tìm nghiệm của phương trình (3.60) bằng chương trình tính MATLAB. Kết quả lấy ra dưới dạng đồ thị như hình 2.34.
Nếu ta quan tâm đến ma sát nhớt thì phương trình vi phân dao động có dạng
0
&q& 2δq& ω2qμgsign q&
Fˆ sin Ωt m
(3.61)
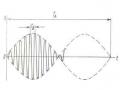
Với các số liệu như trên và cho thêm 𝛿 = 8, kết quả tính toán cho trên hình 2.35.
Một vài nhận xét về tính chất dao động cưỡng bức khi có ma sát
Qua các tính toán ở trên ta có thể rút ra một số nhận xét về tính chất của dao động tuyến tính có cản nhớt chịu kích động điều hoà ở trạng thái bình ổn như sau:
- Dao động cưỡng bức khi có cản xảy ra với tần số của lực kích động.
- Biên độ dao động cưỡng bức không phụ thuộc vào các điều kiện đầu và thời gian. Do đó khác với dao động tự do có cản, dao động cưỡng bức không tắt dần vì lực cản.
- Khi Ω = 𝜔0 biên độ dao động cưỡng bức tuy khá lớn, nhưng vẫn là đại lượng hữu hạn. Nó chưa phải là giá trị lớn nhất trong các giá trị của biên độ.
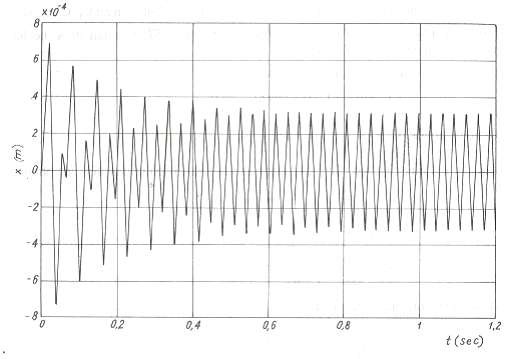
Hình 2.34 Dao động cưỡng bức tuyến tính có ma sát khô
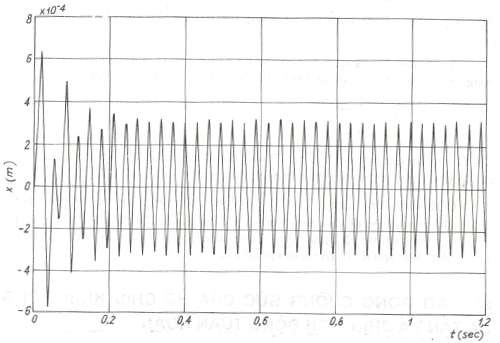
Hình 2.35 Dao động cưỡng bức tuyến tính có ma sát khô và nhớt