Hình Bài Tập 2 Hình 2.46 Hình Bài Tập 3

dạng

Khi hệ chịu tác dụng lực điều hoà F = Fsin Ωt, biên độ dao động cưỡng bức có

F

A = q =

0

ω2 − Ω22 + 4δ2Ω2

Từ điều kiện ∂A = 0 ta suy ra Ω2 = ω2 − 2δ2. Vậy A = A

khi Ω2 = ω2 −

∂Ω 0

max 0

2δ2. Biên độ dao động cưỡng bức đạt cực đại khi Ω nhỏ hơn 𝜔0 một chút.

- Trong dao động cưỡng bức có cản nhớt luôn xảy ra sự lệch pha giữa pha dao động và pha của lực kích động. Độ lệch pha đó được xác định bởi công thức

2δΩ

tgα =

0

ω2 − Ω2

Khi Ω = ω0 thì tgα = ∞ do đó α = π 2. Vậy dao động cưỡng bức khi cộng hưởng có pha lệch một góc π 2 so với pha của ngoại lực.

- Ở xa vùng cộng hưởng, biên độ dao động cưỡng bức với lực cản nhỏ không khác mấy so với biên độ dao động cưỡng bức không cản. Ở gần vùng cộng hưởng lực cản có một vai trò rất quan trọng. Trong vùng cộng hưởng độ lớn biên độ dao động cưỡng bức phụ thuộc rò rệt vào hệ số cản.

2.2.2.2 Một số thí dụ giải mẫu

Thí dụ 2.17:

Vật có khối lượng m = 5kg đặt trên nền nhẵn. Các lò xo có độ cứng c1 = c3 = 104 N/m, c2 = c4 = c5 = 103 N/m.

Hãy xác định độ cứng tương đương của hệ lò xo và tần số dao động riêng của hệ (Hình 2.36)

C1

C

C 4 C5

2

m

C3

Hình 2.36 Hình thí dụ 2.17

Lời giải

Độ cứng tương đương của các lò xo song song c1, c2, c3: c13 = c1 + c2 + c3

Độ cứng tương đương của các lò xo nối tiếp c4, c5:

45

1  1  1 c c4c5

c

c45 c4 c5

4 c5

Độ cứng tương đương của các lò xo song song c13 và c45:

c* c13

c45

c1

c2

c3 

c4c5

c c

 21,5.103 N / m

4 5

c *

m

Tần số dao động riêng của hệ:

0 

 65,574

rad / s

Thí dụ 2.18:

Trọng lượng vật treo là P. Lò xo có độ dài tự nhiên l, độ cứng c, trọng lượng P0.

Tìm chu kỳ dao động của vật (Hình 2.37)

Lời giải

Biến dạng của lò xo tại vị trí s:

x(s) x x(s) x. s s l l

2

s22s

l

s

x

Hình 2.37 Hình thí dụ 2.18

Suy ra:

x(s)

x. ;

l

x (s)

x . ;

l2

Động năng của lò xo:

1 1 P

Tlx 

v2 (s)dm;

2

0

dm 0 d gl

Động năng của hệ:

2 1 2

P P0

T P x2P0x s ds 

3 x2

0

2g 2gL l2 2g

Thế năng của lò xo đối với vị trí cân bằng tĩnh của vật:

c x2

2

Thay vào phương trình Lagrange loại II:

d (T ) T 

dt xx x

Phương trình vi phân dao động của hệ:

P P0

3 xcx  0

g

3

cg

P P0

Chu kỳ:  2

Nhận xét: Khi kể đến trọng lượng P0 của lò xo, trọng lượng cả hệ coi như tăng lên P0/3.

Thí dụ 2.19

Vôlăng được gắn vào thanh bằng thép dài l = 2m, đường kính d = 0,5 cm. Cho vôlăng một góc quay ban đầu rồi thả ra, người ta đo được 10 dao động xoắn trong 30,2s.

l

Tìm mômen quán tính đối với trục quay của vôlăng và thanh. Biết môđun trượt của thép G = 80.109 N/m2. (Hình 2.38)

Lời giải

Phương trình vi phân chuyển động của hệ:

Jc

 0;

c



J



Tần số riêng của dao động xoắn:

 210 2,081

0 30,2

rad / s

Hình 2.38

Độ cứng của thanh: c = GIp/l

Với Ip là mômen quán tính độc cực của mặt cắt ngang

Hình thí dụ 2.19

I p 

d 4

32

(0,5.102 )4

32

 0,006136.108

Độ cứng:

80.109  0,006136.108

c 

2

 2,455

Nm / rad

Suy ra:

Thí dụ 2.20

J c



2

0

 2,455

2,0812

 0,567

kgm2

Đĩa tròn đồng chất bán kính r, khối lượng m, lăn không trượt trên nền ngang.

Hai lò xo cùng có độ cứng c, nối với đĩa ở khoảng cách OA = a tới tâm đĩa.

Tìm tần số dao động riêng của đĩa (Hình 2.39)

Lời giải

X

c

c

A

a

O

Động năng của đĩa:

T 1mx21J 2

2 2 0

1 1 x2 3

Tmx2mr2

mx2

2 2 r  4

Thế năng của hai lò xo

1 a r 2

Hình 2.39 Hình thí dụ 2.20

 2 c

2 r

x2



Phương trình vi phân chuyển động của đĩa:

4c(a r)2

x x  0

3mr2

4c(a r)2

3mr2

Tần số riêng của dao động:

Thí dụ 2.21

0 

rad / s

Một vật thể dao động tịnh tiến, lực cản tỷ lệ bậc nhất với vận tốc (Hình 2.40). Trong 3 giây người ta đo được đúng 11 độ lệch cực đại theo hai phía (tức là 5 dao động) và ghi lại kết quả dưới dạng bảng số như sau:

0	1	2	3	4	5	6	7	8	9	10
ymax (mm)	12,0	-10	7,6	-6,2	5,3	-4,2	3,5	-2,7	2,1	-1,8	1,4

Có thể bạn quan tâm!

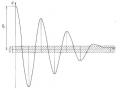
• A Đồ Thị Dao Động Tự Do Có Ma Sát Khô Với Điều Kiện Đầu 𝑡 = 0 ∶
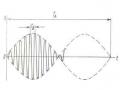
• Đồ Thị Biểu Diễn Sự Phụ Thuộc Của Góc 𝛹 Vào 𝜂
• Dao động kỹ thuật - 9
• Phương Pháp Sử Dụng Phương Trình Lagrange Loại Ii.
• Đỗ Vòng Và Góc Xoay Của Đường Đàn Hồi Của Các Dầm Thẳng Có Tiết Diện Không Đổi.
• Phương Pháp Giải Trực Tiếp (Ma Trận Cản Tùy Ý)

Xem toàn bộ 182 trang tài liệu này.

Hãy xác định độ tắt lôga  và hệ số cản  của dao động

m

y

b

c

Lời giải

Chu kỳ dao động tắt dần: Độ tắt lôga:

T* 1 ln 1,4  0,424

T* 3  0,6s 5

5 12

Hệ số cản:



T *

0,424  0,707

0,6

s1

Hình 2.40 Hình thí dụ 2.21

Thí dụ 2.22

Trong bài toán thiết kế, người ta phải lắp các phần tử cản và phần tử đàn hồi nối tiếp nhau như hình 2.41.

Hãy thiết lập phương trình vi phân dao động của hệ và tìm điều kiện xuất hiện dao động tự do có cản.

x2

x1

Lời giải

Gọi A là điểm nối giữa lò xo và phần

A

B

b

c

m

tử cản.

Điểm A chịu tác dụng của lực

Fcb.x1.

Biến dạng của lò xo là: x2 – x1

Tại điểm B xuất hiện lực đàn hồi Fdh

Hình 2.41 Hình thí dụ 2.22

= c(x2 – x1)

Tách riêng phần tử lò xo AB ta có:

Fc bxFdh c(x2 x1)

Áp dụng định luật Newton hai đối với chất điểm m ta có

(1)

mx2c(x2x1)

Từ (1) và (2) ta có:

(2)

bxc(x x ) mxxmx

(3)

1 2 1

2 1 b2

Từ (3) suy ra:

x m xE

(4)

1 b 2

Trong đó E là hằng số tích phân. Thay (4) vào (2) ta được:

mxc(x m xE) mxcm xcx

cE

(5)

2 2 b 2 2 b 2 2

Hằng số E được xác định từ các điều kiện đầu. Nếu cho x1(0) = 0, E=0 khi đó phương trình (5) có dạng:

x2(0)  0

thì

xc xc x  0

(6)

2 b 2 m2

0

Từ đó suy ra: 2 c ;

m

c

2b

c

m

1 mc

Điều kiện < 0 dẫn đến: c b

2b 2

Thí dụ 2.23

Vật có khối lượng m = 0,5kg, lò xo có độ cứng c = 245 N/m, hệ số ma sát trượt giữa vật và nền là  = 0,2. Kéo vật sao cho lò xo dãn 3 cm rồi buông ra không vận tốc ban đầu (Hình 2.42). Hãy tìm:

- Chu kỳ dao động và biên độ dao động tắt dần.

- Vật thực hiện được bao nhiêu dao động cho tới lúc dừng.

Lời giải

Lực ma sát phụ thuộc vận tốc của vật: N



mg Fms mg

khi khi

x 0

c

Fms

x

x 0

Phương trình vi phân chuyển động của vật:

mxcx mg mxcx mg

(x 0)

(x 0)

Đặt: 2 c ; s mg 0,2.0,5.9,81  0,004m

Hình 2.42 Hình thí dụ 2.23

0 m c

245

dạng:

Hai phương trình vi phân trên được viết dưới

0

xs2x s 0

Do đó chu kỳ của dao động tắt dần:

(1)

T* 2



 2

 2

 0,284s

m

c

0,5

245

Thời gian chuyển động giữa hai không điểm: T *  0,142s

2

Nghiệm của phương trình (1) được tìm dưới dạng: (x  s) = Asin0t + Bcos0t.

Từ điều kiện đầu ta có:

t = 0; x0 = 3 cm,

x0 0

 A = 0; x0  s = B

Do vật chuyển động theo hướng âm, nên: B = x0 – s x – s = (x0 – s)cos0t

Biên độ đầu tiên được xác định từ điều kiện x 0



d (x s) (x s) sin t  0 t 

dt 0 0 0 

Do đó: x1 = -(x0 – 2s) = -2,2 cm (tính từ 0)

Đối với dao động tiếp theo, các điều kiện đầu mới là:

t 

0

; xt

(x0

 2s)

x  s = Csin0t + Dcos0t C = 0; D = x0 – 3s

x2 = x0 – 4s = 1,4 cm Tương tự, ta có (Hình 1.8)

x3 = -(x0 – 6s) = -0,6 cm x4 = (x0 – 8s) = -0,2 cm

Vậy vật đã thực hiện 4 dao động với khoảng cách giữa 2 đỉnh lần lượt là: x0 + |x1| = 3 + 2,2 = 5,2 cm; |x1| + x2 = 2,2 + 1,4 = 3,6 cm

x2 + |x3| = 1,4 + 0,6 = 2,0 cm; |x3| + x4 = 0,6 – 0,2 = 0,4 cm.

c

Thí dụ 2.24

Pitton có khối lượng m = 0,01kg; diện tích S = 4 cm2;

chịu áp suất hơi theo luật:

p  40  30sin 2t



(N / cm2 ) .

hơi

Trong đó: T - Thời gian quay 1 vòng của trục máy tạo

m

Lò xo có độ cứng c =30 N/cm (Hình 2.43) Xác định dao động của pitton khi trụ máy tạo hơi quay 3

vòng/s. Hình 2.43

Hình thí dụ 2.24

Lời giải

Gọi  = 3 vòng/s = 6 rad/s Lực kích động:

P  p.S S(40  30sin 2t); T 21 s

 3

Phương trình vi phân dao động của pitton:

mxcs S (40  30 sin t)

x2x 40S 30S sin t

0 m m

Tìm nghiệm riêng dưới dạng

x Asin t B x2Asin t

Sau khi thay vào phương trình vi phân, so sánh các hệ số ta được:

A  30S

c m2

 30  4

30  0,01 362

 4,5 cm

B  40S  40  4  16 cm

c 30 3

Dao động của pitton: Biên độ A = 4,5 cm.

x  4,5sin 6t 16

3

CÂU HỎI ÔN TẬP

c1

c2

c2

1. Hãy xác định độ cứng tương đương và tần số dao động riêng của hệ lò xo trên các hình sau:

c1

c2

m

c 3

c 4

c1

c2 c3

m

c 4

c3

m

c

EJ

m

EJ

c

m

EJ

c

m

EJ

c

m

Hình 2.44 Hình bài tập 1

2. Một trục quay dài l, nằm ngang, mang hai đĩa ở hai đầu. Mô men quán tính của các đĩa đối với trục quay là J1 và J2. Độ cứng xoắn của trục là c. Hãy xác định quy luật dao động tương đối của hai đĩa (hình 2.45).

3. Đĩa tròn đồng chất có khối lượng m = 50kg, bán kính r = 0,5m lăn không trượt trên nền ngang Lò xo có độ cứng c = 75 N/m, hệ số cản nhớt b = 10 Ns/m (hình 2.46). Xác định:

- Độ cản δ và độ cản Lehr D, tần số , chu kỳ dao động tắt dần

- Chuyển động x(t) của tâm đĩa, khi t = 0, x = -0,2 m, 𝑥 = 0.

c

r



X

1

b

J2

J1

Hình 2.45 Hình bài tập 2 Hình 2.46 Hình bài tập 3