Lời giải: Áp dụng định lý biến thiên mômen động lượng đối với trục ds đi qua A và do 𝜑 nhỏ lấy xấp xỉ 𝑠𝑖𝑛𝜑 ≈ 𝜑 , 𝑐𝑜𝑠𝜑 ≈ 1, ta nhận được phương trình vi phân dao động của hệ
φ +
b c
φ + +
4m m
g
φ = 0
2a
0
→ φ + 2δφ + ω2φ = 0
Có thể bạn quan tâm!
-
Các Thí Dụ Về Thiết Lập Phương Trình Vi Phân Dao Động -
Xác Định Các Tham Số Độ Cứng Của Hệ Dao Động -
Tính Toán Dao Động Tự Do Có Ma Sát Nhớt -
Đồ Thị Biểu Diễn Sự Phụ Thuộc Của Góc 𝛹 Vào 𝜂 -
Dao động kỹ thuật - 9 -
Hình Bài Tập 2 Hình 2.46 Hình Bài Tập 3
Xem toàn bộ 182 trang tài liệu này.
Trong đó
b c g
2δ = , ω2 = +
4m 0
m 2a
Để hệ có khả năng dao động nhỏ thì δ < ω0. Từ đó suy ra
b c g
< +
8m m 2a
→ b < 8
cm +
gm2 2a
Từ các công thức (2.10) và (2.15) ta có
2𝜋𝐷
10 = 𝑙𝑛
1 − 𝐷2 𝑞
𝑞𝑛
= 𝑙𝑛10 → 𝐷 =
1
10
20𝜋2
0,037
Chu kỳ dao động
𝑛 +10
𝑙𝑛 + 1
2π 2π 2π T = =≈
ω ω01 − D2 ω0
= 2π
2am 2ac + gm
2.2.2 Tính toán dao động tự do có ma sát khô
Xét dao động của hệ mô tả trên hình 2.20. Lực ma sát khô (hay ma sát Coulomb) có hướng phụ thuộc vào vận tốc của vật thể m
Fms
= −μmg khi q > 0 μmg khi q < 0
c
m
q
.
Fms q.<0
q>0
Hình 2.20 Hệ dao động tự do có ma sát khô
Phương trình vi phân dao động của hệ có dạng
mq + cq − μmg = 0 khi q < 0 (2.16)
mq + cq + μmg = 0 khi q > 0 (2.17)
Nếu ta đưa vào các ký hiệu
c = ω2 , μmg = s
m 0 c
thì các phương trình (2.16) và (2.17) có dạng
0
(q − s).. + ω2(q − s) = 0 khi q < 0 (2.18)
0
(q + s).. + ω2(q + s) = 0 khi q > 0 (2.19)
Dễ dàng tính được nghiệm tổng quát của các phương trình trên
q = A1 cos ω0 t + α1+ s khi q < 0 (2.20)
q = A2 cos ω0t + α2− s khi q > 0 (2.21)
m
c
Chu kỳ dao động của hệ là
T 2π 2π ω
(2.22)
Để xác định biểu thức nghiệm, cần phải biết các điều kiện đầu. Giả sử tại thời điểm đầu t = 0 ∶ q 0 = q0, q 0 = 0 . Trong nửa chu kỳ đầu q < 0 ta có
q t = A1 cos ω0t + α1+ s
Các hằng số A1 và 𝛼1 được xác định từ các điều kiện đầu. Ta có các phương
trình
q 0 = A1 cos α1 + s = q0 q 0 = −ω0A1 sin α1 = 0
Giải hai phương trình trên ta được α1 = 0, A1 = q0 − s. Như thế trong nửa chu
kỳ đầu 0 ≤ t ≤ πvật điểm dao động theo qui luật
ω0
q t = q0 − s cos ω0t + s (2.23)
Từ biểu thức (2.23) ta xác định được điều kiện đầu cho dao động ở nửa sau của
chu kỳ đầu
t T π
0 2 ω0
2
qTq
2
q&T 0
0 scoscos π s 2s q0
trình
Trong nửa sau của chu kỳ đầu q > 0 ta có
q t = A2 cos ω0 t + α2− s
Các hằng số A2 và 𝛼2 được xác định từ các điều kiện đầu. Ta có các phương
q T q π A cos cos π α s 2s q
2 ω 2 2 0
0
&T
π
q 2 q&ωω0A2sin sin π α2 0
0
Từ hai phương trình trên suy ra α2 = 0, A2 = q0 − 3s. Như thế trong nửa thứ
π 2π
hai của chu kỳ đầu t
vật điểm dao động theo qui luật
ω ω
0 0
q t = q0 − 3s cos ω0t − s (2.24)
Từ biểu thức (2.24) ta xác định được các điều kiện đầu cho dao động ở nửa đầu chu kỳ thứ hai
q T = q0 − 4s , q T = 0
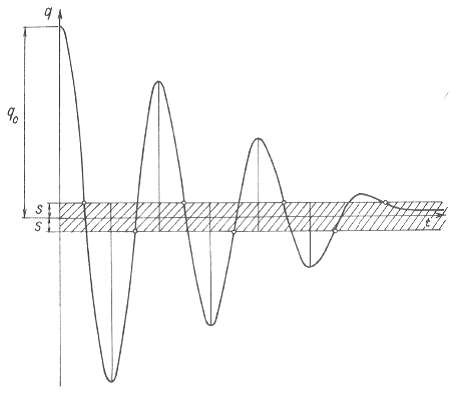
Sau đó tiếp tục tính toán tương tự như trên. Đồ thị dao động tự do có ma sát khô tương ứng với điều kiện đầu t = 0 ∶ q 0 = q0 , q 0 = 0 có dạng như hình 2.21a.
Hình 2.21a Đồ thị dao động tự do có ma sát khô với điều kiện đầu 𝑡 = 0 ∶
𝑞 0 = 𝑞0 , 𝑞 0 = 0
Ngày nay việc tính toán dao động có thể thực hiện khá đơn giản trên máy tính điện tử. Hai phương trình (2.16) và (2.17) có thể viết lại dưới dạng
0
x + ω2 x = −μgsign x (2.25)
Trong đó
1khi x& 0
sign x&1khi x& 0
(2.26)
Cho biết ω0 = c m = 100s−1 , μ = 0,1 , g = 9,81m/s2 . Với các điều kiện đầu 𝑥 0 = 0,005𝑚 , 𝑥 0 = 0 , sử dụng chương trình MATLAB, ta dễ dàng tính được nghiệm của phương trình (2.25). Đồ thị biểu diễn kết quả tính toán có dạng như hình 2.21b.
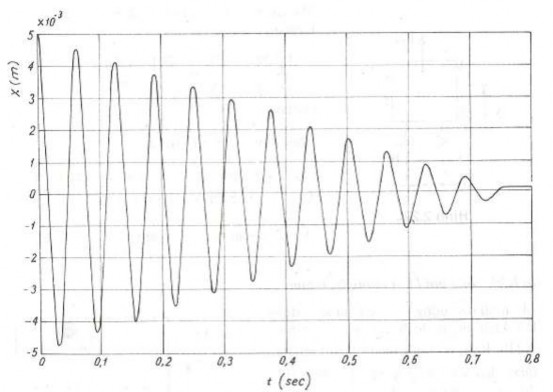
Hình 2.21b Dao động tự do có tính đến ma sát khô
2.2.2.1 Dao động cưỡng bức của hệ chịu kích động điều hoà
a. Các dạng kích động và phương trình vi phân dao động
* Kích động lực
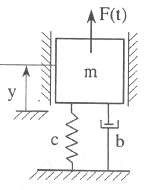
Trên hình 2.22a là mô hình dao động khối lượng – lò xo chịu kích động lực. Giả sử F t = FsinΩt, trong đó Flà giá trị cực đại của hàm F(t). Đối với mô hình này ta có
T = 1
2
my2
, Π =
1 cy2
2
, Φ =
1 by2
2
, Q∗
= F(t)
Thế các biểu thức trên vào phương trình Lagrange loại 2
d ∂T ∂T
−
∂Π ∂Φ
= − −
+ Q∗
dt ∂y ∂y
ta được
∂y ∂y
my + by + cy = FsinΩt (3.1)
Chia hai vế của (3.1) cho m và đưa vào ký hiệu
y = F c , ta biến đổi (3.1) về dạng Hình 2.22 Hệ chịu kích động lực
0 0
&y& 2δy& ω2y ω2yˆsinΩt
* Kích động bởi khối lượng lệch tâm
(3.1a)
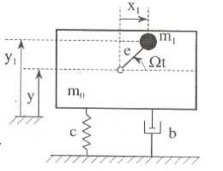
Mô hình dao động của hệ chịu kích động bởi khối lượng lệch tâm cho trên hình 2.22b. Rôto có khối lượng lệch tâm m1 , quay đều với vận tốc góc Ω. Biểu thức động năng của hệ có dạng
T = 1 2 1 2
m0y
2
Do
+ m1v1 2
x1 = ecosΩt , x 1 = −eΩsinΩt ,
y1 = y + esinΩt , y 1 = y + eΩcosΩt
nên ta có
v2 = x 2 + y 2 = y 2 + 2y eΩcosΩt + e2Ω2
1 1 1
Từ đó suy ra
T 1 my&2 m y&eΩcosΩt 1 m e2Ω2
Hình 2.22b Hệ chịu kích động bởi khối lượng lệch tâm
2 1 21
Trong đó m = m0 + m1
Các biểu thức thế năng Π và hàm hao tán Φ có dạng như các thí dụ trước
1 1
Π = cy2 , Φ = by2
2 2
Thế các biểu thức T, Π, Φ vào phương trình Lagrange loại 2, ta được
my + by + cy = m1eΩ2sinΩt (3.2)
Biến đổi tương tự như trên ta được
0
y + 2δy + ω2y = Ω2 y sinΩt (3.2a)
trong đó
yˆ
m1 e m0 m1
* Kích động bằng lực đàn hồi
Trên hình 2.22c là mô hình hệ chịu kích động lực đàn hồi tuyến tính. Bỏ qua ma sát trượt động μ = 0 . Cho biết u t = u sinΩt
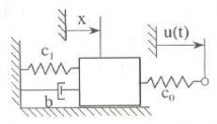
Phương trình vi phân dao động của hệ có
dạng
mx + bx + c1x + c0x − u(t) = 0
Do u t = u sinΩt nên ta có
mx + bx + cx = c0u sinΩt (3.3)
trong đó c = c1 + c0.
Nếu sử dụng ký hiệu
xˆ=
c0uˆ
c1 +c0
thì phương
Hình 2.22c Hệ chịu kích động bằng lực đàn hồi
trình (3.3) biến đổi được về dạng
x + 2δx + ω2x = ω2 x sinΩt (3.3a)
0 0
* Kích động động học
m
y
b
c
u(t)
Trên hình 2.22d là mô hình hệ chịu kích động động học. Giả sử điểm chân của bộ lò xo và cản nhớt chuyển động theo qui luật điều hoà u t = u sinΩt. Phương trình vi phân dao động của hệ có dạng
mx + b y − u + c y − u = 0
Thế u t = u sinΩt , u t = u ΩcosΩt vào phương trình trên ta được
my + by + cy = u csinΩt + bΩcosΩt (3.4)
Chia hai vế của phương trình (3.4) cho m ta
được
0
y + 2δy + ω2y =
Ω
ω
= ω0y ω0sinΩt + 2δ
0
trong đó y = u .
cosΩt (3.4a)
Hình 2.22d Hệ chịu kích động
động học
* Kích động bằng lực cản nhớt
Trên hình 2.22e là mô hình hệ chịu kích
động bằng lực cản nhớt. Mặt trượt nhẵn tuyệt đối μ = 0 . Phương trình vi phân dao động của hệ có dạng
x
b1
u(t)
c
b0
mx + b1x + cx + b0x − u (t) = 0
Cho biết u t = u sinΩt , u t = u ΩcosΩt , khi đó phương trình trên có dạng
mx + bx + cx = b0u ΩcosΩt (3.5)
với b = b1 + b0.
Chia hai vế của (3.5) cho m, ta được
0
x + 2δx + ω2x = 2δΩx cosΩt (3.5a)
trong đó x = b0u .
b
Qua các thí dụ trên ta thấy: Phương trình vi phân dao động tuyến tính của hệ một bậc tự do chịu kích động điều hoà có dạng
Hình 2.22d Hệ chịu kích động động học
hoặc
mq + bq + cq = H1sinΩt + H2cosΩt (3.6)
0
q + 2δq + ω2q = h1sinΩt + h2cosΩt (3.7)
Chú ý, nếu ta sử dụng độ cản Lehr D thì phương trình (3.1a) có dạng như sau
y + 2Dω0y + ω2y = ω2y sinΩt (3.8)
0 0
trong đó
0
ω2 c, D δ b
cm
m ω02
ứng.
dạng
Ta có thể biến đổi các phương trình (3.2a), (3.3a), (3.4a), (3.5a) về dạng tương
b. Tính toán dao động cưỡng bức không cản
Phương trình vi phân dao động cưỡng bức không cản của hệ một bậc tự do có
mq + cq = HsinΩt (3.9)
Nếu ta đưa vào các ký hiệu
0
ω2
c , h H m m
thì phương trình (3.9) có dạng
0
q + ω2 q = hsinΩt (3.10)
Nghiệm tổng quát của phương trình vi phân (3.10) bao gồm nghiệm tổng quát của phương trình vi phân tuyến tính thuần nhất tương ứng và một nghiệm riêng của phương trình có vế phải. Để giải phương trình vi phân (3.10) ta xét hai trường hợp Ω ≠ 𝜔0(xa cộng hưởng) và Ω ≈ 𝜔0 (gần cộng hưởng).
Khi Ω ≠ 𝜔0 ta tìm nghiệm riêng của phương trình (3.10) dưới dạng
q∗ = AsinΩt (3.11)
Trong đó A là hằng số chưa xác định. Thế biểu thức (3.11) vào phương trình (3.10), so sánh với các hệ số của sinΩt, ta rút ra biểu thức xác định A
A h
0
ω2 Ω2
với (Ω ω0 )
Theo lý thuyết phương trình vi phân, nghiệm tổng quát của phương trình (3.10) có dạng
q t C cos ω t C sin ω t h sinΩt
(3.12)
0
1 0 2 0
ω2 Ω2
Các hằng số C1, C2 được xác định từ các điều kiện đầu. Giả sử khi t = 0 thì q(0)
= qo ; q 0 = q 0. Thế các điều kiện đầu này vào biểu thức (3.12) và đạo hàm của nó, ta có
C q ;C
q&0 hΩ
1 0 2 ω ω ω Ω
0 0
Như thế, biểu thức nghiệm (3.12) có dạng
q t q cos ω t q&0sin ω t hΩ sin ω t h sinΩt
0 0
0
0
(3.13)
ω
ω ω2 Ω2
ω2 Ω2
0 0 0 0
Nghiệm (3.13) gồm hai phần: Ba số hạng đầu biểu thị dao động tự do với tần số là tần số riêng của hệ, số hạng thứ tư biểu thị dao động cưỡng bức với tần số là tần số của lực kích động. Chú ý rằng khi q0 = q 0 = 0 chỉ có hai số hạng đầu của dao động tự do triệt tiêu. Vì vậy số hạng thứ ba được gọi là thành phần dao động với tần số lực kích động và các thành phần dao động với tần số riêng được gọi là giai đoạn chuyển tiếp. Giai đoạn chỉ tồn tại thành phần dao động với tần số của lực kích động được gọi là giai đoạn bình ổn.
Nếu bỏ qua các thành phần dao động tự do trong (3.13) ta có biểu thức xác định trạng thái bình ổn của dao động cưỡng bức
0
q* t
h ω2 Ω2
sinΩt
H
c(1 η2 )
sinΩt
(3.14)
Chú ý rằng thừa số H/c là dịch chuyển gây ra bởi lực tĩnh H đặt vào vật rắn dao động. Trong đó 𝜂 = Ω 𝜔0. Đại lượng
V η 1
1 η2
(3.15)
biểu thị tác dụng động lực của lực kích động, và được gọi là hàm khuếch dại (hoặc hệ số động lực). Trên hình 2.23 biểu diễn sự phụ thuộc của V vào η.
V
1
O 1
Hình 2.23 Đồ thị biểu diễn sự phụ thuộc V vào
Khi tỷ số Ω 𝜔0 dần đến 1 thì hàm khuếch đại (hệ số động lực) và do đó biên độ dao động cưỡng bức tăng lên nhanh chóng và tiến tới vô cùng khi Ω = ω0 . Hiện tượng đó gọi là hiện tượng cộng hưởng. Như vậy hiện tượng cộng hưởng là hiện tượng biên độ dao động cưỡng bức tăng lên rất lớn do tần số của lực kích động trùng với tần số dao động tự do. Trong thực tế không có trường hợp nào biên độ dao động tăng lên vô cùng vì trong các hệ thực bao giờ cũng tồn tại lực cản. Vấn đề này sẽ được xét ở sau.
Trở lại biểu thức tổng quát (3.13) của nghiệm. Khi q0= q 0 = 0, biểu thức nghiệm (3.13) có dạng
q t hsinΩt Ω sin ω t
(3.16)
ω2 Ω2 ω 0
0 0