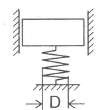
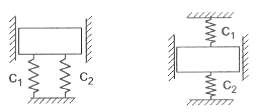
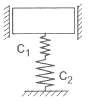
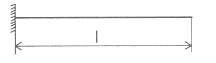
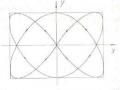
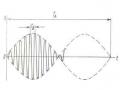
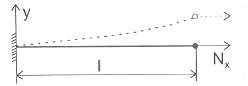
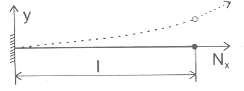
Hệ trên hình 2.13d là một hệ siêu tĩnh đơn giản. Nếu ta giải phóng liên kết tại A và thay bằng ngẫu lực có mômen chưa biết M thì độ vòng và góc xoay ở đầu A có thể xác định theo các công thức:
Fh3
w =
3EI
Mh2
−
2EI
, φ =
Fh2 Mh
−
2EI EI
Từ điều kiện bổ sung góc xoay ở A bằng không ta suy ra
𝑀 =
𝐹 2
→ 𝑤 =
𝐹3 12𝐸𝐼
→ 𝑐∗ = 2𝑐 =
2𝐹
𝑤
24𝐸𝐼
= 3
Tần số riêng của hệ
c∗ 24EI
−1 ω0
ω0 =m =h3m → ω0 = 8,1s
→ f = = 1,3Hz 2π
Sơ đồ | Hệ số c | |
1 |
| Gd4 8nD3 d – Đường kính thiết diện D – Đường kính lò xo G – Mô đun trượt; n – Số vòng lò xo |
2 |
| c1 + c2 |
3 |
| c1c2 c1 + c2 |
4 |
| 3EI l3 |
5 |
| 3EI(a + b) a2b2 |
6 |
| 12EI a + b 3 a3b23a + 4b |
Có thể bạn quan tâm!
-
Biểu Diễn Dao Động Tuần Hoàn Trên Mặt Phẳng Pha -
Các Thí Dụ Về Thiết Lập Phương Trình Vi Phân Dao Động -
Xác Định Các Tham Số Độ Cứng Của Hệ Dao Động -
A Đồ Thị Dao Động Tự Do Có Ma Sát Khô Với Điều Kiện Đầu 𝑡 = 0 ∶ -
Đồ Thị Biểu Diễn Sự Phụ Thuộc Của Góc 𝛹 Vào 𝜂 -
Dao động kỹ thuật - 9
Xem toàn bộ 182 trang tài liệu này.
Số TT
| 3EI(a + b)3 a3b3 | |
8 |
| 3EI b + l b2 |
9 |
| 12EI 4b + 3l b2 |
10 |
| α2EI Nx α = αl chαl − shαl EI |
11 |
| α2EI shαl Nx α = l αl chαl − shαl EI |
7
2.2 DAO ĐỘNG TỰ DO CÓ CẢN
Quan sát các hệ dao động, ta thấy dao động tự do nói chung tắt dần theo thời gian. Tính chất này của hệ dao động lý giải bởi ảnh hưởng của lực cản. Hai loại lực cản phổ biến nhất là lực ma sát nhớt tỷ lệ bậc nhất với vận tốc và lực ma sát khô.
2.2.1 Tính toán dao động tự do có ma sát nhớt
Xét dao động của hệ mô tả trên hình 2.14. Do có thêm lực cản nhớt tỷ lệ bậc nhất với vận tốc, nên phương trình vi phân dao động của hệ
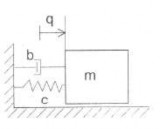
có dạng
mq + bq + cq = 0 (2.1)
Nếu ta đưa vào các ký hiệu
c = ω2 , b = 2δ (2.2)
m 0 m
thì phương trình (2.1) có dạng
0
q + 2δq + ω2q = 0 (2.3)
Theo lý thuyết phương trình vi phân tuyến tính [1], phương trình đặc trưng của (2.3) là
Hình 2.14 Hệ dao động có cản nhớt
0
λ2 + 2δλ + ω2 = 0 (2.4)
Tuỳ theo quan hệ giữa δ và ω0, có thể xảy ra các trường hợp sau
0
0
δ < ω0 (lực cản nhỏ): λ1,2 = −δ ± i ω2 − δ2 δ ≥ ω0 (lực cản lớn): λ1,2 = −δ ± δ2 − ω2
a. Trường hợp thứ nhất: 𝜹 < 𝝎𝟎 (lực cản nhỏ)
Trong trường hợp này 𝜆 có giá trị phức. Nghiệm tổng quát của phương trình vi phân dao động (2.3) có dạng
q = e−δtC1cosωt + C2sinωt (2.5)
trong đó
ω = ω2 − δ2 (2.6)
0
Các hằng số C1 , C2 được xác định từ các điều kiện đầu
t = 0 ∶ q 0 = q0 , q 0 = q 0
Từ các điều kiện đầu đã cho, dễ dàng xác định các hằng số C1 , C2
q 0 + δq0
C1 = q0 , C2 =
(2.7)
ω
Để biến đổi biểu thức (2.5) ta đưa vào các hằng số A và β xác định theo hệ thức
C1 = Asinβ , C2 = Acosβ
Từ đó suy ra
A = C2 + C2 , tgβ = C1
1 2 C2
Biểu thức nghiệm (2.5) bây giờ có thể viết dưới dạng
q = Ae−δt sin ωt + β (2.8)
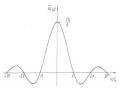
Từ biểu thức nghiệm (2.8) ta thấy: Khi lực cản đủ nhỏ, hệ thực hiện dao động tắt dần. Độ lệch Ae−δt giảm theo luật số mũ, tiệm cận tới không (hình 2.15). Dao động được mô tả bởi phương trình (2.8) là dao động họ hình sin.
Tuy chuyển động của hệ được mô tả bởi qui luật không tuần hoàn, nhưng toạ độ q lại đổi dấu một cách tuần hoàn. Vì thế người ta qui ước gọi 𝜔 là “tần số riêng”,
𝑇 = 2𝜋 𝜔 là “chu kỳ”, còn Ae−δt là “biên độ” của dao động tắt dần.
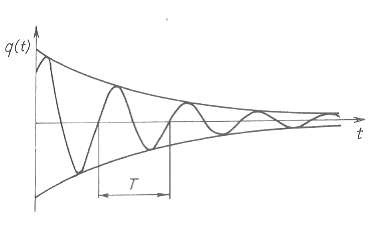
Hình 2.15 Đồ thị q trường hợp lực cản nhỏ
Để đặc trưng cho độ tắt dần của dao động tự do có cản nhớt, ta đưa vào khái niệm độ tắt lôga. Độ tắt lôga Λ được xác định bởi hệ thức
Λ ln
q(t)
q(t T)
δT
(2.9)
Độ tắt lôga đặc trưng cho độ giảm “biên độ” dao động tắt dần. Trong thực tế ta thường xác định tỷ số hai biên độ dao động sau k chu kỳ
Từ đó ta suy ra
q(t)
=
q(t + kT)
e−δt
e−δ(t+kT )
= eδkT
Λ δT 1 ln q(t)
k q(t kT)
b. Trường hợp thứ hai: 𝜹 > 𝝎𝟎 (lực cản lớn)
(2.10)
Khi 𝛿 > 𝜔0 hai nghiệm 𝜆1 và 𝜆2 của phương trình đặc trưng là các số thực và âm. Nghiệm tổng quát của phương trình vi phân dao động (2.3) có dạng
q Aeδtsh δ2 ω2 t β
(2.11)
0
Đường biểu diễn q = q(t) cắt trục t không quá một lần (hình 2.16). Do đó chuyển động của hệ là chuyển động tắt dần, không dao động.
c. Trường hợp thứ ba: 𝜹 = 𝝎𝟎 (lực cản tới hạn)
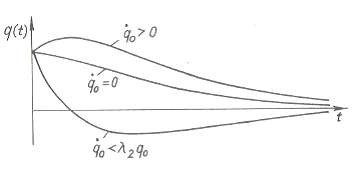
Hình 2.16 Đồ thị q trường hợp lực cản lớn
Trong trường hợp này hai nghiệm 𝜆1 và 𝜆2 là các số thực âm và bằng nhau.
Nghiệm tổng quát của phương trình vi phân dao động (2.3) có dạng
q = e−δt (C1t + C2) (2.12)
Chuyển động của hệ là tắt dần, không dao động.
Trong một số tài liệu viết về dao động trong kỹ thuật, người ta còn sử dụng khái niệm độ của Lehr. Độ cản Lehr (ký hiệu bằng chữ D) được xác định bởi hệ thức
D δ b b
(2.13)
mc
ω0 2mω0 2
Phương trình vi phân dao động tự do có cản nhớt (2.3) có thể viết dưới dạng
0
0
q + 2Dω0q + ω2q = 0 (2.14)
Do hệ thức ω2 − φ2 = ω0l − D2 chuyển động của hệ được phân thành ba
trường hợp sau:
D < l (δ < ω0 ) : độ cản nhỏ
D = l (δ = ω0) : độ cản tới hạn
D > l (δ > ω0 ) : độ cản lớn
Căn cứ vào độ cản Lehr ta có kết luận: Khi D < l chuyển động của hệ là dao động tắt dần, khi D ≥ 1 chuyển động của hệ tắt dần, không dao động.
Từ công thức định nghĩa độ cản Lehr, ta dễ dàng xác định được hệ thức liên hệ giữa độ tắt lôga và độ cản Lehr
l D2
Λ T 2D
(2.15)
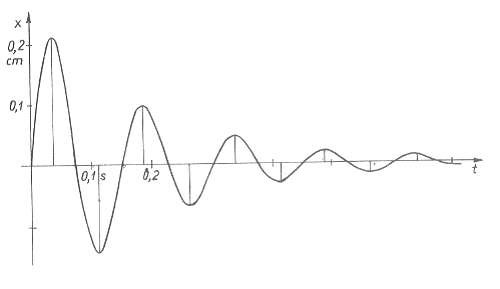
Thí dụ 2.9: Trên hình 2.17 là đồ thị dao động tịnh tiến thẳng của một vật điểm có khối lượng m = 0,5kg. Từ đồ thị dao động hãy xác định
- Chu kỳ và tần số dao động tắt dần
- Độ tắt lôga Λ
- Hệ số cản b và hệ số cứng c
- Các điều kiện đầu và qui luật dao động của vật điểm.
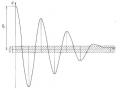
Lời giải: Từ đồ thị dao động ta thấy dao động của hệ là dao động tự do tắt dần với lực cản nhớt nhỏ. Thời gian thực hiện bốn chu kỳ dao động là 0,6s. Từ đó suy ra:
Chu kỳ dao động tắt dần
Hình 2.17 Hình thí dụ 2.9
T 0,6 s 0,15s
4
Tần số dao động tắt dần ω 2π 2π sl 41,9sl
T 0,15
Theo công thức (2.10) ta xác định độ tắt lôga
Λ = δT =
1 x(t)
ln
4 x(t + 4T)
1
= ln18,5 = 0,729 4
Từ đó suy ra
δ A0, 729 4,86sl T 0,15
Hệ số cản b của hệ có giá trị là
0
b = 2δm = 2 .4,86 .0,5 = 4,86 kg/s
Từ công thức ω = ω2 − δ2 ta tính được tần số dao động riêng của hệ
ω0 = ω2 + δ2 = 42,18s−l
Từ đó dễ dàng tính được hệ số cứng c
0
c = mω2 = 889,6 kg/s2
Từ đồ thị ta có ngay x(0) = 0. Với ký hiệu mx , mt là các tỷ lệ xích, 𝑡𝑔𝛼 là hệ số góc của tiếp tuyến với đường cong tại t = 0, ta có vận tốc ban đầu
x 0 = mx tgα = 10,5 cm/s mt
Qui luật dao động họ hình sin của hệ được xác định bởi công thức (2.8)
x t = v0e−δt sinωt = 0,25e−4,86t sin(41,9t) ω
Thí dụ 2.10: Cho biết các điều kiện đầu cho một hệ dao động trên hình 2.18 là x(0) = x0 , 𝑥 0 = 0. Hãy xác định năng lượng hao tán trong một chu kỳ. Cho biết D = 0,01.
Lời giải: Tại thời điểm đầu (t = 0), năng lượng của hệ dao động là
E0 = Π0 =
1 cx2
0
2
(do T0=0)
C2
m
Sau một chu kỳ năng lượng của hệ là
E1 = Π1 =
1 cx2
1
2
b
(do T1=0)
Từ biểu thức dao động tự do tắt dần ta có
x0 eδt x
x eδt
x
1 0
1
Do
2π 2π 2π
Hình 2.18 Hình
thí dụ 2.10
T = ==
0
ω
ta suy ra
ω2 − δ2
ω01 − D2
2πD
−
x1 = x0e
1−D2
Như thế, năng lượng hao tán trong một chu kỳ là
∆E = E0 − E1 =
1 cx2 −
0
2
1 cx2 e
0
2
4πD
−
1−D2 =
1 cx2 (1 − e
0
2
4πD
−
1−D2 )
Khi cho D = 0,01 thì
1 2 . Vậy sau chu kỳ đầu, năng lượng của hệ bị hao
tán mất 13%.
∆𝐸 = 0,13 . 𝑐𝑥
0
2
Thí dụ 2.11: Gắn một khối lượng m vào đầu thanh. Gắn vào thanh các phần tử cản và đàn hồi như hình 2.19. Bỏ qua khối lượng của thanh.
- Phải chọn độ lớn của hệ số cản b như thế nào để hệ có khả năng dao động nhỏ?
- Xác định độ cản Lehs D cần thiết để sau mười dao động., biên độ giảm còn 1/10 biên độ của chu kỳ đầu, sau đó xác định chu kỳ dao động.
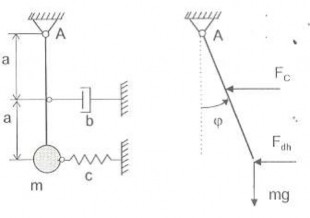
Hình 2.19 Hình thí dụ 2.11