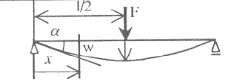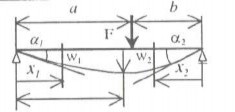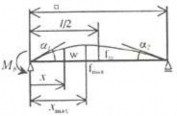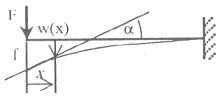
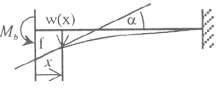
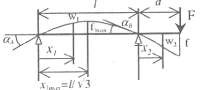
Bảng 3.1: Đỗ vòng và góc xoay của đường đàn hồi của các dầm thẳng có tiết diện không đổi.
Phương trình đường đàn hồi | Độ vòng | Góc xoay (tgα) | |
1 | w(x) = FI1 − 3x + 1x3 3EI 2I 2 I | 3 f= FI 3EI | 2 tgα = FI 2EI |
2 | w(x) = Mb I2x − 1 2 2EI I | 2 f = Mb I 2EI | tgα = Mb I EI |
3
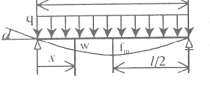
| w(x) = FI3 x1 − 3x2, x ≤ 1/2 16EI I 4 I | 3 f=FI 48EI | 2 tgα = FI 16EI |
4
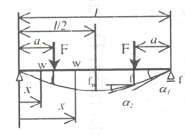
| 3 2 2 w (x ) = FI abx11 + 1 −x1, x ≤ a 1 1 16EI I I I b ab 1 w (x ) = FI3 ba2 x21 + 1 −x2, x ≤ b 2 2 2 16EI I I I a ab 2 | f= FI3a2b2 3EI I I f = f I+bI+b max 3b 3a | tgα = f 11 + 1 1 2a b tgα = f 11 + 1 2 2b a |
5 | 3 2 w (x ) = FI a x11 − x1, x ≤ 1 1 1 6EI I I I21 3 2 w (x ) = FI x22a + 3a . x2 − x2, x ≤ a 2 2 6EI I I I I I22 | f= FI3 a2 1 + a 3EI I I 3 f = FI a max 9I 3EI | 2 tgα = FI a A 6EI I tgαB = 2tgαA tgα = FI2 a (2 + 3a/I) 6EI I |
Có thể bạn quan tâm!
-
Dao động kỹ thuật - 9 -
Hình Bài Tập 2 Hình 2.46 Hình Bài Tập 3 -
Phương Pháp Sử Dụng Phương Trình Lagrange Loại Ii. -
Phương Pháp Giải Trực Tiếp (Ma Trận Cản Tùy Ý) -
Phương Pháp Ma Trận Dạng Riêng (Ma Trận Cản Đặc Biệt) -
A Mô Hình Dao Động Bộ Tắt Chấn Động Lực Có Tính Đến Ma Sát Nhớt
Xem toàn bộ 182 trang tài liệu này.
3 3 w (x )=FI1x1− a1 + ax1 + 1 1 2EI 3 I I I I aI21+23a I , x1≤a 3 w (x ) = FI a x2 (1 − x2)x ≤ 1 2 2 2EI I I I 2 | 3 2 f= FI a1 + 2a 2EI I 3I 3 f = FI a max 8EI I | 2 tgα = FI a1 + a 1 2EI I I 2 tgα = FI a 2 2EI I | ||||
7 | 3 2 w(x) = FI xa1 − a− 1xx ≤ a ≤ 1/2 2EI I I I 3 I 3 2 w(x) = FI ax1 − a− 1𝑎a ≤ x ≤ 1/2 2EI I I I 3 I | 3 2 f= FI a1 − 4a 2EI I 3I 3 2 f =FI a1 − 4𝑎 max 8EI I 3 I | 2 tgα = FI a1 − a 1 2EI I I 2 tgα = FI a1 − 2a 2 2EI I I | |||
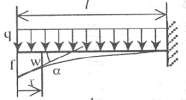
8 | 4 4 w(x) =qI1 − 4 x + 1𝑥 8EI 3 I 3 I | 4 f=qI 8EI | 3 tgα= qI 6EI | |||
9 | 4 2 3 w(x) = qI x1 − 2 𝑥+ 𝑥, 0 ≤ x ≤ 1 24EI I I I | f= | 5qI4 384EI | 3 tgα= qI 24EI | ||
10 | 2 w(x) = Mb I 6EI | 𝑥1 − x2 − x I I I xmax = I( 3 − 1)/ 3 | fm = fmax = | Mb I2 6EI Mb I2 9 3EI | 2 tgα = Mb I 1 3EI tgα = 1tgα 2 2 1 | |
6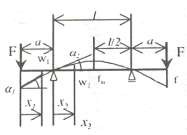 
3.2 DAO ĐỘNG TỰ DO KHÔNG CẢN
Phương trình vi phân dao độngtự do không cản của hệ n bậc tự do có dạng
M𝐪 + 𝐂 𝐪 = 𝟎 (2.1)
Trong đó M vàClà các ma trận vuông cấp n có các phần tử là hằng số. Trong nhiều bài toán thực tế, chúng là các ma trận thực đối xứng.
3.2.1 Các tần số riêng và các dạng dao động riêng
Ta tìm nghiệm của phương trình (2.1) dưới dạng
q = a sin(ωt +α) (2.2)
Thế biểu thức (2.2) vào phương trình (2.1) rồi đơn giản đi biểu thức sin(ωt +α) ta nhận được phương trình
(C – ω2M) a = 0 (2.3)
Để cho phương trìnhđại số tuyến tính thuần nhất (2.3) có nghiệm không tầm thường, điều kiện cần là
|C -ω2M| = 0 (2.4)
Phương trình (2.4) là một phương trình đại số bậc n đối với ω2 và được gọi là phương trình tần số hoặc phương trình đặc trưng. Các nghiệm ωk (k = 1, …n) của phương trình tần số được gọi là các tần số riêng. Thay lần lượt các giá trị của ωk (k = 1,
…, n) vào phương trình (2.3) ta nhận được các phương trình đại số tuyến tính thuần nhất để xác định các thành phần của véc tơ ak
k
(C-ω2 M )ak= 0 (2.5)
Các véc tơ ak này được gọi là các véc tơ riêng.
Do phương trình (2.5) là hệ phương trìnhđại số tuyến tính thuần nhất cóđịnh thức hệ số bằng không nên các thành phần của véc tơak được xácđịnh sai khác một hệ số nhân. Chẳng hạn ta có thể chọna1k một cách tùyý.
v
Ta đưa vào ký hiệu
vik =
aik a1k
hoặc
(k ) i
(k )
a
a
i(k ) 1
i, k = 1,2 … , n (2.6)
Thay lần lượt các ω1 , ω2 , ….ωn vào phương trình (2.5) tá xácđịnhđược ma trận.
v11
v12
... v1n
v v ... v
V =
21 22 2n
(2.7)
... ... ... ...
v v ... v
n1 n2 nn
Mỗi véc tơ cột của ma trận (2.7)
Vk = [v1k v2k ... vnk]T = [v(k), v(k), … . v(𝑘)]T
1 2 𝑛
Cho ta biết một dạng dao động riêng của hệ dao động (2.1). Ma trậnVđược gọi làma trận riêng (Modalmatrix). Như thế ma trận dạng riêng cho ta biết tất cả các dạng dao động riêng có thể có của hệ dao động.
Xét trường hợp hệ hai bậc tự do. Khi đó các phương trình vi phân dao động tự do không cản có dạng.
m11 m12 11 12 1 0
q 1c cq= (2.8)
m21 m22 q 2 c21 c22 q2 0
Phương trình tần số (2.4) đối với trường hợp này có dạng.
c11 − ω2m11 c12 − ω2m12
c21
− ω2m21
c22
− ω2m22
Khai triểnđịnh thức cấp hai trên ta được
(c11- ω2m11)(c22- ω2m22) - (c12- ω2m12)(c21- ω2m21) = 0 (2.9)
Nếu ta đưa vào ký hiệu vi = a(i)a(i)
thì từ phương trình (2.5) ta suy ra các
2 1
phương trình xácđịnh các phần tử của ma trận dạng riêng
(c11- ω2m11) + vi (c12- ω2m12) = 0 i = 1, 2 (2.10a)
i i
hoặc
(c21- ω2m21) + vi (c22- ω2m22) = 0 i = 1, 2 (2.10b)
i i
Ma trận dạng riêng của hệ hai bậc tự do trên có dạng
V= 1 1
v2 v2
Thí dụ 3.6: Cho mô hình dao động như hình vẽ 3.6a. Hãy xác định ma trận dạng riêng khi c1 = c2 = c, m1 = m2 = m, sau đó vẽ các dạng dao động riêng của hệ.
q1
q2
c1
c2
m1
m2
Hình 3.6 Hình thí dụ 3.6
Lời giải: Biểu thức động năng và thế nâng của hệ có dạng.
T = = 1 m q 2 + 1 m q 2
2 1 1 2 2 2
Π = 1 c q2 + 1 c (q – q )2
2 1 1 2 2 2 1
Sử dụng phương trình Lagrange loại II, ta dễ dàng thiết lập đượcphương trình vi phân dao động tự do của hệ
c1 + c2 − c2 q1 0
m1 0q 1+ = (2.11)
0 m2
q 2
−c2 c2 q2 0
Tương ứng với phương trình (2.3) ta có
0
c1 + c2 − c2− ω2m1 0a1= (2.12)
−c2 c2
0 m2
a2 0
Từ đó ta suy ra phương trình tần số
c1 + c2 − ω2m11 − c2
c2 c2 − ω2m2
= 0 (2.13)
Khai triển định thức (2.13) ta được phương trình
4 c1 c2 c2
ω2
c1c2 0
m m m m
1 2 1 2
Từ đó ta tính được các tần số riêng
1 c c c
4 m1
1 221 2
2
c c
m2
m1m2
1 c c c
ω2
1 22
(2.14)
1,2
2 m m
1 2
Thế các biểu thức củaω1 và ω2 vào phương trình (2.12) ta có
a = a11= 1 a = 1 a
1
1
1 a21
(c1 + c2 − m1ω2)/c2 11
c2/(c2 − m2 ω2) 11
a = a12= 1 a = 1 a
2
2
2 a22 (c1 + c2 − m1ω2)/c2 12 c2/(c2 − m2ω2) 12
Trong đó các đại lượng a11 và a12 là các hằng số chọn tùy ý. Khi c1 = c2 = c và m1 = m2 = m, ta dễ dàng tính được.
V v11
v12 1 1
v21
v22 1,62 0,62
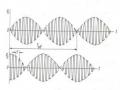
Trên hình 3.6b cho ta tác dụng dao động riêng thứ nhất và thứ hai.
q1
q2
c1
c2
m1
m2
v11 v21
v12
v22
Dao đoäng rieâng thöùnhaát
Dao đoäng rieâng thöùhai
Hình 3.6b Các dạng dao động riêng
3.2.2 Tính chất trực giao của các véc tơ riêng
Xét phương trình vi phân dao động tự do không cản của hệ n bậc tự do
M𝐪 + 𝐂 𝐪 = 𝟎 (2.15)
Nếu các ma trận khối lượng M và ma trận độ cứng C là các ma trận thực đối xứng thì các véc tơ riêng vk tương ứng với các tần số riêng ωk sẽ trực giao với ma trận khối lượng M và ma trận độ cứng C. Ta có các hệ số
𝐯T 𝐌 𝐯i = 0; 𝐯T 𝐂 𝐯i = 0 khi ωi ≠ ωj (2.16)
j j
Ta sẽ chứng minh tính chất trên. Chú ý đến ký hiệu (2.6), từ phương trình (2.5) ta suy ra
i
ω2𝐌 𝐯i = 𝐂 𝐯i (2.17)
i
ω2𝐌 𝐯i = 𝐂 𝐯i (2.18)
Nhân bên trái từ phương trình (2.17) với 𝐯T phương trình (2.18) 𝐯T ta được
j i
ω2𝐯T 𝐌 𝐯i = 𝐯T 𝐂 𝐯i (2.19)
i j j
ω2𝐯T 𝐌 𝐯j = 𝐯T 𝐂 𝐯j (2.20)
j i i
Do tính chất đối xứng của các ma trận M và C ta có
𝐯T 𝐌 𝐯i = 𝐯T 𝐌 𝐯j ; 𝐯T 𝐂 𝐯i = 𝐯T 𝐂 𝐯j (2.21)
j i j i
Đem phương trình (2.19) trừ đi phương trình (2.20) và chúý đến tính chất (2.21) ta suy ra.
(ω2−ω2 𝐯T 𝐌 𝐯i = 0 (2.22)
i j j
Do đó 𝐯T 𝐌 𝐯i = 0 khi ωi ≠ ωj . Từ 2.19 ta suy ra 𝐯T 𝐂 𝐯i = 0 khi ωi ≠ ωj
j j
Chú ý rằng nếu ω2 = ω2 thì từ (2.22) ta không thể suy ra tính chất trực giao
i j
của các véc tơ riêng tương ứng.
i
Giả sử ω2 là một nghiệm bội k củaphương trình đặc trưng. Do M = MT , C = CT
i
nên ứng với ω2 ta sẽ có k véc tơ riêng độc lập tuyến tính. Các véc tơ trực giao với (n-
i
k) véc tơ riêng còn lại. Mỗi tổ hợp tuyến tính của k véc tơ riêng này lại là một véc tơ riêng tương ứng với ω2. Như thế từ k véc tơ riêng nàyta có thể xây dựngmột cơ sở trực giao đối với M của không gian con của Rn. Xây dựng tương tự đối với các trị riêng bội khác của phương trình đặc trưng, kết quả ta được n véc tơ riêng trực giao với M.
3.2.3 Các tọa độ chính
Như trên đã trình bày, phương trình vi phân dao động tự do không cản của hệ n bậc tự do có dạng
M𝐪 + 𝐂 𝐪 = 𝟎 (2.23)
Nếu ta có thể chọn được các tọa độ suy rộng đặc biệt sao cho các tọa độđó, các ma trận khối lượng và ma trận cứng đều có dạng đường chéo, thì các tọa độ suy rộngđó được gọi là các tọa độ chính. Ta ký hiệu các tọa độ chính bởi p1, p2, ….pn
Thực hiện phép đổi biến
q = V p (2.24)
Trong đó V là ma trận dạng riêng. Thế (2.24) vào phương trình (2.23) ta có
M V 𝐩 + C V p = 0
Nhân bên trái phương trình trên với VT ta được
VTM V𝐩 + VTC V p = 0 (2.25)
Do tính chất (2.16) các ma trận VTM V và VTC V là các ma trận đường chéo
μ1 0 … 0 γ1 0 … 0
𝐕𝐓𝐌 𝐕 = 0 μ2 … … ; 𝐕𝐓𝐂 𝐕 = 0 γ2 … …(2.26)
… … … …
0 … … μn
Vì vậy các phương trình (2.25) có dạng
… … … …
0 … … γn
µi p i + 𝛾ipi = 0 i = 1,2,…,n (2.27) Trong đó :
µi = 𝐯T M vi ; γi = 𝐯T C vi (2.28)
i i
Nếu đưa vào các ký hiệu
ω2 γi
(2.29)
μ
i
i
thì các phương trình (2.27) xác định các dao động chính có dạng
i
p i + ω2 pi i = 1,2,…,n (2.30) Việc giải các phương trình (2.30) đã được bàn kỹ trong chương 2.
Thí dụ 3.7: Một hệ hai con lắc có chiều dài mỗi thanh là 1, khối lượng mỗi vật điểm là m. Hai thanh được nối với nhau bằng lò xo có hệ cứng là c, ở vị trí cách trục quay một đoạn là d (xem hình 3.7). Độ dài của lò xo ở trạng thái không biến dạng bằng khoảng cách giữa hai trục con lắc. Bỏ qua khối lượng các thanh, khối lượng lò xo và lực cản.
a. Xác định các tọa độ chính của hệ.
b. Xác định doa động tự do của hệ với các điều kiện đầu φ1(0) = φ(),φ2(0) = 0,
φ 1(0) = 0, φ 2(0) = 0
d
c
l
1
2
1
h2
h
Hình 3.7 Hình thí dụ 3.7
Lời giải: Trước hết ta thiết lập phương trình vi phân dao động tự do của hệ hai con lắc trên hình 3.7. Biểu thức động năng và thế năng có dạng
T 1 ml2φ&2 φ&2
2
Π mgh
1 2
mgh
1 cd2 φ
φ 2
1 2 2 2 1
Do h l1 cos cos φ 1 lφ2
1 1 21
h l1 coscos φ 1 lφ2
2 2 2 2
nên ta có
Π 1mgl cd2φ2 φ2 2cd2φ φ
2 1 2 1 2
Thế các biểu thức động năng, thế năng và phương trình Lagrange loại II ta được các phương trình dao động tự do hệ hai con lắc
ml2φ 1 + mgl + cd2 φ1 − cd2φ2 = 0 ml2φ 2 − cd2φ1 + mgl + cd2 φ2 = 0
Ở thí dụ này ta có m11 = m22 = ml2, m12 = 0, m21 = 0, c11 = c22 = mgl + cd2, c12 =
c21 = - cd2. Do đó phương trình tần số có dạng
(mgl + cd2 – ml2ω2)2 – c2d4 = 0 Từ đó suy ra
1
ω2 = g
l
; ω2 =
g 2cd2 l + ml2
2
Bây giờ ta xác định các phần tử của ma trận dạng riêng. Từ phương trình (2.10a) ta suy ra
c m ω2
mgl cd2 ml2 g
v1
11 11 1
1
c12 m12ω2
l 1
cd2
mgl cd2 ml2 g2cd2
c m ω2
l ml2
v2
11 11 2
2
c12 m12ω2
1
cd2
Vậy ma trận dạng riêng là
V = 1 1
1 −1
Từ đó ta có
φ1 = p1 + p2 φ2 = p1 − p2
→ p1 = φ1 + φ22 p2 = φ1 − φ22
Phương trình dao động dạng tọa độ chính
1
2
p 1 + ω2p1 = 0 p 2 + ω2p2 = 0
Từ đó ta dễ dàng tìm được các dạng dao động chính