Phương Pháp Sử Dụng Phương Trình Lagrange Loại Ii.

Chương 3

DAO ĐỘNG TUYẾN TÍNH CỦA HỆ NHIỀU BẬC TỰ DO

Cũng như trong chương 2, ở đây ta chỉ xét dao động của các hệ cơ học hôlônôm. Một hệ n bậc tự do là một hệ mà vị trí của nó trong không gian được xác định bởi n tọa độ suy rộng: q1, q2, …qn. Dưới tác dụng của lực, chuyển động của hệ được xác định bởi sự biến đổi của các tọa độ suy rộng này theo thời gian.

Trong chương này ta xét bài toán dao động nhỏ của hệ n bậc tự do quanh vị trí cân bằng tĩnh. Khi đó hệ các phương trình vi phân mô tả dao động của hệ là hệ n phương trình vi phân tuyến tính cấp hai hệ số hằng số.

Trong các bài toán kỹ thuật, ta thường gặp bốn mô hình cơ học sau: hệ các vật rắn, hệ các vật rắn, hệ các phần tử hữu hạn, hệ liên tục, hệ nhiều vật hỗn hợp. Các phương trình toán học mô tả dao động của hệ các vật rắn là các phương trình vi phân thường, loại phương trình chúng ta xét trong chương này. Đối với các phần tử hữu hạn, sau một số phép biến đổi ta cũng nhận được các phương trình vi phân thường. Các phương trình toán học mô tả dao động của hệ liên tục (môi trường liên tục) là các phương trình đạo hàm riêng. Các phương trình toán học mô tả dao động của hệ nhiều vật hỗn hợp là các phương trình vi phân thường và các phương trình đạo hàm riêng. Tuy nhiên, khi tính toán dao động của các hệ phức tạp, người ta thường cố gắng biến đổi tương đương gần đúng về hệ n tự do, với n là số bé nhất có thể chấp nhận được.

3.1 THÀNH LẬP CÁC PHƯƠNG TRÌNH VI PHÂN DAO ĐỘNG

Việc lựa chọn các phương pháp để thành lập các phương trình vi phân dao động của hệ nhiều bậc tự do vào mô hình cơ học của các máy và các công trình. Đối với các hệ cơ gồm các chất điểm, các vật rắn, các phần tử lò xo bỏ qua trọng lượng, các phần tử cản, người ta thường dùng phương trình Lagrange loại hai để thiết lập các phương trình dao động. Đối với các kết cấu đàn hồi, người ta thường sử dụng các phương pháp lực, phương pháp biến dạng, phương pháp phần tử hữu hạn. Đối với các hệ cơ phức tạp người ta còn sử dụng phương pháp các hệ con (phương pháp tách cấu trúc) để thiết lập các phương trình vi phân dao động. Dưới đây ta trình bày việc áp dụng phương pháp sử dụng phương trình Lagrange loại hai và phương pháp lực thiết lập phương trình vi phân dao động của một số mô hình dao động cụ thể.

3.1.1 Phương pháp sử dụng phương trình Lagrange loại II.

Có thể bạn quan tâm!

• Đồ Thị Biểu Diễn Sự Phụ Thuộc Của Góc 𝛹 Vào 𝜂
• Dao động kỹ thuật - 9
• Hình Bài Tập 2 Hình 2.46 Hình Bài Tập 3
• Đỗ Vòng Và Góc Xoay Của Đường Đàn Hồi Của Các Dầm Thẳng Có Tiết Diện Không Đổi.
• Phương Pháp Giải Trực Tiếp (Ma Trận Cản Tùy Ý)
• Phương Pháp Ma Trận Dạng Riêng (Ma Trận Cản Đặc Biệt)

Xem toàn bộ 182 trang tài liệu này.

Các phương trình Lagrange loại II được áp dụng để thiết lập các phương trình vi phân chuyển động của hệ hôlônôm có dạng tổng quát như sau:

dTT

 Q i  1,, n

(1.1)



i 

dt q 

qi

i

Trong đó: qi là tọa độ suy rộng, Qi là lực suy rộng, T là biểu thức động năng, n là số bậc tự do của hệ.

Thí dụ 3.1: Cho mô hình dao động như hình vẽ 3.1. Hãy thiết lập phương trình vi phân dao động của hệ.

q1

q2

b1

b2

c

1

m

1

c

F(t)

2

m

2

Hình 3.1 Hình thí dụ 3.1

Lời giải: Biểu thức động năng và thế năng của hệ có dạng

T 1 m q&21 m q&2

2 1 1

1

Π =2

2 2 2

1

2

c1q1 + c2

2 2

Biểu thức hàm hao tán có dạng

q2 − q1

Φ = 1 2 12

m1q 1 + b2 2 2

q 2 − q 1

Thế các biểu thức trên vào phương trình Lagrange loại II

d ∂T ∂T

−

∂π ∂Φ

= − −

+ Q∗

dt ∂q i

∂qi

∂qi

∂q i i

ta nhận được hệ phương trình dao động

m1q + (b1+b2)q 1 - b2q 2 + (c1+c2)q1 - c2q2 = 0

m2q 2 - b2q 1 + b2q 2 – c1q1 + c2q2 = F(t) (1.2) Các phương trình (1.2) có thể viết dưới dạng ma trận như sau:

Mq + Bq + Cq = f (t) (1.3)

Trong đó

M = 𝑚1 0, B = b1 + b2 −b2

0 𝑚2 −b2 b2

C = c1 + c2 −c2, q = q1, f = 0

−c2 c2 q2

F(t)

Khi hệ không có lực kích động và không có phần tử cản, phương trình dao động tự do không cản có dạng

0

𝑚1 0q 1+ c1 + c2 − c2q1= (1.4)

0 𝑚2

q 2

−c2 c2 q2 0

Thí dụ 3.2: Thiết lập phương trình dao động xoắn của một mô hình chuyển động như hình 3.2. cho biết các moomen M1 (t), M4 (t). Các mômen M2 và M3 tỷ lệ với vận tốc.

M2 = -b2φ 2 , M3 = -b3 φ 3

M1(t)

J1 J2

c1

M2 r2

r3

J4 M4(t)

c

2

M3

J3

Hình 3.2 Hình thí dụ 3.2

Lời giải: Cơ cấu truyềnđộng như hình 3.2 là một hệ dao động ba bậc tự do. Trong bốn đại lượng định vị φ1, φ2, φ3 , φ4 có một điều kiện ràng buộc r2φ2 = - r3φ3. Ta chọn các tọa độ suy rộng: q1 = φ1, q2 = φ2, q3 = φ4 . Động năng và thế năng của hệ có dạng

1 1

T = 1(J φ 2

2

+ J2φ 2 + J3φ 23 + J4φ 2 )

2 4

Π = 1c (φ - φ )2+ 1 c (φ - φ )2

2 1 2 1 2 2 4 3

Thế điều kiện ràng buộc φ = - r2φ

vào các biểu thức trên, ta có

3 r3 2

T = 1{J φ 2

+ [J

+ (r2 )2 J ]φ 2

+ J φ 2 }

2 1 1

2 r33

2 4 4

Π = 1c (φ - φ )2+ 1 c (φ

+ r2 φ )2

2 1 2 1

2 2 4

r3 2

Để xác định các lực suy rộng ứng với các lực khống chế, ta tính công khả dĩ của

hệ

δA = M1 (t)δφ1 + M2 (t)δφ2 + M3 (t)δφ3 + M4 (t)δφ4

= M (t)δφ

+ b φ

δφ -b (r2)2 φ

δφ + M

(t)δφ

1

Vậy ta có

1 2 2

2 3 r3 2 2 4 4

Q

1

* = M1

(t) , Q*

= - [b2

+ b (r2)2 ]φ

3

r3

2 , Q*

= M4

(t)

2

3

Thế các biểu thức động năng, thế năng và lực suy rộng ứng với các lực không có thế vào phương trình Lagrange loại II

d ∂T ∂T

−

= − ∂Π + Q∗

dt ∂q k ∂qk

∂qk k

Ta nhận được hệ phương trình vi phân dao động của cơ cấu truyền động J1φ1 – c1(φ2 – φ1) = M1 (t)

[J2 + (r2/r3)2 J3]φ 2 + [b2 + b3(r2/r3)2]φ 2

r

+ c (φ - φ )+ c r2(φ

+r2φ ) = 0 (1.5)

J φ + c r2(φ

1 2 1

+r2φ ) = M (t)

2 3 4 r3 2

4 4 2

r3

4 r3 2 1

Hệ phương trình (1.5) có thể viết dưới dạng ma trận như sau

M 𝐪 + B𝐪 + Cq = f(t) (1.6)

Trong đó

J1 0 0

0 0 0

M = 0 +(r2r3)2J3 0 , B = 0 b2 + (r2r3)2b3 0

0 0 J4

0 0 0

c1 0 0

φ1 M1(t)

C =−c1

c1 + (r2

r3

)2c2

r2

r3 c2

, q = φ2

φ

f= 0

0 0 c2

4 M4(t)

Thí dụ 3.3: Thiết lập phương trình vi phân dao động tự do của hệ dao động xoắn gồm n đĩa như hình 3.3

n-n

c1

c2

cn-2 cn-1

J1 J2 Jn-1 Jn

Hình 3.3 Hình thí dụ 3.3

Lời giải: Biểu thức động năng và biểu thức thế năng của hệ có dạng

T = 1𝑛 J φ 2

2 𝑖=1 𝑖 i

Π = 1𝑛 −1 c

(𝜑

– φ )2

2 𝑖=1 𝑖

i+1 i

Thế các biểu thức động năng và thế năng trên vào phương trình Lagrange loại II

d ∂T ∂T



−

i

dt ∂φ i ∂

∂Π

= −

∂φ i

Ta được hệ phương trình dao động tự do của mô hình khảo sát J1φ 1+ c1 (𝜑1 – φ2) = 0

J2φ 2 + c2 (𝜑2– φ3) – c1 (𝜑1– φ2) = 0

………………………………………. (1.7) Jn-1φ n-1 + cn-1 (𝜑n-1 – φn) – cn-2 (𝜑n-2– φn-1) = 0

Jnφ n + cn-1 (𝜑n-1 – φn) = 0

Hệ phương trình (1.7)có thể viết dưới dạng ma trận

M 𝐪 + C q = 0

Thí dụ 3.4: Một móng khối thẳng có khối lượng m tựa trên các lò xo theo hai phương thẳng đứng và nằm ngang, chịu tác dụng của lực F(t) thẳng đứng (hình3.4a). Hãy thiết lập phương trình dao động nhỏ của móng khối phẳng quanh vị trí cân bằng tĩnh. Giả thiết rằng móng chỉ chuyển động trong mặt phẳng hình vẽ vàở vị trí như hình vẽ 3.4a các lò xo chưa bị kéo nén.

e

m,Jc

y



cx1

cy1

C

x

A

B

m

cx2

cy2

a1a2

F(t)

y

2 2



x

b

I

1

y

I

1

1

Ix +Ix

A

A'

1

Iy +Iy

x B'

B

y

2

2

I Ix

1

Iy +Iy

Ix +Ix

1 1 1

a) b)

Hình 3.4 Hình thí dụ 3.4

Lời giải: Vị trí của móng được xácđịnh bởi vị trí trọng tâm của nó x,y và các góc xoay φ. Hệ tọa độ được chọn sao cho ở thờiđiểm ban đầu t= 0 thì x=0, y = 0 và φ

= 0.

Biểu thức động năng của móng máy

T = 1m ( x&2y&2)2+ 1J φ 2

2 2 c

Khi móng máy dao động trong mặt phẳng, biến dạng dài của các lò xo làΔlx1 , Δlx2 , Δly1 , Δly2 ( hình 3.4b). Thế năng của hệ có dạng

x1

Π = mgy + 1(c

2

Δl2x1

+ cx2

Δl2x2

+ cy1

Δl2y1

+ cy2

Δl2y2

) (1.9)

Chúng ta ký hiệu các thành phần dịch chuyển từ điểm A ( từ A đến A’) là u1 và v1, các thành phần dịch chuyển từ điểm B (từ B đến B’)là u2 và v2. Theo hình vẽ 3.4b ta có

u1= x + a1(1-cos φ) + bsinφ; v1 = y - a1sinφ + b(1-cos φ)

u2 = x – a2(1-cos φ) + bsinφ ; v2 = y + a2sinφ + b(1-cos φ)

Từ định lý hàm consin trong lượng giác ta tính được

Δl2x1 = l2x1 [ 1 + (u2 + v2 + 2lx1u1)/l2 − 1]2

1 1 x1

Δl2y1 = l2y1 [ 1 + (u2 + v2 + 2ly1 v1)/l2 − 1]2

1 1 y1

Δl2x2 = l2x2 [ 1 + (u2 + v2 + 2lx2u2)/l2 − 1]2

2 2 x2

Δl2y2 = l2y2 [ 1 + (u2 + v2 + 2ly2 v2)/l2 − 1]2

2 2 y2

Cácđại lượng lx1, lx2 , ly1, ly2 là độ dài các lò xo ở trạng thái chưa biến dạng. Do chúng ta chỉ xét dao động nhỏ xung quanh vị trí cân bằng nên có thể sử dụng các xấp xỉ sau.

Δl2x1 ≈ u2; Δl2x2 ≈ u2; Δl2y1 ≈ v2 ; Δl2y2 ≈ v2

1 2 1 2

Do góc φ nhỏ, ta lấy xấp xỉ sinφ≈φ, cosφ ≈ 1. Từ đó ta tính được Δl2x1 ≈ x + bφ 2 ; Δl2y1≈ (y − a1φ)2

Δl2x2 ≈ x + bφ 2 ; Δl2y2 ≈ (y + a2φ)2

Biểu thức gần đúng của thế năng Π có dạng

Π = 1[c

(x - bφ)2+ c

(x- bφ)2+ c y − a

φ 2+ c

y + a

φ 2] + mgy

2 x1

x2 y2 1

y2 2

Để xácđịnh các lực suy rộngứng với lực F (t) ta tính công khả dĩ của hệ δA = -F(t)δy - F(t)eδφ

Từ đó ta suy ra

Q* * *

x = 0 ; Q y = - F(t) ; Q φ = - F(t)e

Thế các biểu thức động năng, thế năng, lực suy rộng ứng với lực không có thế vào phương trình Lagrange loại II

d T T

Π Q*

dt q& q q i

i i i

ta có phương trình vi phân của móng máy khảo sát

M 𝐪 + C q = f(t) (1.10)

với

m 0 0 x 0

M = 0 𝑚 0; q = y; f= − mg + F

0 0 Jc φ eF

C =

cx1 + cx2 0 (cx1 + cx2)b

0 cy1 + cy2 a2cy2 − a1cy1

(cx1 + cx2)b a2cy2 − a1cy1 [(cx1 + cx2)b2 + a2cy1 + a2 cy2]

1 2

3.1.2 Phương pháp lực

Phương pháp lực hay được sử dụng để thiết lập các phương trình dao động của các hệ thanh có khối lượng tập trung. Để thấy rò nội dung của phương pháp này, trước hết ta xét một thí dụ. Sau đó trình bày quy trình tổng quát áp dụng phương pháp lực thiết lập các phương trình vi phân dao động.

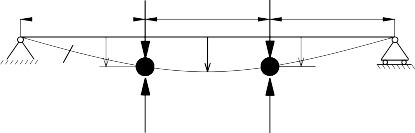
Thí dụ 3.5: Thiết lập các phương trình vi phân dao động của dầm không trọng lượng mang hai khối lượng tập trung m1, m2 và chịu các lực tác dụng F1, F2 như hình vẽ 3.5. Cho biết m1 = 2m, m2 = m.

F1 F2

a a a

q q2

1

m

m

EI

1 2

m q.. m q..

1 1 2 2

Hình 3.5 Hình thí dụ 3.5

Lời giải: Theo định luật Hooke suy rộng ra ta có các hệ thức liên hệ giữa dịch chuyển và lực (hình 3.5)

q1 = d11F∗ +d12F∗

1 2

q2= d21F∗ +d22F∗ (1.11)

1 2

1

2

trong đó F∗ = F1 – m1q1 F∗ = F2 – m2q2

Trong (1.11) dij = dji là các hệ số ảnh hưởng. Trong giáo trình sức bền vật liệu [6,7] người ta đã đưa ra định nghĩa và cách xác định các hệ số này. Bảng 3.1 cho ta cách tính độ vòng của một số loại dầm thẳng chịu tác dụng của các dạng lực cơ bản. Từ đó dễ dàng xác định các hệ số ảnh hưởng dij.

Các hệ số ảnh hưởng dij lập thành một ma trận gọi là ma trận hệ số ảnh hưởng

hoặc ma trận độ mềm xác định như sau:

D =d11 d12

d21 d22

Từ bảng 3.1 dễ dàng tính được độ lớn của các hệ sốảnh hưởng đối với dầm trên hình 3.5. Phương trình (1.11) bây giờ có dạng

q1= q2

a3 8 7

18EI 7 8

F∗

F

∗

1(1.12)

2

i

Khi dầm dao động quanh vị trí cân bằng tĩnh, các lực tác dụngF∗ bao gồm lực

quán tính - miq i và ngoại lực Fi (t). Ta có hệ thức.

f* =

1= − m1

0 q 1+

F1 (1.13)

F

F∗

2

∗ 0 m2 q 2 F2

Thế biểu thức (1.13) vào (1.12) ta nhậnđược phương trình uốn của dầm

ma316 7&q&1q1

a3 8F1

7F2 

18EI 14 8&q&

q 

18EI 7F 8F 

(1.14)



2 

2 

1 2 

Từ thí dụ trên ta có thểđưa ra một nguyên tắc chung áp dụng phương pháp lực để thiết lập phương trình vi phân dao động. Đầu tiên ta viếtđịnh luật Hook suy rộng

q = Df* (1.15)

Sau đó sử dụng quan hệ giữa lực và gia tốc

f* = - M𝐪 + 𝐟 (1.16)

Thế (1.16) vào phương trình (1.15) ta nhậnđược phương trình vi phân dao động

DM𝐪 + 𝐪 = 𝐃 𝐟 (1.17)

Chúý rằng ma trận độ cứng C và ma trận độ mềm D của hệ dao động có quan hệ như sau

C-1 = D (1.18)

Đối với hệ cơ học phức tạp, ngày nay ngoài hai phương pháp trên người ta còn sử dụng phương pháp tách cấu trúc để thiết lập phương trình vi phân dao động.