Đồ Thị Biểu Diễn Sự Phụ Thuộc Của Góc 𝛹 Vào 𝜂

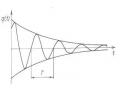
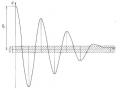
Ta xét trường hợp khi tần số Ω của lực kích động rất gần với tần số dao động tự do 𝜔0. Đưa vào ký hiệu

Ω − ω0 = 2ε

trong đó ε là một đại lượng vô cùng bé. Bỏ qua các số hạng bé cỡ ε trong biểu thức của q ta có

h

0

0

q ≈ sinΩt − sinω

2h

t =

Ω + ω0 Ω − ω0

Có thể bạn quan tâm!

• Xác Định Các Tham Số Độ Cứng Của Hệ Dao Động
• Tính Toán Dao Động Tự Do Có Ma Sát Nhớt
• A Đồ Thị Dao Động Tự Do Có Ma Sát Khô Với Điều Kiện Đầu 𝑡 = 0 ∶
• Dao động kỹ thuật - 9
• Hình Bài Tập 2 Hình 2.46 Hình Bài Tập 3
• Phương Pháp Sử Dụng Phương Trình Lagrange Loại Ii.

Xem toàn bộ 182 trang tài liệu này.

cos t sin t

ω2 − Ω2 0 ω2 − Ω2 2 2

 2h sinεtcos Ω  ω0 t hsinεt cosΩt

(3.17)

0

ω2  Ω2

2 2Ωε

Do ε là một đại lượng vô cùng bé nên hàm sinεt biến thiên chậm, còn chu kỳ của nó 2π ε rất lớn. Trong trường hợp này có thể xem biểu thức (3.17) là qui luật dao động với chu kỳ 2π Ω và biên độ biến đổi 𝑕 2Ω𝜀 𝑠𝑖𝑛𝜀𝑡. Dạng dao động này được biểu diễn trên hình 2.24. Hiện tượng dao động này gọi là hiện tượng phách.

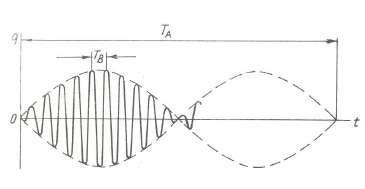
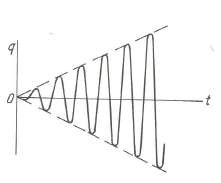
Hình 2.24 Hiện tượng phách Hình 2.25 Đồ thị q(t)

Xét trường hợp Ω → ω0(ε → 0). Khi đó, ta có thể thay sinεt bằmg εt trong biểu thức (3.17) và ta có hệ thức

q ht

2ω0

cos ω0t

(3.18)

Biên độ 𝑕𝑡/2𝜔0 tăng lên vô hạn khi thời gian t tăng như hình 2.25. Như thế, ngay trong phạm vi lý thuyết dao động tuyến tính không cản, sự tăng biên độ lên vô hạn ở vùng cộng hưởng cũng đòi hỏi phải có thời gian. Đối với các máy được thiết kế làm việc ở trên vùng cộng hưởng, khi tăng vận tốc của máy qua vùng cộng hưởng, cần phải khẩn trương cho vượt qua đủ nhanh.

Như thế khi tính toán dao động cưỡng bức không cản ta phân ra hai trường hợp:

- Trường hợp xa cộng hưởng Ω ≠ 𝜔0

- Trường hợp gần cộng hưởng Ω ≈ 𝜔0. Trong trường hợp này khi Ω = ω0 + 2ε ta có hiện tượng phách, khi Ω = 𝜔0ta có hiện tượng cộng hưởng.

Thí dụ 2.12: Bánh xe O lăn không trượt trên mặt đường gồ ghề lượn sóng. Vận tốc tâm O của bánh xe luôn không đổi là v = 60km/h. Mặt đường lượn sóng có phương

trình là s = s sin πxvới s = 2cm , L = 100cm. Xác định biên độ dao động cưỡng

L

bức thẳng đứng của vật thể M có khối lượng m, nối với trục bánh xe bằng lò xo có độ cứng là c. Biết rằng biến dạng tĩnh của lò xo dưới tác dụng của vật thể là δ0 = 10cm.

Lời giải: Từ điều kiện cân bằng tĩnh cδ0

= mg ta suy ra c= mg

δ0

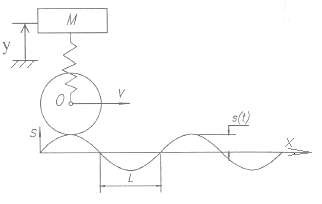
Hình 2.26 Hình thí dụ 2.12

Phương trình vi phân chuyển động của vật thể M có dạng

my + c y − s = 0

Nếu đưa vào ký hiệu 𝜔2 = 𝑐

, phương trình vi phân dao động được đưa về

dạng

0 𝑚

y + ω2y = ω2s sin πx

Biến đổi

0 0 L

ω2 = c = mg = g

= 98,1 1 s2

0 m

πx πvt

mδ0 δ0

πv 16,6π

= = Ωt , với Ω = =

L L L 1

= 16,6π

Khi đó nghiệm riêng của phương trình trên là

y = AsinΩt

với

0

ω2s

A = =

ω2 − Ω2

s

Ω2 =

2

16,6π 2

= 0,075cm

01 −

ω0

1 −

98,1

c. Tính toán dao động cưỡng bức có ma sát nhớt

Các phương trình vi phân dao động tuyến tính chịu kích động điều hoà của hệ một bậc tự do có ma sát nhớt (3.6), (3.7) có thể viết dưới dạng như sau

0

q + 2δq + ω2q = h1sinΩt + h2cosΩt (3.19)

Ta tìm nghiệm riêng của phương trình này dưới dạng

q∗t = MsinΩt + NcosΩt (3.20)

Trong đó M, N là các hằng số cần xác định. Thế biểu thức (3.20) vào phương trình (3.19) rồi so sánh các hệ số của 𝑠𝑖𝑛Ω𝑡 và 𝑐𝑜𝑠Ω𝑡, ta rút ra hệ hai phương trình đại số tuyến tính để xác định M và N

0

0

ω2 − Ω2M − 2δΩN = h1 2δΩM + ω2 − Ω2N = h2

Giải ra ta được

0

ω2 − Ω2h1 + 2δΩh2

𝑀 =

0

ω2 − Ω22 + 4𝛿2Ω2

2δΩh1ω2 Ω2h2

N 0

0

ω2 Ω22 42Ω2

(3.21)

Nghiệm tổng quát của phương trình vi phân (3.19) là tổng của nghiệm riêng (3.20) và nghiệm tổng quát của phương trình vi phân thuần nhất (2.28)

q t = Ae−δt sin ωt + β + MsinΩt + NcosΩt (3.22)

Số hạng thứ nhất của biểu thức nghiệm (3.22) biểu diễn thành phần dao động tự do tắt dần. Hai số hạng sau có tần số Ω của ngoại lực biểu diễn thành phần dao động cưỡng bức của hệ.

Thành phần dao động cưỡng bức (3.20) có thể biểu diễn dưới dạng

q∗t = q sin(Ωt + φ) (3.23)

Trong đó

M2  N2

qˆ 

h2  h2

h2  h2

1 2



ω  Ω  4δ Ω

2 2

0



2

2 2

ω

0

1 2

(3.24)

tgφ N

M

21 η22 4D2η2

(3.25)

Ở đây, cũng như các đoạn trước, ta dùng ký hiệu η = Ω

ω0

, D = δ . So sánh

ω0

phương trình vi phân (3.19) với các phương trình vi phân (3.6), (3.7) và (3.8) ta rút ra các hệ thức sau:

- Trường hợp kích động lực hoặc kích động qua lò xo

q = V1η, D y ; V1 = 1 − η2

- Trường hợp kích động động học

2 + 4D2 η2

1

−

2 (3.26)

q = V2η, Dy ; V2 = 1 + 4D2η2 V1 (3.27)

- Trường hợp kích động bởi khối lượng lệch tâm

q = V3η, D y ; V3 = η2V1 (3.28)

Các hàm V1, V2, V3 được gọi là các hàm khuếch đại (hay các hệ số động lực). Đồ thị của các hàm khuếch đại V1, V2, V3 ứng với một vài giá trị của độ cản Lehr D cho trên hình 2.27.

Khi ta cố định độ cản D (xem như đã cho), các hàm V1, V2, V3 đạt cực đại tại các giá trị sau của 𝜂 :

V1 đạt cực đại khi η = 1 − 2D2

2

V đạt cực đại khi η = 1 + 8D2 − 1

2D

3 2

V đạt cực đại khi η = 1

1−2D

≈ 1 − 2D2 nếu D << 1

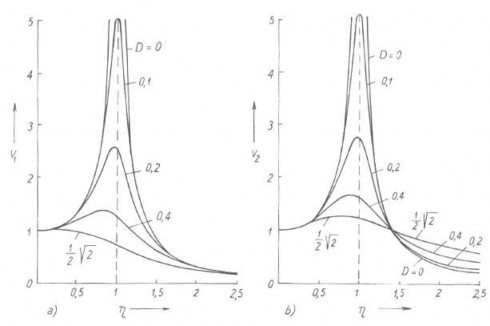
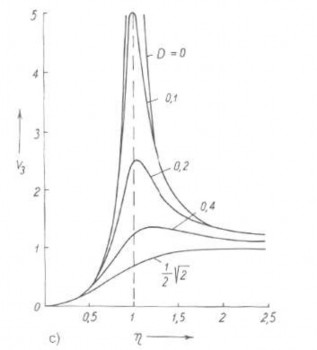
Hình 2.27 Đồ thị các hàm khuyếch đại V1, V2, V3

Ta có thể tính được các giá trị cực đại này

2D 1 D2

max V  max V  1

η 1 η 3

max V

 115D2 

khi D nhỏ

η 2 2D 2 



Góc pha ban đầu 𝜑 được xác định bởi hệ thức (3.25)

2δΩh1ω2 Ω2h2

tgφ 

ω2 Ω2h

0

 2δΩh

0 1 2

Trường hợp kích động lực và kích động bởi khối lượng lệch tâm

−2δΩ

−2Dη

2Dη

tgφ = = → φ = −arctg

0

ω2 − Ω2 1 − η2 1 − η2

Trường hợp kích động động học, ta có

-2δΩ3 -2Dη3

tgφ= ω2-Ω2ω2+4δ2Ω2 = 1-η2+4D2η2

0 0

2Dη3

→φ=-arctg

1-η2+4D2η2

Nếu ta ký hiệu Ψ = −𝜑 thì ta có ba hệ thức sau

Ψ = 0 𝑘𝑕𝑖 𝜂 → 0 : Dao động cùng pha

Ψ = π 2 khi η = 1 : Cộng hưởng

Ψ = π khi η → ∞ : Dao động ngược pha

Trường hợp kích động động lực hoặc kích động bởi khối lượng lệch tâm, sự phụ thuộc của góc Ψ vào 𝜂 ứng với một vài giá trị của D được biểu diễn trên hình 2.28

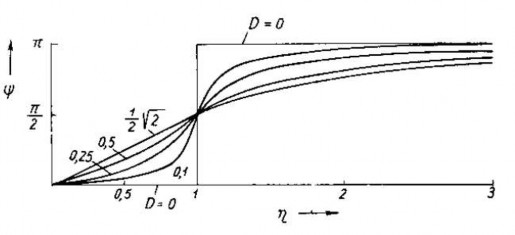
Hình 2.28 Đồ thị biểu diễn sự phụ thuộc của góc 𝛹 vào 𝜂

Để tìm nghiệm của phương trình vi phân mô tả dao động cưỡng bức người ta cũng hay sử dụng phương pháp biên độ phức. Muốn vậy ta đưa vào các ký hiệu sau

y t = y sin Ωt = Imy t ; y t = y eiΩt

x t = x sin Ωt + φ = Imx t ; x t = x ei Ωt+φ

x t = x ei Ωt+φ = x eiφ eiΩt = x eiΩt ; x = x eiφ

Sử dụng cách biểu diễn phức như trên ta có thể tìm được nghiệm các phương trình (3.6), (3.7) và (3.8) dưới dạng phức

Thế y t = y eiΩt cho y sin Ωt và x = x eiΩt cho x(t) trong phương trình (3.6) ta nhận được phương trình

ω2 − Ω2 + i2Dω0Ω 𝑥 = ω2 y (3.29)

0 0

0

iφ ω2

x%xˆe

 ω2  Ω2

0 yˆ

 i2Dω0Ω

Nhân cả tử số và mẫu số hệ thức (3.29) với số phức liên hợp của số phức ở mẫu số và sau một vài phép biến đổi ta được

x%xˆeiφ 

1 η2  i2Dη

2yˆ

(3.30)

1 η2  4D2η2

Tính toán tương tự đối với các phương trình (3.7), (3.8). Từ phương trình (3.8)

ta có

x%= xˆeiφ =

1- η2-i2Dη yˆ

1-η22+ 4D2η2

(3.31)

Từ phương trình (3.7) ta có

x% xˆeiφ 

1 η2  i2Dη

2

η2yˆ

(3.32)

1 η2  4D2η2

Thí dụ 2.13: Sơ đồ một thiết bị đo dao động được biểu diễn trên hình 2.29a. Vỏ ngoài thiết bị đo bị rung theo qui luật xm = x0 cos Ωt. Phải chọn các tham số khối lượng m và độ cứng c như thế nào để với hệ số cản tuỳ ý kim chỉ đúng biên độ kích động x0 trong một dải tần số đo đủ rộng.

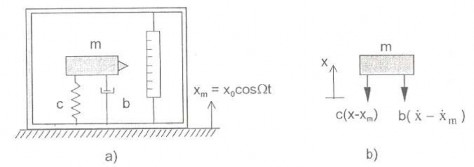
Hình 2.29 Hình thí dụ 2.13

Lời giải: Ta chọn toạ độ x là dịch chuyển của khối lượng m so với nền cố định (hình 2.29b). Dịch chuyển, vận tốc của khối lượng m đối với vỏ ngoài thiết bị là

x − xm , x − x m .

Phương trình vi phân chuyển động của khối lượng m là

động

được

mx = −c x − xm − b x − x m

Kim của thiết bị đo chỉ độ lệch tương đối xr = x – xm . Từ đầu bài ta có

x m = −x0Ω2 cosΩt. Thế vào phương trình trên ta nhận được phương trình dao

mx r + bx r + cxr = mΩ2 x0 cos Ωt

Chia cả hai vế phương trình trên cho m và sử dụng các ký hiệu quen biết ta

0

x r + 2δx r + ω2xr = Ω2x0 cos Ωt

Nghiệm riêng của phương trình trên có dạng

xr = x0V3 cos Ωt − φ

Biên độ đo được và biên độ kích động sẽ trùng nhau khi V3 = 1. Theo hình

2.27c kết quả đo sẽ không phụ thuộc vào độ cản D khi η ≫ 1. Từ đó suy ra

ω2 ≪ Ω2 → c

≪ Ω2

0 m

Như vậy phải chọn c và m sao cho tần số riêng của hệ dao động không cản bé hơn nhiều tần số của kích động.

Thí dụ 2.14: Để xác định độ cản của hệ như hình 2.30, ta lắp vào khối lượng rung hai môtơ lệch tâm. Cho biết 2∆me = 130 kgcm. Khối lượng của hệ là M = 1800 kg, tổng các hệ số cứng của các lò xo là c* = 7200 N/cm. Các mô tơ lệch tâm quay với vận tóc góc Ω = 20s−1. Biên độ dao động

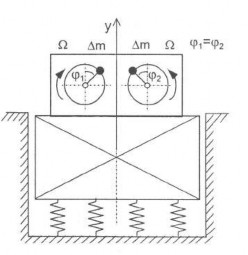
của hệ đo được là y = 0,2cm. Hãy xác định các hệ số cản D, δ, b.

Lời giải: Phương trình vi phân dao động của hệ có dạng

My + by + c∗y = 2∆meΩ2 sin Ωt

Chia hai vế cho M ta được

0

y + 2δy + ω2y = Ω2y0 sin Ωt

với 𝑦0

= 2∆𝑚𝑒 .

𝑀

Nghiệm của phương trình trên có dạng

y t = y sin Ωt + φ

Trong đó 𝑦 = 𝑉3𝜂, 𝐷 𝑦0 = 𝑦0𝜂2𝑉1. Từ đó suy ra

Hình 2.30 Hình thí dụ 2.14

V1 =

1

22

y

=

2 2 y η2

1 − η + 4D η 0

y0η2

→ 1 − η22 + 4D2 η2 =

y

y η

2 4

→ 1 − η22 + 4D2η2 = 0

y 2

Từ công thức cuối ta giải ra 𝐷 = 1

2𝜂

2

𝑦0𝜂4 − 1 − 𝜂22

𝑦

Theo các số liệu ở đầu bài ta có

𝑐∗

𝜔0 =𝑀 =

7200. 102

= 20𝑠−1 = Ω

1800

2Δme 130

y0 =

= = 0,072cm M 1800

2

Vậy ta có D = 10,072− 0 = 0,1806

2 0,2

Từ đó suy ra: δ = Dω0 = 3,611 1 s,

b = 2Mδ = 13000kg/s

Thí dụ 2.15: Bộ phận làm việc của máy đầm đất có khối lượng M tựa trên các lò xo như hình 2.31a. Khối lượng vỏ máy là m. Ở bộ phận làm việc có hai khối lượng lệch tâm (mỗi khối lượng là m2/2) quay với số vòng quay là n. Hãy chọn các tham số của máy sao cho máy làm việc ở vùng cộng hưởng và trong quá trình làm việc vỏ máy không nẩy lên khỏi đất.

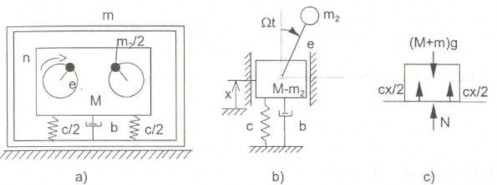
Hình 2.31 Hình thí dụ 2.15

Lời giải: Mô hình cơ học của bộ phận làm việc của máy như hình 2.31b. Bộ phận này dao động quanh vị trí cân bằng tĩnh. Toạ độ của m2 là

x2 = x + e cos Ωt

Phương trình vi phân chuyển động của mô hình máy làm đất là

0

Mx + bx + cx = Ω2 m2e cos Ωt x + 2δx + ω2x = Ω2x0 cos Ωt

với x0 = m2e/M.

Nghiệm của phương trình này theo (3.23) có dạng

x = x0V3 cos Ωt − φ

Xem tất cả 182 trang.