A ω = a ω
c2t2
A2ω = a2ω =0
π2
sinωt0 2
ωt0
Có thể bạn quan tâm!
-
Dao động kỹ thuật - 1 -
Dao động kỹ thuật - 2 -
Biểu Diễn Dao Động Tuần Hoàn Trên Mặt Phẳng Pha -
Xác Định Các Tham Số Độ Cứng Của Hệ Dao Động -
Tính Toán Dao Động Tự Do Có Ma Sát Nhớt -
A Đồ Thị Dao Động Tự Do Có Ma Sát Khô Với Điều Kiện Đầu 𝑡 = 0 ∶
Xem toàn bộ 182 trang tài liệu này.
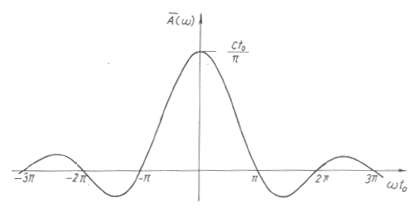
Hình 1.19b Đồ thị hàm 𝐴 𝜔
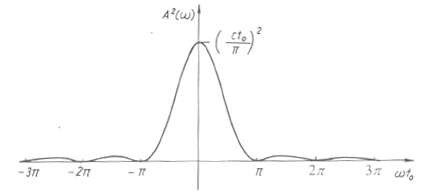
Hình 1.19c Đồ thị hàm 𝐴2 (𝜔)
Trên hình (1.19b) và (1.19c) là đồ thị các hàm A(ω) và A2 (ω).
Biểu diễn tích phân Fourier của hàm y(t) theo công thức (3.6) có dạng
∞
c
y t = a ω cosωtdω =
π
−∞
1.3.3 Dao động họ hình sin
∞
sinωt0cosωt
dω
ω
−∞
Dao động họ hình sin được mô tả về phương diện động học bởi hệ thức
y t = A t sin ω t t + α(t) (3.17)
Trong đó A(t), ω(t) và α(t) là các đại lượng dao động thay đổi chậm theo thời gian. Nếu chỉ có A(t) thay đổi thì dao động được gọi là dao động với biên độ biến đổi. Tương tự ta có dao động với tần số biến đổi khi chỉ có 𝜔(𝑡) thay đổi, dao động với pha biến đổi khi chỉ có 𝛼(𝑡) biến đổi. Dao động với pha biến đổi thì tần số của nó cũng biến đổi, bởi vì tần số của dao động họ hình sin được xác định bởi hệ thức
d
ωa = dt ω t t + α(t) (3.18)
Giả sử ta có dao động mà A t = A0 , ω = ω0 + g t , α = α0 + h(t). Khi đó áp dụng các biến đổi lượng giác ta có
y t = A0sin ω0 t + α0 + g t t + h(t)
= A0 sin ω0t + α0 cos g t t + h(t) + sin g t t + h(t) cos(ω0t + α0)
= A1 t sin ω0t + α0 + A2 t cos(ω0t + α0)
Như thế dao động với tần số hoặc pha biến đổi có thể xem như là tổng hợp của hai dao động với biên độ biến đổi.
Dao động với biên độ biến đổi theo quy luật
A t = A0 eβt
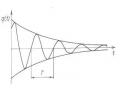
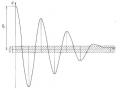
có một vai trò quan trọng trong lý thuyết dao động. Nếu β < 0 thì dao động tắt dần, nếu β > 0 dao động tăng dần. Trên hình 1.20a biểu diễn dao động tắt dần trong miền thời gian, còn hình 1.21 biểu diễn dao động tăng dần trong miền thời gian (β =
+0,046ω). Hình 1.20b biểu diễn dao động tắt dần trên mặt phẳng pha.
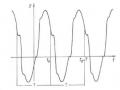
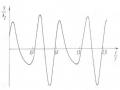
Dao động mà biên độ thay đổi luân phiên được gọi là dao động biến điệu (hình 1.22). Trong các loại dao động tần số thay đổi, người ta phân biệt dao động tần số thay đổi đơn điệu (hình 1.23) và dao động tần số thay đổi biến điệu (hình 1.24). Các dao động biến điệu có một vai trò quan trọng trong kỹ thuật vô tuyến điện.
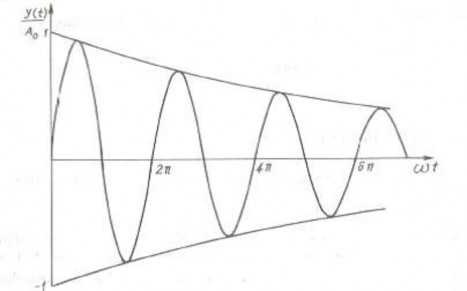
Hình 1.20a Dao động họ hình sin tắt dần
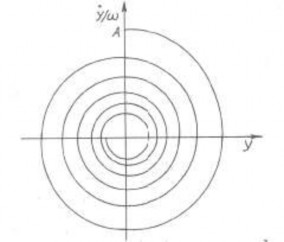
Hình 1.20b Dao động tắt dần trên mặt phẳng pha
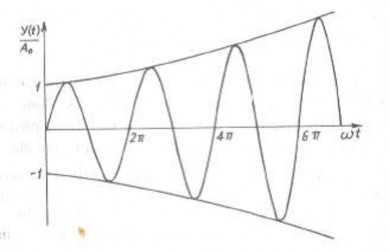
Hình 1.21 Dao động họ hình sin tăng dần
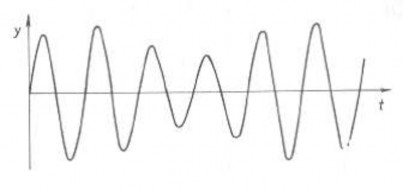
Hình 1.22 Dao động biên độ biến điệu
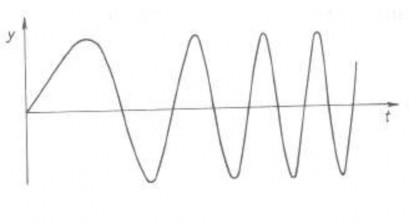
Hình 1.23 Dao động tần số thay đổi đơn điệu
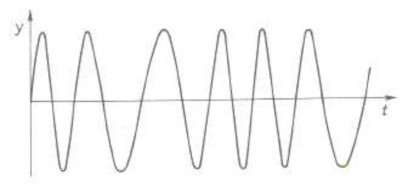
Hình 1.24 Dao động tần số thay đổi biến điệu
CÂU HỎI ÔN TẬP
hoà.
1. Thế nào là dao động điều hoà, nêu các tham số động học của dao động điều
2. Biểu diễn phức dao động điều hoà y(t) = Asin(t + ).
3. Tổng hợp hai dao động điều hoà: y1(t) = A1sin(t + 1) và y2(t) = A2sin(t +
2) theo 2 phương pháp đại số và biểu diễn phức.
4. Thế nào là dao động tuần hoàn, nêu các tham số động học của dao động tuần
hoàn.
5. Tổng hợp hai dao động điều hoà cùng phương khác tần số với tỷ lệ giữa hai
tần số là hữu tỷ.
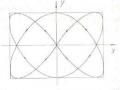
6. Biểu diễn đồng thời hai đại lượng dao động điều hoà theo hai phương vuông góc với nhau.
7. Thế nào là dao động không tuần hoàn.
8. Tổng hợp hai dao động điều hoà cùng phương khác tần số với tỷ lệ giữa hai tần số là số vô tỷ.
9. Thế nào là dao động họ hình sin. Trình bày dạng dao động họ hình sin tắt dần, tăng dần.
10. Tổng hợp hai dao động điều hoà cùng phương với tỷ lệ hai tần số là
1:2=1/2, A1 = A2, 1 = 2 = 0.
Chương 2
DAO ĐỘNG TUYẾN TÍNH CỦA HỆ MỘT BẬC TỰ DO
Hệ cơ học hôlônôm một bậc tự do là cơ hệ mà vị trí của nó trong không gian được xác định bởi một toạ độ suy rộng. Chuyển động của hệ được xác định bởi qui luật thay đổi của toạ độ suy rộng đó theo thời gian.
Trong chương này ta xét dao động nhỏ của hệ một bậc tự do quanh vị trí cân bằng ổn định. Khi đó phương trình vi phân mô tả dao động của hệ sẽ là phương trình vi phân tuyến tính cấp hai hệ số hằng số.
2.1 DAO ĐỘNG TỰ DO KHÔNG CẢN
2.1.1 Các thí dụ về thiết lập phương trình vi phân dao động
Trước hết chúng ta xét một vài thí dụ về thiết lập phương trình vi phân dao động tự do không cản của hệ một bậc tự do.
Thí dụ 2.1: Dao động của một vật nặng treo vào lò xo.
Xét một vật nặng khối lượng m treo vào lò xo có hệ số cứng c. Bỏ qua khối lượng lò xo (hình 2.1)
Động năng và thế năng của hệ có dạng
T = 1
2
mx2
, Π =
1 cx2
2
Thế các biểu thức động năng và thế năng trên vào phương trình Lagrange loại hai
d ∂T ∂T ∂Π
− = −
dt ∂x ∂x ∂x
c
Vị trí cân
x bằng tĩnh
ta nhận được phương trình dao động của hệ
mx + cx = 0 (1.1)
Chú ý rằng ta có thể nhận được phương trình dao động (1.1) bằng nhiều phương pháp khác nhau.
Chẳng hạn, nếu sử dụng định luật Newton ta có
mx = P − c(x0 + x)
m
Hình 2.1 Dao động của vật nặng treo vào lò xo
trong đó x0 là độ dãn tĩnh của lò xo P = cx0, còn biểu thức của lực đàn hồi tuyến tính của lò xo Fđh = c(x0 + x), lực đàn hồi hướng ngược chiều trục x. Từ phương trình trên ta suy ra
mx + cx = 0
Thí dụ 2.2: Dao động con lắc toán học.
Con lắc toán học là một hệ dao động gồm một chất điểm có khối lượng m treo vào một điểm O cố định bằng một sợi dây nhẹ, không dãn chiều dài là l (hình 2.2). Gọi
O
y
l
Q
x
Vị trí cân bằng tĩnh
toạ độ của chất điểm là x, y. Từ hình vẽ ta có 𝑥 = 𝑙𝑠𝑖𝑛𝜑 , 𝑦 = 𝑙𝑐𝑜𝑠𝜑. Từ đó dễ dàng tính được các biểu thức động năng của chất điểm
1 1
T = m x2 + y2= ml2 φ 2
2 2
Π = −mgy = −mglcosφ
Thế các biểu thức trên vào phương trình Lagrange loại hai lực ta được
ml2φ = −mglsinφ
Hay
φ +
g sinφ = 0
l P
Trong trường hợp con lắc dao động nhỏ, ta có thể lấy xấp xỉ sinφ ≈ φ. Khi đó phương trình dao động nhỏ của con lắc toán học có dạng
g
Hình 2.2 Dao động con lắc toán học
φ +
φ = 0 (1.2)
l
O
C
mg
Thí dụ 2.3: Dao động con lắc vật lý.
a
Con lắc vật lý là một hệ dao động gồm có một vật rắn có thể quay quanh một trục cố định đi qua O và vuông góc với mặt phẳng chứa khối tâm C của vật (hình 2.3). Khoảng cách từ điểm O đến khối tâm C của vật là a, mômen quán tính của vật rắn với trục quay là J0. Biểu thức động năng và thế năng của hệ có dạng
1
T = J
φ 2 , Π = −mgacosφ
Vị trí cân
2 0 bằng tĩnh
Thế các biểu thức động năng và thế năng vào phương trình Lagrange loại hai ta được
J0φ + mgasinφ = 0
Hình 2.3 Dao động con lắc vật lý
Trong trường hợp con lắc vật lý dao động nhỏ, ta lấy sinφ ≈ φ, phương trình vi phân dao động có dạng
J0φ + mgaφ = 0 (1.3)
Thí dụ 2.4: Dao động xoắn.
Xét dao động xoắn của một vật nặng (chẳng hạn một đĩa hình tròn) gắn chặt vào một trục đàn hồi. Đầu kia của trục đàn hồi ngàm chặt vào tường cố định (hình 2.4). Cho biết mômen quán tính của vật nặng đối với trục quay là J, độ cứng xoắn của trục đàn hồi là c.
c
J Vòtrí
caân baèng tónh
Hình 2.4 Dao động xoắn
Giả thiết mômen quán tính của trục đàn hồi đối với trục quay nhỏ hơn nhiều so với mômen quán tính của vật nặng đối với trục quay. Biểu thức động năng và thế năng của hệ có dạng
1 1
T = Jφ 2 , Π = cφ2
2 2
Thế các biểu thức động năng và thế năng vào phương trình Lagrange loại hai ta nhận được phương trình dao động xoắn tuyến tính của vật nặng
Jφ + cφ = 0 (1.4)
Gọi q là toạ độ suy rộng. Từ các phương trình (1.1), (1.2), (1.3), (1.4) ta thấy dạng của phương trình dao động tự do không cản của hệ một bậc tự do có dạng chung là
mq + cq = 0 (1.5)
2.1.2 Tính toán dao động tự do không cản
Nếu ta sử dụng ký hiệu
0
ω2 c
m
(1.6)
Thì phương trình dao động tự do không cản có dạng
0
q + ω2 q = 0 (1.7)
Như đã biết từ lý thuyết phương trình vi phân, nghiệm của phương trình vi phân (1.7) có dạng như sau
q = C1cosω0t + C2sinω0 t (1.8)
Trong đó C1, C2 là hằng số tuỳ ý. Các hằng số này được xác định từ các điều kiện đầu
t = 0: q 0 = q0 , q 0 = q 0
Để xác định các hằng số C1 , C2 ta đạo hàm biểu thức (1.8) theo thời gian
q = −C1ω0sinω0t + C2ω0cosω0t (1.9)
Thế các điều kiện đầu vào các biểu thức (1.8) và (1.9) ta xác định được
q0
ω
C1 = q0 , C2 =
0
(1.10)
Chú ý rằng nghiệm (1.8) của phương trình vi phân (1.7) có thể viết dưới dạng
q = Asin ω0t + α (1.11)
Trong đó A và 𝛼 là các hằng số tuỳ ý. Do hệ thức
sin ω0 t + α = sinω0 tcosα + sinαcosω0t
nên từ (1.8), (1.10) và (1.11) dễ dàng tính được
2 2 2
q0 2
C1 q0
A = C1 + C2 = q0 +
ω
0
, tgα =
C2
= ω0
q
0
(1.12)