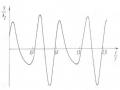
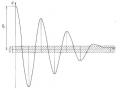
Từ biểu thức (1.11) ta thấy dao động tự do không cản của hệ một bậc tự do được mô tả bởi hàm điều hoà. Vì vậy dao động tự do không cản còn được gọi là dao động điều hoà.
Theo chương 1, trong biểu thức (1.11), A được gọi là biên độ dao động, ω0 được gọi là tần số riêng, ω0t + α được gọi là pha dao động, α là pha ban đầu. Đại lượng T = 2π ω0 được gọi là chu kỳ dao động.
Qua khảo sát trên, dao động tự do không cản của hệ một bậc tự do là dao động điều hoà và có các tính chất sau:
- Tần số riêng và chu kỳ dao động không phụ thuộc vào các điều kiện đầu mà chỉ phụ thuộc vào các tham số của hệ.
- Biên độ dao động là hằng số. Biên độ dao động và pha ban đầu của dao động tự do không cản phụ thuộc vào các điều kiện đầu và các tham số của hệ.
Việc xác định tần số dao động riêng theo công thức (1.6) là nhiệm vụ quan trọng nhất của bài toán dao động tự do. Bảng 2.1 thống kê một số công thức tính tần số riêng của một số hệ dao động đơn giản.
Thí dụ 2.5: Tay biên khối lượng m, dài l. Tìm toạ độ trọng tâm và mômen quán tính của tay biên đối với trục qua trọng tâm và vuông góc với mặt phẳng tay biên. Các kích thước cho trên hình vẽ.
B
m
b
C
l
a
A
Hình 2.5 Tay biên
Lời giải: Ta sẽ xác định các đại lượng trên bằng thực nghiệm (hình 2.5). Gọi vị trí trọng tâm là C. Các khoảng cách a, b trên hình là các đại lượng cần tìm, với a = l –
b. Ký hiệu JA, JB là mômen quán tính của tay biên lần lượt đối với các trục đi qua A, B và vuông góc với mặt phẳng hình vẽ. JA, JB là các đại lượng chưa biết. Ta làm hai thí nghiệm xem tay biên là con lắc vật lý, lần lượt có các điểm treo là A rồi B.
Phương trình dao động nhỏ quanh A, theo (1.3) là
JA φ A + mgaφA = 0
Từ đó suy ra chu kỳ dao động quanh A
T 2π 2π
JA
mga
A ω
(1.13)
A
Tương tự, phương trình dao động nhỏ của tay biên quanh B là
JB φ B + mgbφB = 0
Từ đó suy ra chu kỳ dao động
T 2π 2π
JB
mgb
B ω
(1.14)
B
Các đại lượng TA, TB ở trên được xác định bằng thực nghiệm (chẳng hạn sử dụng đồng hồ bấm giây). Ngoài ra, ta còn có ba phương trình
a + b = l , JA = JC + ma2 , JB = JC + mb2 (1.15)
Như thế ta có năm phương trình để xác định năm ẩn là JA , JB , JC , a, b. Giải các phương trình trên ta được
b l
gT2 4π2l
A
A
B
g T2 T2 8π2l
Jc Bmgb mb
T2 2
4π2
0
Số TT Mô hình dao động Phương trình 𝜔2
X
c
1 Hệ khối lượng – lò xo đơn giản m
c c
x + x = 0
m m
Hệ khối lượng – lò xo trong c
2 y
trọng trường m
y +
c c
y = 0
m m
O
l
3 Con lắc toán học φ +
g g
φ = 0
l l
m
O rc
mgrC
mgrC g
4 Con lắc vật lý φ + J
C0
m
φ = 0
=
J0 Jred
Jo
cd cd
5 Bàn quay φ + J
φ = 0
J
Cd 0 0
Hệ khối lượng vắt qua ròng rọc | C | r m1 | Jo y | l c y + J0 m y = 0 l + m r2l l | l c l + J0 ml ml r2 | |
7 | Cơ cấu gò nhịp | m | O Cd | cd − mgl φ + φ = 0 J0 | cd − mgl J0 | |
8 | Hệ con lăn – lò xo | c | X | Jc C r | l c x + JC m x = 0 l + mr2 | l c l + JC m mr2 |
9 | Con lăn trên quỹ đạo tròn | | Jc r C | l g ψ+ J l ψ = 0 l + C2 mr | l g l + JC l mr2 | |
10 | Nửa đĩa tròn trên mặt phẳng | rc m C r | mgrC φ + φ = 0 JC + m r − rC2 | mgrC JC + m r − rC2 | ||
Có thể bạn quan tâm!
-
Dao động kỹ thuật - 2 -
Biểu Diễn Dao Động Tuần Hoàn Trên Mặt Phẳng Pha -
Các Thí Dụ Về Thiết Lập Phương Trình Vi Phân Dao Động -
Tính Toán Dao Động Tự Do Có Ma Sát Nhớt -
A Đồ Thị Dao Động Tự Do Có Ma Sát Khô Với Điều Kiện Đầu 𝑡 = 0 ∶ -
Đồ Thị Biểu Diễn Sự Phụ Thuộc Của Góc 𝛹 Vào 𝜂
Xem toàn bộ 182 trang tài liệu này.
l
l
O
Bảng 2.1. Tần số riêng của một vài mô hình dao động
2.1.3 Xác định các tham số độ cứng của hệ dao động
Các phần tử đàn hồi trong các hệ dao động hữu hạn bậc tự do thường được giả thiết bỏ qua khối lượng. Đại lượng đặc trưng cho phần tử đàn hồi tuyến tính có độ cứng và ký hiệu là c. Vì hệ có thể thực hiện được dao động thẳng, dao động uốn, dao động xoắn… nên thứ nguyên của độ cứng c nói chung khác nhau. Phần tử đàn hồi có nhiều dạng và nhiều kết cấu tuỳ theo sự sử dụng và cách chịu lực của chúng. Dưới đây trình bày một số công thức tính toán hệ số cứng c qui đổi.
a. Tính toán hệ số cứng qui đổi của thanh đàn hồi
l
l
F
Nếu lò xo là các thanh đàn hồi không trọng lượng, ta có thể tính toán hệ số cứng quy đổi tương đối đơn giản. Trong trường hợp thanh đàn hồi (lò xo) chịu kéo nén (hình 2.6), từ giáo trình Sức bền vật liệu [37, 49] ta có
Fl
Δl =
EA
Trong đó E là mô đun đàn hồi, A là diện tích mặt cắt ngang. Từ đó ta suy ra
EA
F = Δl = cΔl l
Vậy độ cứng qui đổi được xác định bởi công thức
EA
c = (1.16)
l
Trong trường hợp thanh đàn hồi (lò xo) chịu xoắn
(hình 2.7) từ giáo trình Sức bền vật liệu ta có công thức
Δφ =
Mx l
Hình 2.6 Thanh đàn hồi
chịu kéo
GIp
Trong đó G là mô đun trượt, Ip là mômen quán tính cực của mặt cắt ngang. Từ công thức trên dễ dàng suy ra
Mx
l
GIp
Mx = ∆φ = c∆φ l
Vậy độ cứng qui đổi trong trường hợp thanh xoắn có dạng
GIp
c =
l
(1.17)
Trường hợp thanh đàn hồi (lò xo) bị uốn, hệ số cứng qui đổi c còn phụ thuộc vào các điều kiện biên. Để làm thí dụ ta xét dầm chịu uốn như hình 2.8. Từ giáo trình Sức bền vật liệu, ta tính được độ vòng f [37, 49]
l Fl3
f =
3 EI
Hình 2.7 Thanh đàn hồi chịu xoắn
l
Trong đó EI là độ cứng chống uốn.
Từ đó suy ra F
3EI
F = l3 f = cf
Vậy độ cứng qui đổi c được xác định bởi công thức
f
Hình 2.8 Dầm chịu uốn
c 3 EI
l3
(1.18)
b. Tính toán lò xo thay thế tương đương của các hệ các lò xo mắc song song và mắc nối tiếp
Đối với hệ có hai lò xo mắc song song như hình 2.9, ta có thể thay thế tương đương bằng hệ có một lò xo. Từ biểu thức lực đàn hồi lò xo, ta suy ra công thức tính hệ số cứng lò xo tương đương
F = c1x + c2x = c∗x → c∗ = c1 + c2
c2
x
c*
c1
c2
c*
x
c1
Hình 2.9 Hai lò xo mắc song song Hình 2.10 Hai lò xo mắc nối tiếp
Nếu hệ có n lò xo mắc song song, tính toán tương tự ta có
n
j
c* c
(1.19)
jl
Đối với hệ có hai lò xo mắc nối tiếp như hình 2.10, nếu ở hệ thay thế lò xo dãn ra một đoạn x bằng tổng hai độ dãn x1 và x2 của hệ ban đầu thì ta có
F = c1x1 = c2x2 , x1 + x2 = x , F = c∗x
Từ đó ta suy ra
1
2
F F F 1 1 1
x = + = → c1 c2 c∗
c∗ = c + c
Nếu hệ có n lò xo mắc nối tiếp thì công thức tính hệ số cứng lò xo thay thế có
dạng
1 n 1
(1.20)
c
*
c il j
Thí dụ 2.6: Cho hệ dao động gồm khối lượng và các lò xo mắc như hình 2.11.
Hãy tính tần số riêng của hệ.
C1
y
C2
m
C3
C 4
Hình 2.11 Hình thí dụ 2.6
Lời giải: Ở đây ta có bốn lò xo mắc song song. Do đó
∗ c∗
c = c1 + c2 + c3 + c4 , ω0 =m
Thí dụ 2.7: Cho hai hệ dao động như hình 2.12. Mỗi hệ gồm một dầm không trọng lượng có độ cứng chống uốn là EI, một lò xo có độ cứng c và một khối lượng m. Hãy tính các tần số riêng của chúng.
Lời giải: Cả hai hệ đã cho đều có thể thay bằng một mô hình thay thể tương đương (hình 2.12c)
c
EI
m
l/2 l/2
EI c*
m
c
l/2 l/2
m
a) b) c)
Hình 2.12 Hình thí dụ 2.7
Trên hình 2.12a dầm và lò xo là hai lò xo mắc song song. Lò xo thay thế dầm (xem bảng 2.2) có độ cứng quy đổi là
c1 =
48EI
l3
Từ đó dễ dàng tính được lò xo thay thế tương đương của hệ
c∗ = c + c1
48EI
= c +
l3
Tần số riêng của hệ trên hình 2.12a là
c∗
ω0 =m =
cl3 + 48EI ml3
Trên hình 2.12b, dầm và lò xo là hai lò xo mắc nối tiếp. Do đó
1 1 1
= +
cc1
→ c∗ =
c∗ c c1
Tần số riêng của hệ là
c + c1
c∗ 48cEI
ω0 =m = cl3 + 48EI m
Như thế tần số riêng của hệ b nhỏ hơn tần số riêng của hệ a. Nói cách khác, hệ b có lò xo thay thế mềm hơn.
Cuối cùng ta thống kê ra một số công thức hay dùng để tính toán các hệ số cứng của lò xo thay thế trong bảng 2.2.
Thí dụ 2.8: Một khung hình chữ nhật gồm một thanh ngang cứng và hai thanh chống đàn hồi (h = 3m, E = 2,1.105 N/mm2 , I = 3500cm4) như hình 2.13. Trên thanh ngang gắn chặt một vật rắn có khối lượng m = 105kg. Bỏ qua khối lượng các thanh của khung. Xác định tần số riêng của hệ.
EI
h
m
a) b)
A
w
w
c*
m
M
F F
EI
c) d) e)
Hình 2.13 Hình thí dụ 2.8
Lời giải: Khung có khả năng dao động ngang như hình 2.13b, mô hình thay thế tương đương là hình 2.13c. Để tính c* ta phải tính các lò xo tương đương của các thanh chống đàn hồi.