Điều Kiện Cân Bằng Của Hệ Lực Phẳng Song Song

Ry = ∑Fy

Mà mà (∑Fx)2 và (∑Fy)2 là những số dương nên R’ = 0 chỉ khi ∑Fx = 0 và ∑Fy = 0

o o F 

mà M = m nên M = 0 khi

o



*Dạng 2: Điều kiện cần và đủ để một hệ phẳng bất kỳ cân bằng là tổng đại số mô men của các lực đối với hai điểm bất kỳ trên mặt phẳng và tổng hình chiếu các lực lên trục x không vuông gốc với đường thẳng đi qua hai điểm bất kỳ đó đều bằng không

Có thể bạn quan tâm!

• Cơ kỹ thuật Nghề Công nghệ ô tô - Trường CĐ Lào Cai - 1
• Cơ kỹ thuật Nghề Công nghệ ô tô - Trường CĐ Lào Cai - 2
• Thu Gọn Hệ Lực Phẳng Bất Kỳ Về Một Tâm Cho Trước.
• Chuyển Động Quay Của Vật Rắn Quanh Một Trục Cố Định
• Chuyển Động Của Điểm Thuộc Vật Quay Quanh Một Trục Cố Định
• Cơ kỹ thuật Nghề Công nghệ ô tô - Trường CĐ Lào Cai - 7

Xem toàn bộ 91 trang tài liệu này.

x không vuông góc với AB

Thật vậy và thỏa mãn mô men chính Mo= 0, mặt khác hệ có hợp lực thì phải nằm trên phương AB, nhưng trục x không vuông góc với AB nên ∑Fx= 0 thì R = 0 hệ lực cân bằng.

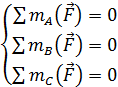
*Dạng 3: Điều kiện cần và đủ để một hệ phẳng bất kỳ cân bằng là tổng đại số mô men của các lực đối với ba điểm không thẳng hàng trên mặt phẳng đều bằng không

A, B, C không thẳng hàng

Thật vậy hệ có hợp lực thì hợp lực đều phải đi qua 3 điểm A, B, C không thẳng hàng điều này không thể xảy ra vì vậy R = 0 hệ lực cân bằng.

Ví dụ:

Thanh AB dài 4 (m), đầu A tựa trên mặt đất, đầu B tựa trên tường cao tại điểm D và lập với tường một góc 

= 30o như hình vẽ. Thanh được cân bằng nhờ sợi dây kim loại AE nằm trên mặt đất.

Xác định phản lực tác dụng lên thanh tại các điểm A và D, sức căng T của dây. Biết trọng lượng thanh P = 200 (N) và đặt tại điểm C chính giữa thanh, chiều cao của tường h = 3 (m).

y

B NC

D



C

h

P NC

T

E A x

Bài giải:

Biên soạn: Tạ Thị Hoàng Thân

Khoa Cơ khí – Động lực Trường Cao đẳng Lào Cai 25



Thanh cân bằng dưới tác dụng của hệ lực ( P, NA , ND , T ) trong đó trọng lực



P đã cho,

D.



T là sức căng của dây AE,



N A và



N D là các phản lực tại các điểm A và

Áp dụng điều kiện cân bằng của hệ lực phẳng, ta có:

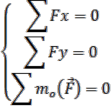- T + ND . cos 30o = 0 (1)

- P + NA + ND . sin 30o = 0 (2)

P . 4 . cos 60o - ND .

2

3 = 0 (3)

cos30o

4 o o

Từ (3) ta có: N

.3= P .

4. cos 60o N

P. .cos60 .cos30

= 2

D D

cos30o 2 3

3

3

200. 4 . 1 .

ND =

2 2 2

3

= 100.

2

= 57,7 (N) thay vào (1) ta có:

T = ND . cos 30o = 100 .

3 . 3 = 50 (N) thay ND = 100.

2 2

3 vào (2) ta có:

2

NA = P - ND . sin 30o = 200 - 100.

3 . 1 = 175 (N)

2 2

Vậy, phản lực tác dụng lên thanh tại các điểm A và D là: NA = 175 (N)

ND = 57,7 (N)

Sức căng T của dây kim loại là: T = 50 (N)

P1

P2

R

4.3. Điều kiện cân bằng của hệ lực phẳng song song 4.3.1 Hợp hai lực phẳng song song cùng

chiều

Hợp của hai lực song song cùng chiều

A C B

là một lực song song cùng chiều với chúng, có trị số bằng tổng các trị số của chúng, còn điểm đặt chia trong đường nối, điểm đặt của hai lực thành hai đoạn tỉ lệ nghịch với trị số của hai lực ấy.

CA  CB  AB

Hình 1.26

A D B

*Ví dụ:

P2 P1 R

Biên soạn: Tạ Thị Hoàng Thân

P

P2

1

Khoa Cơ khí – Động lực Trường Cao đẳng Lào Cai

R

26

P1

P2

A D B

Hình 1.27

Ở hai đầu thanh AB = 0.6 (m), người ta treo những tải trọng P1 = 60 kN và P2 = 20 kN.

Xác định khoảng cách từ A đến D để thanh nằm ngang. Giải:



P 2 .

Muốn thanh AB nằm ngang thì D chính là điểm đặt của hợp lực

R = P1 + P2 = 60 + 20 = 80 (kN)



R của



P1 và

Theo định lý ta có:

AD AB  AD P2 AB 20 .0,6  0,15

(m)

P2 R

R 80

Vậy với khoảng cách AD = 0,15 (m) thì thanh nằm ngang.

4.3.2 Hợp của hai lực song song ngược chiều

Hợp của hai lực song song ngược chiều P2

(không cùng trị số) là một lực song song cùng

chiều với lực có trị số lớn, có giá trị bằng hiệu C

của hai lực đã cho, có điểm đặt chia ngoài đường

nối điểm đặt của hai lực đã cho thành hai đoạn tỉ R

lệ nghịch với trị số của hai lực ấy.

AC  AB  CB

A B

P1

Hình 1.28

*. Ví dụ:



P2 R P1

A

P1

P2



Cho hai lực

P1 và P 2

có P1 = 60 kN và P2 = 20 kN

với AB = 0.4 (m). Xác định hợp lực của hai lực ấy. B

Giải:

Theo định lý hợp hai lực song song ngược chiều ta có: P2

R = P1 - P2 = 60 - 40 = 20 (kN)

B

A

D

R

P1

AD AB  AD P2 .AB 40 .0,4  0,8(m)

Hình 1.29

P2 R

R 20



1Vậy hợp lực của hai lực

P1 và P 2

là:

Hình 1.30

R = 20 (kN) và đặt tại AD = 0,8 (m).

4.3.3. Điều kiện cân bằng của hệ lực phẳng song song

Hệ lực phẳng song song là một trường hợp đặc biệt của hệ lực phẳng ( có đường tác dụng song song và nằm trong một mặt phẳng) nên từ điều kiện cân bằng của hệ lực phẳng có thể suy ra điều kiện cân bằng của hệ lực phẳng song song.

F2

F1

Fn

Giả sử hệ lực phảng song song y



(( F1 , F2 , F3 ,...,Fn ). Chọn hệ trục tọ độ Oxy có trục Oy song song với các lực khi đó hiển nhiên ∑Fx = 0 nên các dạng phương trình cân bằng của hệ lực phẳng song song sẽ là

O x

*Dạng 1: Điều kiện cần và đủ để một hệ phẳng song song cân bằng là tổng hình chiếu của các lực nên trục tọa độ song song với chúng và tổng đại số mô men của các lực đối với một điểm bất kỳ trên mặt phẳng đều bằng không.

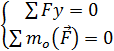
*Dạng 2: Điều kiện cần và đủ để một hệ phẳng song song cân bằng là tổng đại số mô men của các lực đối với hai điểm bất kỳ trên mặt phẳng tác dụng đều bằng không đường thẳng đi qua hai điểm bất kỳ không song song với phương các lực

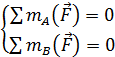
y

YA

C

YB

A

P

1m

1m

B

5m

Ví dụ: Cần trục trọng lượng Q

P = 40kN mang vật nặng Q = 10kN (như hình vẽ). Xác định phản lực từ đường lên hai bánh xe.

Giải: - Khảo sát sự cân bằng của cần trục, cần trục chịu tác dụng của hệ lực song song gồm: - Các tải trọng P, Q

- Các phản lực YA; YB

- Vì cần trục cân bằng nên ta có hệ lực phẳng song song cân bằng

(P, Q, YA; YB ) R 0

- Chọn trục Ay song song với các lực và lập hệ phương trình cân bằng dạng 1: ∑Fy = YA + YB –P –Q = 0 (1)

= 2.YB - 1.P – 5.Q = 0 (2)

Từ (2) suy ra

Từ (1) ta có YA = P + Q - YB = 40 + 10 - 45 = 5kN

CÂU HỎI – BÀI TẬP

1. Lực là gì ? Cách biểu diễn lực.

2. Thế nào là hệ lực, hệ lực cân bằng, hệ lực tương đương.

3. Thế nào là liên kết, phản lực liên kết. Có mấy liên kết cơ bản ? Nêu cách xác định phản lực liên kết của những liên kết đó.

4. Thế nào là giải phóng liên kết ? Khi giải phóng liên kết ta phải làm những gì ?

4. Trình bày qui tắc đa giác lực và điều kiện cân bằng qui tắc đa giác lực.

5. Mômen của hệ lực đối với một điểm là gì? Viết biểu thức tính mômen và cho biết qui ước về dấu.

6. Ngẫu lực là gì? Nêu các tính chất và cách biểu diễn ngẫu lực trong mặt phẳng.

7. Em hãy quan sát mô hình các dạng chịu lực ở hình 1, 2, 3 và đưa ra nhận xét? a.Các trường hợp trên thuộc các dạng liên kết nào đã học?

b.Hãy phân tích lực tác dụng lên vật khảo sát?

H ình 1

H ình 2

H ình 3

8. Trình bày qui tắc đa giác lực và điều kiện cân bằng qui tắc đa giác lực.

9. Phát biểu và viết phương trình cân bằng của hệ lực phẳng bất kỳ?

10. Phát biểu định lý về hợp của hai lực song song cùng chiều và ngược chiều.

11. Phát biểu và viết phương trình cân bằng của hệ lực phẳng song song?

12. Cho hai lực



F1 và F2

đồng qui tại O với F1 = F2,

 = 120o( Hình vẽ ).



Hỏi phải đặt vào điểm O một lực F3

như thế nào để O





hệ lực ( F1 , F2 , F3 ) cân bằng.

13. Một quả bóng bay có trọng lượng P = 20 (N), chịu lực đẩy của không khí lên phía trên là 50 (N) và lực thổi của gió theo phương nằm ngang là 40 (N). Tìm hợp lực ?

14. Ống trụ đồng chất có khối lượng m = 10 (kg) đặt trên giá đỡ ABC hoàn toàn trên và vuông góc ở B. Mặt BC của giá đỡ làm với mặt phẳng nằm ngang 1 góc 45o (Hình vẽ

C

O

A

). Xác định phản lực của giá đỡ lên ống trụ tại hai điểm tiếp xúc D và E.

E

D

B

A

C

B

60

o

30

o

15. Giá ABC dùng để treo vật nặng có khối lượng m = 200 (kg), các góc cho trên hình vẽ. Xác định các phản lực của thanh AC và BC.

16. Bóng đèn có trọng lực P = 50N được treo như hình vẽ. Thanh OA nằm ngang , dây OB hợp với phương của trần một góc α=60o. Hãy xác định hệ lực tác dụng lên nút O?

17. Dầm CD đặt trên hai gối đỡ A và B. Dầm chịu tác dụng của ngẫu lực có mômen m = 8 kN.m, các lực có trị số Q = 20 kN và lực phân bố đều q = 20 kN/m. Xác

định phản lực tại các gối đỡ biết a = 0,8 m. ĐS: NB = 21 kN; YA = 15 kN.

18. Thanh AB dài l = 8m, nặng 12 kg bắt bản lề cố định tại A và tỳ lên tường C cao h = 3m (hình 3.13). Đầu B treo một vật có khối lượng M = 20 kg. Xác định phản lực tại các gối đỡ A và chỗ tỳ C.

ĐS: XA = 260N; YA = 170N; NC = 300N.

CHƯƠNG 2: ĐỘNG HỌC

Mục tiêu:

- Giải thích được các loại chuyển động, các phương trình biểu diễn chuyển động thẳng của chất điểm, vận tốc và gia tốc của chuyển động thẳng, các phương trình biểu diễn chuyển động cong của chất điểm, vận tốc và gia tốc của chuyển động cong.

- Trình bày được các khái niệm và các phương trình biểu diễn chuyển động cơ bản, chuyển động quay quanh một trục cố định, chuyển động tổng hợp, chuyển động song phẳng của vật rắn.

- Xác định được vận tốc, gia tốc của vật rắn chuyển động.

- Rèn luyện tính kỷ luật, kiên trì, cẩn thận, nghiêm túc, chủ động và tích cực sáng tạo trong học tập.

1. CHUYỂN ĐỘNG CƠ BẢN CỦA CHẤT ĐIỂM

1.1 Chuyển động cơ học

1.1.1. Định nghĩa

Sự thay đổi vị trí tương đối của một vật so với các vật khác gọi là chuyển động cơ học.

1.1.2. Tính chất tương đối của một vật

Khi nói vật khác chuyển động bao giờ cũng so sánh nó với vật khác được coi là đứng yên ( gọi là mốc hay tổng quát hơn là hệ quy chiếu ).

Kết luận: Mọi chuyển động và mọi trạng thái nghỉ đều là tương đối.

1.1.3. Quỹ đạo chuyển động

Ta có thể tượng trưng một vật chuyển động bằng một điểm. Quỹ đạo là đường do điểm vạch ra trong quá trình chuyển động.

Tuỳ theo quỹ đạo là đường thẳng hay đường cong mà ta có chuyển động thẳng hay chuyển động cong.

1.2 Chuyển động thẳng đều

1.2.1. Định nghĩa

Chuyển động đều là chuyển động mà vật đi được những quãng đường bằng nhau trong những khoảng thời gian như nhau.

Quỹ đạo là đường thẳng ta có chuyển động thẳng đều.

1.2.2. Vận tốc

a. Khái niệm: Vận tốc là đại lượng đặc trưng cho sự nhanh hay chậm của chuyển động.

b. Đơn vị:

Ký hiệu v =

S(m); (km)

t(s); (h)

= v (m/s); (km/h)