mo( F1 ) = F1.Oa
mo( F2 ) = F2.Ob
mo( R ) = R.Oc
Trong đó:
R = F1 + F2 ; Oc = Ob + bc ; Vì thế: mo( R ) = (F1 + F2).(Ob + bc)
= F1.Ob + F1bc + F2.Ob + F2.bc
Có thể bạn quan tâm!
-
Cơ kỹ thuật Nghề Công nghệ ô tô - Trường CĐ Lào Cai - 1 -
Cơ kỹ thuật Nghề Công nghệ ô tô - Trường CĐ Lào Cai - 2 -
Điều Kiện Cân Bằng Của Hệ Lực Phẳng Song Song -
Chuyển Động Quay Của Vật Rắn Quanh Một Trục Cố Định -
Chuyển Động Của Điểm Thuộc Vật Quay Quanh Một Trục Cố Định
Xem toàn bộ 91 trang tài liệu này.
Nhưng
F1 BC bc
hay F1.ca = F2.bc
F2 AC ca
Nên mo( R ) = F1.Ob + F1bc + F1.ca + F2.Ob
= F1.(Ob + bc + ca) + F2.Ob = F1.Oa + F2.Ob
Suy ra: mo( R ) = mo( F1 ) + mo( F2 )
c. Trường hợp hệ gồm nhiều hệ lực phẳng bất kỳ:
Giả sử hệ gồm n lực bất kỳ ( F1 , F2 , F3 ,...,Fn ), O là điểm nào đó nằm trên mặt phẳng chứa các lực.
Ta phải chứng minh: mo( R ) = mo( F1 ) + mo( F2 ) + ... + mo( F n )
Thật vây, bằng cách xét từng đôi lực, đầu tiên ta xét hai lựcF1 , F2 có hợp
lực R 1 . Hai lực này hoặc đồng qui hoặc song song nên theo cách chứng minh trên
ta có:
mo( R 1 ) = mo( F1 ) + mo( F2 )
Tiếp tục xét hai lực R 1
và F3
có hợp lực
R 2 :
mo( R 2 ) = mo( R1 ) + mo( F3 ) = mo( F1 ) + mo( F2 ) + mo( F3 )
lực là
Tiếp tục xét lần lượt như thế cho đến lực cuối cùng
R ta sẽ có điều cần phải chứng minh.
F n , có hợp lực của hệ
3.2 Ngẫu lực
3.2.1 Khái niệm
Định nghĩa: Hệ lực gồm hai lực song song trái chiều cùng trị số gọi là một ngẫu lực.
F1
F2
F1
Hình 1.34
M
Ngẫu lực có các tính chất sau:
+ Ngẫu lực không làm cho vật cân bằng
+ Ngẫu lực không tương đương với một lực
+ Ngẫu lực không có xu hướng làm cho vật chuyển động quay
Từ ba nhận xét trên ta thấy để xác định được một ngẫu lực ta cần có các yếu
tố
+ Mặt phẳng tác dụng của ngẫu lực là mặt phẳng chứa các lực
+ Chiều quay của ngẫu lực là chiều quay vòng theo chiều tác dụng của các
lực với quy ước: chiều dương là chiều ngược chiều kim đồng hồ, còn chiều âm là chiều quay thuận với chiều kim đồng hồ
+ Trị số mômen của ngẫu lực : là đại lượng xác định bởi tích số
M = F. d
lực
Trong đó:
F là trị số của các lực
d là khoảng cách giữa hai lực, còn gọi là cách tay đòn của ngẫu. M là đại lượng vô hướng có đơn vị là N.m
Ta thấy các yếu tố xác định ngẫu lực gần tương tự như các yếu tố xác định
Vậy có thể nói ngẫu lực cũng là dạng tối giản của hệ lực phẳng. Người ta cũng có thể biểu diễn ngẫu lực bằng một vectơ sao cho
+ Phương của vectơ ngẫu lực vuông góc với mặt phẳng tác dụng của ngẫu
+ Hướng của vectơ sao cho nhìn từ ngọn vectơ xuống mặt phẳng tác dụng
ngẫu lực có xu hướng quay theo chiều kim đồng hồ.
+ Độ dài của vectơ biểu diễn trị số của momen ngẫu lực.
3.2.2 Các định lý về ngẫu lực
Định lý 1: Hai ngẫu lực nằm trong cùng một mặt phẳng, có cùng chiều quay và trị số momen tương đương với nhau.
F4
F3
F2
C
F1
F1
F2
F2
F3
A
F4
F1
F1
Hình 1.35
Chứng minh: giả sử có hai ngẫu lực (F1, F1’) và (F2, F2’) tác dụng trên cùng một mặt phẳng tương đương với nhau, đường tác dụng của chúng cắt nhau tại A, B,C ,D
Trượt lực F1 về A, F1’ về C
Phân tích các lực F1, F1’ thành các lực F3, F4 và F3’, F4’ sao cho: F1 (F3, F4)
F1’ (F3’, F4’)
Trong đó F3, F3’ có cùng đường tác dụng với F2 và F2’; F4, F4’ hướng theo đường nối AC.
Hiển nhiên do tính đối xứng ta phải có F4 = F4’
Như vậy ngẫu lực
(F1, F1’) (F3, F3’) hay m1 = m2
Theo giả thiết ta có m1 = m2 m2 = m3 Mà m2 = F2 . d
m3 = F3 . d
Suy ra F2 = F3 ( điều phải chứng minh)
Định lý 2: Một ngẫu lực có thể dời đến mặt phẳng song song mà tác dụng của nó không thay đổi.
Định lý này được thừa nhận mà không chứng minh
Qua hai định lý trên cho thấy việc xác định một ngẫu lực không phụ thuộc vào vị trí cụ thể của mặt phẳng tác dụng cũng như hình dạng cụ thể ( phương, chiều, trị số các lực) của hai ngẫu lực đó. Để có hai ngẫu lực tương đương ta càn có
+ Mặt phẳng tác dụng song song với nhau
+ Cùng chiều quay
+ Cùng trị số
Đối với những ngẫu lực cùng nằm trong một mặt phẳng chỉ cần hai yếu tố
+ Cùng chiều quay
+ Cùng trị số
Nếu coi momen ngẫu lực là một giá trị đại số có dấu thì điều kiện này tương đương với
m1 = m2
Hệ quả:
Hệ quả 1: ngẫu lực có thể dời đến một vị trí tuỳ ý trong mặt phẳng tác dụng nếu giữ nguyên chiều quay và trị số của momen của nó
Hệ quả 2: Có thể thay đổi cánh tay đòn cũng như trị số của lực một cách tuỳ ý miễn là giữ nguyên trị số momen và chiều quay của nó.
3.2.3 Điều kiện cân bằng
a. Hợp hệ ngẫu lực phẳng:
Giả sử cho hệ ngẫu lực phẳng có mômen lần lượt là m1, m2, ... , mn (hình
1.36). Biến đổi hệ ngẫu lực này thành hệ ngẫu lực ( F1 , F1 ); ( F2 , F2 ); ... ; ( Fn , Fn ) có
cùng cánh tay đòn a.
Hợp lực
R của các lực F1 , F2 ,...,Fn
đặt tại A, B là hai lực song song, ngược
chiều, có cùng trị số:
R = RA = RB = F1 F2 ... Fn tạo thành ngẫu lực ( R, R )
Ngẫu lực ( R, R ) gọi là ngẫu lực tổng hợp, có mômen:
M = R.a = F1.a - F2.a + ... + Fn.a = m1 - m2 + ... + mn
Fn
F2
a
F1
R
F2
Fn
Hình 1.36
R
A B
F1
Như vậy: Một hệ ngẫu lực phẳng cho ta một hệ ngẫu lực tổng hợp có mômen bằng tổng đại số mômen của các ngẫu lực thuộc hệ.
Ví du:
n
M = mi
i1
Hệ ngẫu lực phẳng gồm m1 = 60 Nm; m2 = 120 Nm; m3 = -30 Nm.
- Hãy xác định ngẫu lực tổng hợp.
- Nếu ngẫu lực tổng hợp có cánh tay đòn là 0,5 m, trị số lực của nó bằng bao nhiêu?
Bài giải:
- Theo công thức tính ngẫu lực tổng hợp M ta có :
M = m1 + m2 + m3 = 60 + 120 - 30 = 150 Nm
- Theo công thức M = R.a R =
M 150 300N
a 0,5
Vậy: - Ngẫu lực tổng hợp là : M = 150 Nm
- Trị số ngẫu lực tổng hợp là: R = 300 N.
b. điều kiện cân bằng của hệ ngẫu lực phẳng:
n
Muốn hệ ngẫu lực phẳng cân bằng thì ngẫu lực tổng hợp của nó phải cân bằng, nghĩa là M = 0. Mà M = minên điều kiện cân bằng của hệ ngấu lực phải
i1
n
là: mi = 0
i1
Điều kiện cần và đủ để một hệ ngẫu lực phẳng cân bằng là tổng đại số mômen của các ngẫu lực thuộc hệ bằng 0.
Ví dụ: Dầm có hai gối đỡ A và B chịu tác dụng bởi ngẫu lực ( P, P ) có mômen m =
3.105 Nm.
NB
P
P
A B
2 m
NA
2 m
10 m
Xác định phản lực tại các gối đỡ của dầm.
Bài giải:
Ở hai gối đỡ có các phản lực tạo thành ngẫu lực cân bằng với ngẫu lực
( P, P ) cho nên theo điều kiện cân bằng ta có:
∑m = 0 P.10 - NB.6 = 0
NA
= NB =
P.10 3.10
5.104
N = 50 kN
5
6 6
Vậy phản lực tại hai gối đỡ của dầm là : NA = NB = 50 kN.
4. Hệ lực phẳng bất kỳ
4.1. Định nghĩa
y
B
→
NC
D
C
h
P
→NC
T
E
A→
x
Hệ lực phẳng bất kì là hệ lực gồm các lực có đường tác dụng nằm bất kỳ trong cùng một mặt phẳng.
Chẳng hạn, cần trục trên hình1 chịu tác
→ → →
dụng cuả hệ lực phẳng bất kỳ (P, Q, NB,
→ →
XA, YA).
Hệ lực phẳng bất kỳ là trường hợp tổng quát của hệ lực phẳng
Hình 1
4.2. Thu hệ lực phẳng bất kỳ về một tâm
4.2.1. Định lý dời lực song song
Khi dời song song một lực, để tác dụng cơ học không đổi phải thêm vào một ngẫu lực phụ có mô men bằng mô men của lực đối với điểm mới dời đến
F
O
A
F
F
A
O
F
F
A
O m
F
Lực
a) b) c)
Hình 2
F tác dụng tại A tương đương với tác dụng của nó tại O (lực
F ' ) và
một ngẫu lực có mômen bằng mômen của lực F đối với điểm O.
Chứng minh:
F F ' và m m0 (F )
Giả sử lực
F đặt tại A cần phải dời lực song song đến điểm O (Hình 2a).
Đặt tại O hai lực cân bằng ( ,
) có cùng trị số với lực (Hình 2b) thỏa mãn
F '
F '' F
các điều kiện sau:
F = F ' = F '' và
F // F ' // F ''
Ta có: F R ( F , F ' F '' )
Phân tích hệ lực ( F , F ' F '' ) có: F ' // cùng chiều và cùng trị số với F nên có thể
coi F ' là F dời từ A đến O. Còn F và F '' tạo thành ngẫu lực ( F , F '' ) có mômen
m = F.a, mặt khác m0( F ) = F.a nên m m0 (F ) (Hình 2c)
Như vậy F R F ' + m0( F ) định lý đã được chứng minh.
Định lý đảo: Một lực và một ngẫu lực cùng nằm trong một mặt phẳng tương đương với một lực song song cùng chiều, cùng trị số với lực đã cho và có mômen với điểm đặt của lực đã cho bằng mômen của ngẫu lực.
Từ định lý ta thấy lực tương đương phải có vị trí sao cho khi lấy mô men đối với điểm đặt của lực đã cho có dùng chiều quay của ngẫu lực và có cánh tay đòn a = m/F
4.2.2 - Thu gọn hệ lực phẳng bất kỳ về một tâm cho trước.
Giả sử cần phải thu hệ lực phẳng bất kỳ ( F1 , F2 , F3 ) (Hình 3a) về tâm O. Theo định lý dời lực song song, ta dời song song các lực đã cho về O (tâm thu gọn)
F F / và ngẫu lực m1 = mo( F )
1 1 1
F F / và ngẫu lực m2 = mo( F )
2 2 2
F F / và ngẫu lực m3 = mo( F )
3 3 3
F3
O
A
C
B
F2
F3
F1
m3
m1
m2
F2
R
O
Tại điểm mới dời đến O hệ lực đã cho tương đương với một hệ lực phẳng đồng quy và một hệ ngẫu lực phẳng (Hình 3b).
F
M
o
1
a) b) c)
Hình 3.
Thu hệ lực phẳng đồng quy ( F / , F / , F / ) được R /
1 2 3
Thu hệ ngẫu lực phẳng được ngẫu lực có mô men: Mo = m1 + m2 + m3 =
mo( F1 ) + mo( F2 ) + mo( F3 ) = mo F .
R / được gọi là véctơ chính còn Mo được gọi là mômen chính của hệ ngẫu
lực phẳng đã cho đối với điểm O.
Vậy ”Hệ lực phẳng bất kỳ tương đương với một lực có véc tơ bằng véctơ chính của hệ lực và một ngẫu lực có mômen bằng mômen chính của hệ lực đối với tâm thu gọn”.
- Xác định Véctơ chính. Vì hình chiếu
F / , F / , F /
và F , F , F luôn
bằng nhau nên ta có:
1 2 3
1 2 3
+Trị số của
+ Hướng của
R / :
R / :
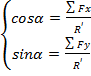
M = m
- Xác định mômen chính.
o o F
Từ công thức trên cho chúng ta thấy:
Vec tơ chính không phụ thuộc vào tâm thu gọn
Mô men chính thay đổi theo tâm thu gọn ( vì với mỗi tâm thu gọn khác nhau lực có cánh tay đòn và chiều quay khác nhau)
4.3. Điều kiện cân bằng của hệ lực phẳng bất kỳ
4.3.1. Điều kiện cân bằng
Điều kiện cần và đủ để một hệ phẳng bất kỳ cân bằng là véc tơ chính và mô men chính của hệ đối với một tâm bất kỳ đều phải đồng thời bằng không.
R’ = 0
Mo = 0
4.3.2. Các dạng phương trình cân bằng
* Dạng 1: Điều kiện cần và đủ để một hệ phẳng bất kỳ cân bằng là tổng hình chiếu của các lực nên hai trục tọa độ vuông góc và tổng đại số mô men của các lực đối với một tâm bất kỳ trên mặt phẳng đều bằng không.
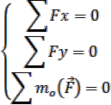
Thật vậy theo điều kiện R’ = 0 và Mo = 0
R có hai hình chiếu lên trục x và y.
Rx = ∑Fx