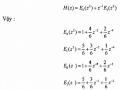Cho x(n) = rect3(n)
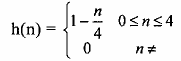
Giải
Giải bằng đồ thị cho trên hình 3.3.3.4.
Có thể bạn quan tâm!
-
Thay Đổi Nhịp Lấy Mẫu Với Hệ Số M -
Xử lý tín hiệu số 2 Phần 2 - 4 -
Bộ Lọc Biến Đổi Nhịp Lấy Mẫu Với Hệ Số M L -
Xử lý tín hiệu số 2 Phần 2 - 7 -
Cấu Trúc Nhiều Pha Của Bộ Lọc Lấy Mẫu -
Cấu Trúc Nhiều Pha Của Các Bộ Lọc Biến Đổi Nhịp Hệ Số M/l Không Nguyên
Xem toàn bộ 140 trang tài liệu này.
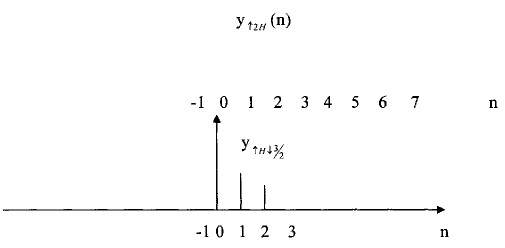
Hình 3.3.3.4
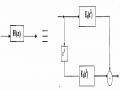
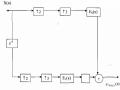
c) Biểu diễn phép lọc biến đổi nhịp trong miền z
Trong miền z phép lọc biến đổi nhịp được mô tả như sau:
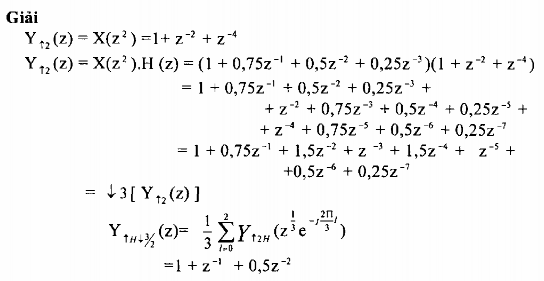
d) Biểu diễn phép lọc biến đổi nhịp trong miền tần số
Đánh giá X(z) ,H (z),YLH(z) và YHM/L (z) trên vòng tròn đơn vị trong mặt phẳng z, z ta sẽ có biểu diễn phép lọc biến đổi nhịp trong miền tần số như sau:
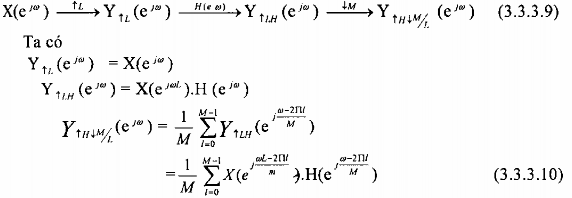
Ví dụ 3.3.3.3
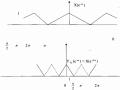
Cho tín hiệu x(n) có X(ej) cho trên hình 3.3.3.5 (a) hãy tìm cách giảm nhịp lấy mẫu
3
2
3
2
đi lần ,tức là nén tín hiệu x(n) lại lần nhưng không được làm mất thông tin chứa
trong x(n)
Giải
Vì phổ X(ej) có bề rộng -
2- < <
3
2vậy ta có thể dung bộ lọc biến đổi nhịp
3
H
3, M=3 ,L=2 , ta chọn tần số cắt c của bộ lọc H(ej) là
2
= có như vậy sẽ
M 3
không làm mất thông tin của x(n) hình 3.3.3.5 sẽ minh hoạ cho ta rõ.
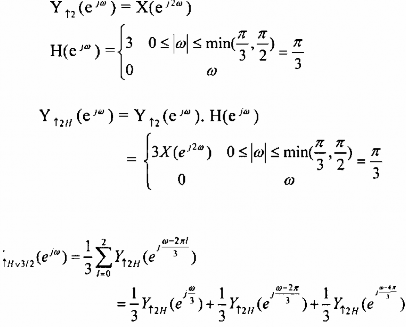
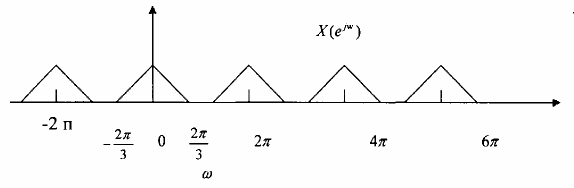
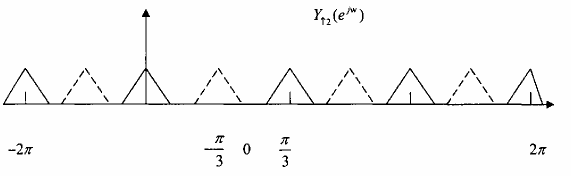
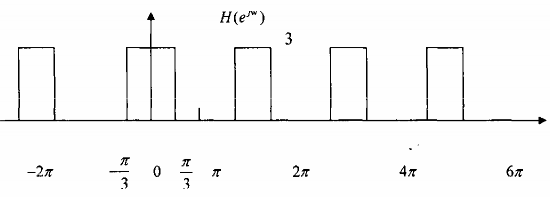
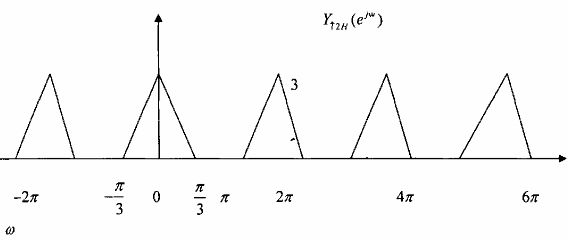
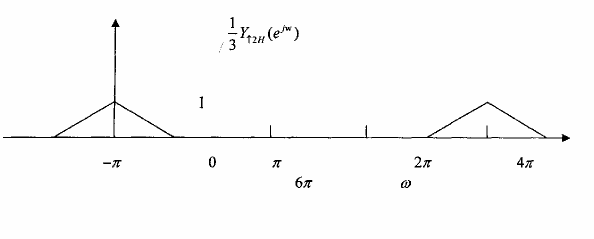
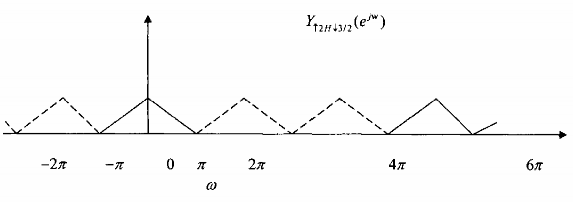
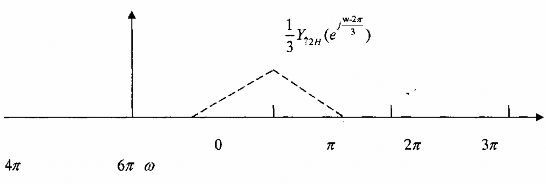
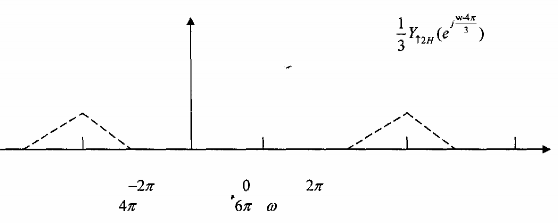
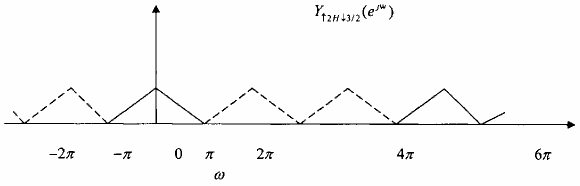
Hình 3.3.3.5
3.4. PHÂN HOẠCH NHIỀU PHA (POLYPHASE DECOMPOSITION)
3.4.1. PHÂN HOẠCH NHIỀU PHA HAO THÀNH PHẦN
a) Phân hoạch hàm truyền đạt H(z) .
Ta biết một hệ thống tuyến tính bất biến có đáp ứng xung là:
Và có hàm truyền đạt là H(z):
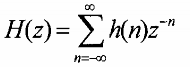
Bây giờ ta phân đãy h(n) làm hai phần ứng vời n chẵn và n lẻ,vậy ta có:
h(n) h(2r) và h(2r + 1)
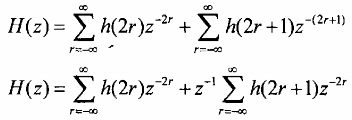
Gọi e0(r) = h(2r) và e1(r) = h(2r +1)
và đặt
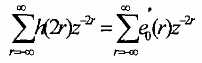
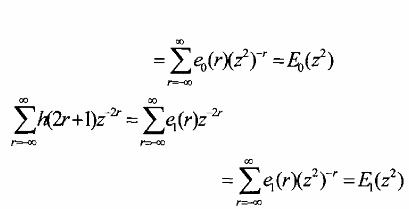
cuối cùng ta có:
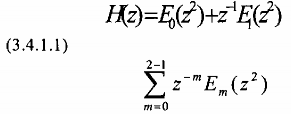
Việc biểu diễn H(z) dưới dạng (3.4.1.1) này gọi là phân hạch nhiều pha hai thành phần của H(z). Hay nói cách khác, chúng ta đã biểu diễn H(z) ở dạng nhiều pha hai thành phần. E0(z2) và E1(z2) được gọi là các thành phần nhiều pha của H(z) và ta cũng có: E0(z) và E1(z) cũng được gọi là các thành phần nhiều pha của H(z).
Một tính chất quan trọng của phân hoạch nhiều pha hao thành phần đó là:
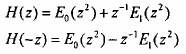
Vậy
(3.4.1.2)
Hay:
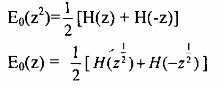
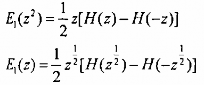
Ví dụ 3.4.1.1
Cho bộ lọc số IIR có đáp ứng xung như sao:
H(n) = anU(n)
Hãy tìm phân hoạch nhiều pha hai thành phần của H(z)
Giải
Ta phân h(n) thành hai thành phần đáp ứng với n chẵn và n lẻ, sao đó lấy biến đổi Z
ta có:
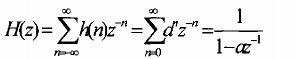
|z| > |a|
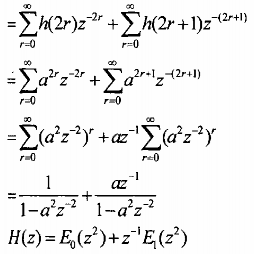
Vậy
Từ đây ta có:
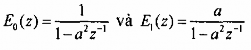
Ví dụ 3.4.1.2
Cho bộ lọc số FIR pha tuyến tính có đáp ứng xung như sau:
H(n) = {1, 2, 3, 4, 3, 2, 1}