Hình 3.2.3.6
Nhận xét
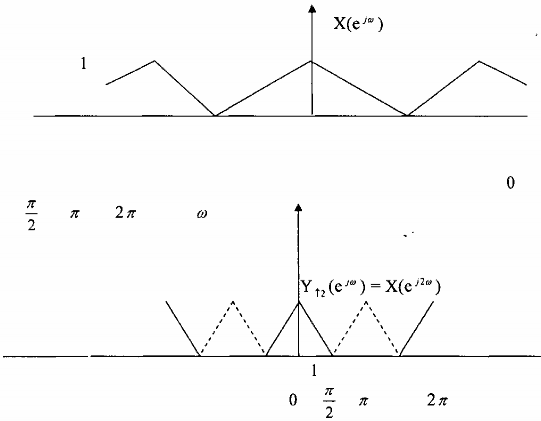
- Y L (ej) là bản ảnh (version) co hẹp L lần của X(ej), nhưng lại xuất hiện (L - 1 ) bản sao chụp phổ cơ bản, (L - 1 ) bản sao chụp phụ này là các ảnh được tạo ra bởi bộ nội suy hệ số L. Hiện tượng xuất hiện các bản sao chụp phụ này gọi là hiệu ứng tạo ảnh (imaging)
- Từ ví dụ với L = 2 ở trên ta thấy rằng hiệu ứng tạo ảnh này không gây hiện tượng chồng phổ và như vậy nó không làm mất thông tin.
- Phép nội suy làm tín hiệu xâu giãn rộng trong miền thời gian (nếu n là thời gian) thì sẽ dẫn đến hiện tượng co hẹp trong miền tần số, đây là tính chất của biến đổi Fourier.
- Phép nội suy tấm chèn. thêm (L - 1 ) mẫu có biên độ 0 vào gì ~ a hai mẫu của xâu thì trong miền tần số sẽ tạo ra (L -1 ) bản sao chụp phụ phổ cơ bản, tức là L-l bản sao chụp này sẽ chèn vào giữa hai phổ cơ bản.
- Từ nội suy ở đây có nghĩa là nếu tín hiệu xâu với tần số lấy mẫu Fs sau khi qua bộ nội suy sẽ có tần số lấy mẫu F's = LFS và với các mẫu có biên độ 0. Sau đó ta cho qua bộ
lọ có tần số cắt là
Có thể bạn quan tâm!
-
Xử lý tín hiệu số 2 Phần 2 - 1 -
Xử lý tín hiệu số 2 Phần 2 - 2 -
Xử lý tín hiệu số 2 Phần 2 - 4 -
Bộ Lọc Biến Đổi Nhịp Lấy Mẫu Với Hệ Số M L -
Phân Hoạch Nhiều Pha (Polyphase Decomposition)
Xem toàn bộ 140 trang tài liệu này.
thì ở đầu ra của bộ lọc ta sẽ thu được tín hiệu với tần số lấy mẫu LFs
L
nhưng các mẫu biên độ 0 đã được nội suy từ các mẫu biên độ khác 0 của xâu, tức là ta có tín hiệu xâu có tần số lấy mẫu LFs với các mẫu biên độ khác 0, quá trình nội suy này được thực hiện bằng mạch lọc nội suy mà ta sẽ nghiên cứu kỹ ở phần sau.
3.2.4. THAY ĐỔI NHỊP LẤY MẪU VỚI HỆ SỐ M
L
a) Biểu diễn trong miền tần số n
Trong kỹ thuật nhiều khi để thực hiện một nhiệm vụ nào đó chúng ta cần phải thay
đổi nhịp lấy mẫu với hệ số là phân số
M . Để thực hiện nhiệm vụ này chúng ta sẽ ghép
L
nối tiếp giữa hai bộ nội suy và phân chia với nhau hoặc theo thứ tự ngược lại, bộ này ta
gọi là bọ biến đổi nhịp với hệ số
M . Xem hình 3.2.4.1.
L
Ta thấy rằng tần số lấy mẫu Fs của tín hiệu vào xâu sau khi qua khỏi bộ biến đổi nhị
với hệ số
M thì tần số lấy mẫu sẽ bị thay đổi
L
M lần tức là:
L
F’s =
L Fs (3.2.4.1)
M
Hoặc Chu kỳ lấy mẫu sẽ thay đổi
M lần:
L
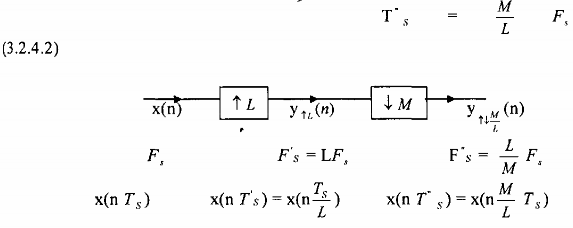
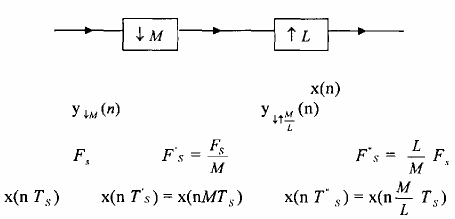
Hình 3.2.4.1
Chúng ta có thể dùng ký hiệu toán tử để biểu diễn phép biến đổi nhịp lấy mẫu hệ số
M như sau
L
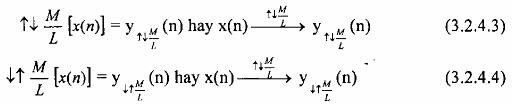
Để thuận tiện ta ký hiệu lại bộ biến đổi nhịp hệ số
M như hình 3.2.4.2. Nếu mũi
L
tên lên dặt trước mũi tên xuống thì tức là bộ nội suy đặt trước bộ phân chia. Còn nếu mũi tên xuống đặt trước mũi tên lên thì tức là bộ phân chia đặt trước bộ nội suy.
Trong hệ số
M thì tử số là hệ số của bộ phân chia, mẫu số là hệ số của bộ nội suy.
L
Sở dĩ ta phải phân biệt trước sau giữa bộ phân chia và bộ nội suy bởi vì phép phân chia và nội suy không có tính chất giao hoán. Bộ phân chia, bộ nội suy và bộ biến đổi nhịp là những hệ thống không phải là bất biến theo biến số n, tức là, chúng là các hệ thống thay đổi theo n (nếu n là thời gian, thì là thay đổi theo thời gian).
Như vậy nói chung thì
y M(n) ≠
L
y M(n)
L
mặc dù tỉ lệ thay đổi nhịp lấy mẫu đều là
M . Tuy nhiên cũng có trường hợp
L
một số điêu kiện (ta sẽ xét sau).
y M(n) =
L
y M(n)
L
nếu quan hệ giữa M và L thỏa mãn
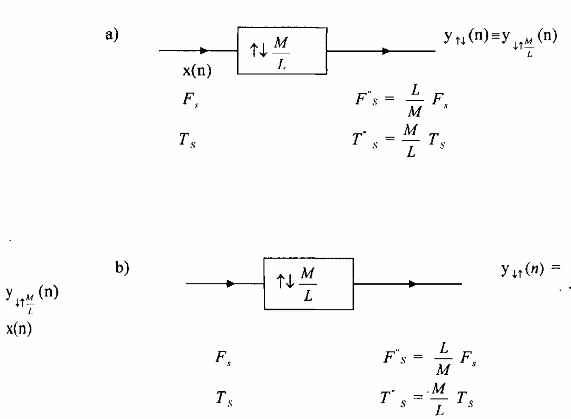
a) bộ biến đổi nhịp M
L
b) bộ biến đổi nhịp M
L
hình 3.2.4.2
nếu M > L thì bộ thay đổi nhịp làm nhiệm vụ nén tín hiệu theo tỷ lệ M
L
nếu M < L thì bộ thay đổi nhịp làm nhiệm vụ giãn tín hiệu theo tỷ lệ M
L
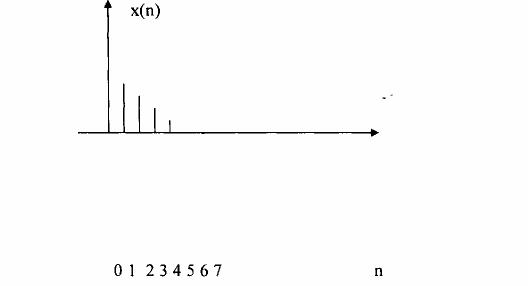
Ví dụ 3.4.2.1
Cho x(n) như sau
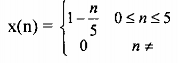
Giải
x(n) đi qua bộ biến đổi nhịp lấy mẫu với hệ số
a) bộ biến đổi nhịp M
L
b) bộ biến đổi nhịp M
L
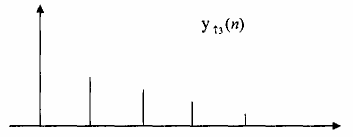
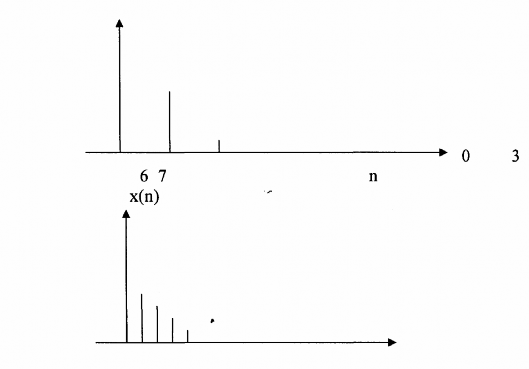
M = 2 . Hãy vẽ tín hiệu ra y(n) với:
L 3
Ta giải bằng đồ thị, xâu được chuẩn hóa bởi T’s =
2 Ts
3
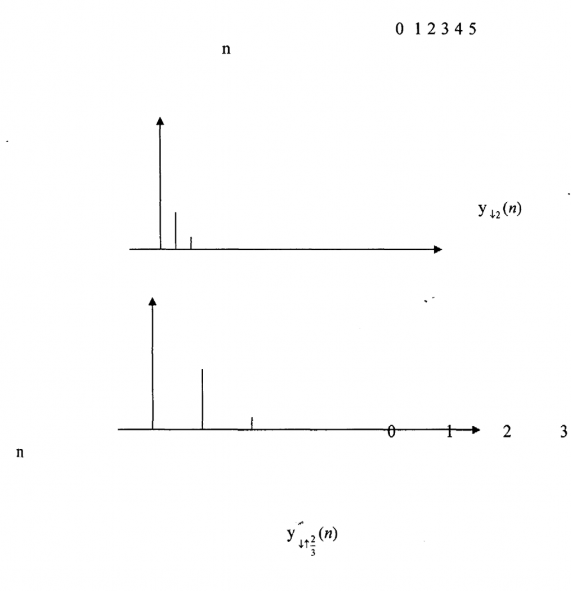
Nhận xét:
- Trong trường hợp của ví dụ 3.2.4.1 ta thấy rằng nếu M = 2, L= 3 thì
(không nhìn thấy vì phô tô mờ)
n0L = n1 M+ 1 n0 và n1 là các số nguyên hoặc:
y M(n) .....
L
n1M = n0L+1
Thì
Ta có thể ký hiệu sự tương đương này như sau:
y M(n) =
L
y M(n)
L
y M(n) ≡
L
y M(n)
L
(3.2.4.5)
Nếu L và M thỏa mãn điều kiện:
n0L – n2M = 1
Hoặc:
n1M – n0L = 1
(3.2.4.6)
ở đây n0 và n1 là các số nguyên.
(3.2.4.6) chính là nội dung của định lý Euclid.
b) Biểu diễn trong miền z
Trong phần này ta sẽ dùng biến đổi z để nghiên cứu quan hệ vào ra của các bộ biến đổi nhịp, và cũng từ đây chúng ta sẽ giải thích được nhiều tính chất của phép biến đổi nhịp lấy mẫu.
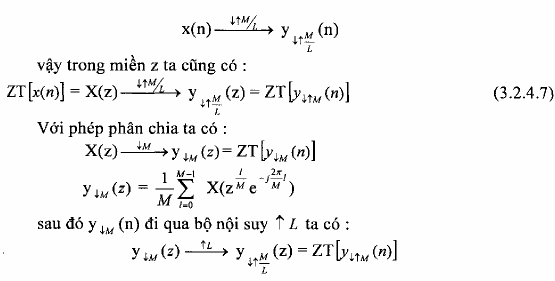
Trước tiên ta xét quan hệ vào ra của bộ biến đổi nhịp nhịp như sau:
y M(n) , ta có phép biến đổi
L
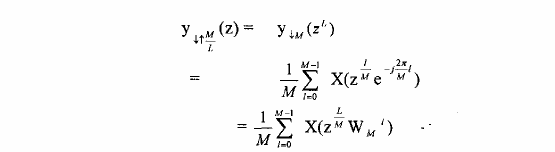
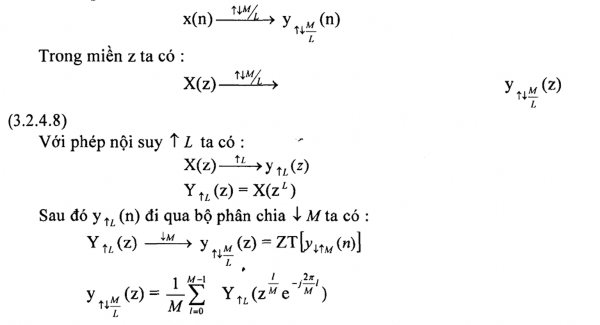
Bây giờ ta xét quan hệ vào ra của bộ biến đổi nhịp nhịp như sau:
y M(n) , ta có phép biến đổi
L
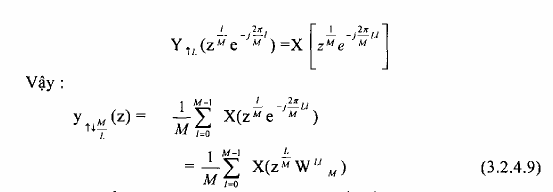
- Dựa vào biểu thức
y M(z)
L
và Y↑↓(z) ta thấy rằng
y M(z) ≠
L
y M(z) , tức là nói
L
chung
y M(n) ≠
L
y M(z) , như mục trên chúng ta có nhận xét.
L
- Nhưng cũng có những khả năng
y M(z) =
L
y M(z)
L
nếu: