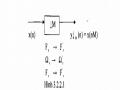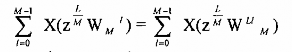
1
1 L1 L1
Điều này có thể xảy ra nếu và chỉ nếu WM = W M hoặc tập hợp M số hạng W M
trùng với tập hợp M số hạng WM với 0 ≤ l ≤ M - 1.
-Trong trường hợp 1 = M ta có:
Có thể bạn quan tâm!
-
Xử lý tín hiệu số 2 Phần 2 - 1 -
Xử lý tín hiệu số 2 Phần 2 - 2 -
Thay Đổi Nhịp Lấy Mẫu Với Hệ Số M -
Bộ Lọc Biến Đổi Nhịp Lấy Mẫu Với Hệ Số M L -
Phân Hoạch Nhiều Pha (Polyphase Decomposition) -
Xử lý tín hiệu số 2 Phần 2 - 7
Xem toàn bộ 140 trang tài liệu này.
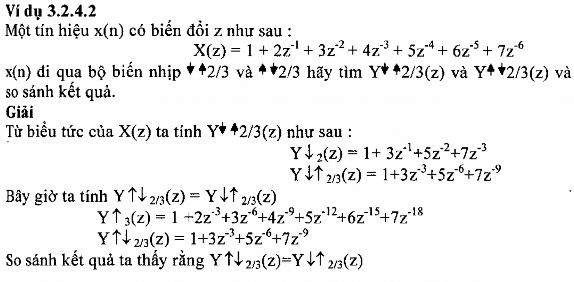
c) Biểu diễn phép biến đổi nhịp trong miền tần số
Đánh giá X(z), Y↑↓M/L(z) và Y↓↑M/L(z) trên vòng tròn đơn vị trong mặt phẳng z ta
có:
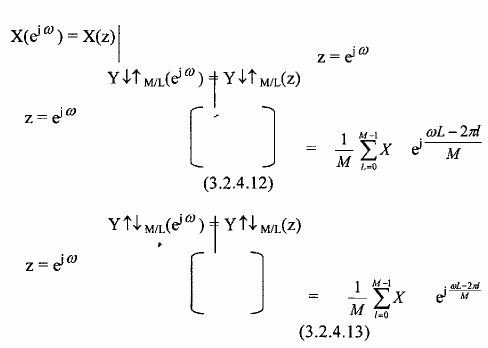
Ví dụ 3.2.4.3
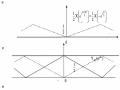
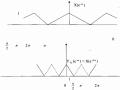
Cho tín hiệu xâu có phổ là như trên hình 3.2.4.4 sau đây:
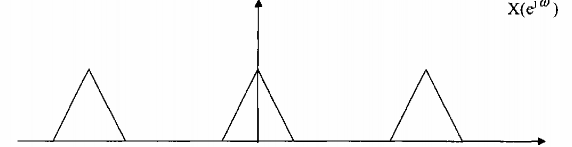
Giải
Hình 3.2.4.4
Giải bằng đồ thị trên hình 3.2.4.4 sau đây:
Từ hình 3.2.4.4 ta thấy rằng Y↓↑2/3(ej) = Y↑↓2/3(ej)
3.3. BỘ LỌC BIẾN ĐỔI LẨY MẪU
3.3.1. BỘ LỌC PHÂN CHIA
a) Tổng quan
Ở phần trên ta đã nghiên cứu phép phân chia và bộ phân chia, kết quả cho thấy tín hiệu x(n) khi đi qua bộ phân chia ↓M, trong miền tần số sẽ tạo ra M-1 thành phần hư danh (alíaing), các thành phần hư danh này sẽ gây hiện tượng chồng phổ, Nhưng nếu x(n)
có band tần nằm trong khoảng
M M
tức là tần số giới hạn dải chắn ( Stopband edge)
L
sẽ gây hiện tượng chồng phổ
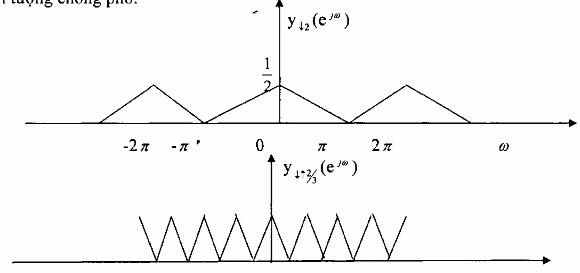
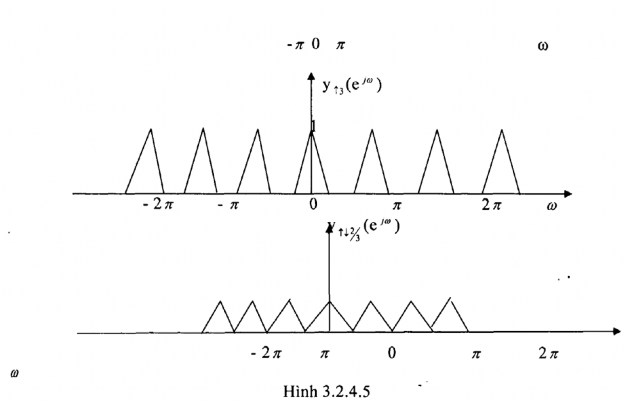
Để làm điều này chúng ta có thể đặt trước bộ phân chia ↓M một bộ lọc thông thấp
có c M
Bộ lọc thông thấp này làm nhiệm vụ loại bỏ các thành phần tần số ta sẽ tránh được hiện tượng chồng phổ.
M
như vậy
Sơ đồ tổng quát của bộ lọc phân chia cho trên hình 3.3.1.1
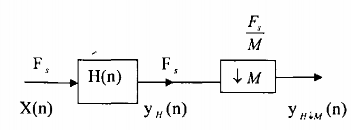
h(n): đáp ứng xung của bộ lọc
Hình 3.3.1.1
Để ngắn gọn chúng ta có thể dùng cách biểu diễn toán tử như sau:
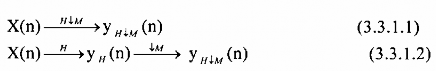
b) Biểu diễn phép lọc phân chia trong miền biến số n
Các phép toán trong phép lọc phân chia xảy ra như sau trong miền biến số n:
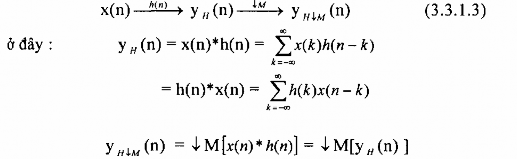
Cần lưu ý một điều là phép chia không có tính chất phân phối vào phép chập, tức là:
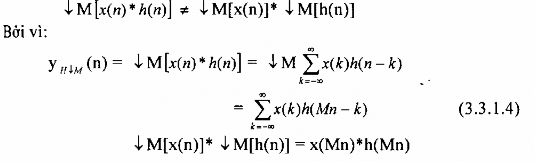
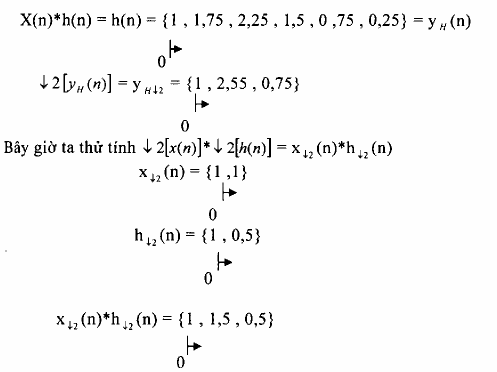
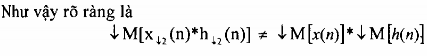
c) Biểu diễn phép lọc phân chia trong miền z
Trong miền z phép lọc phân chia được mô tả như sau:
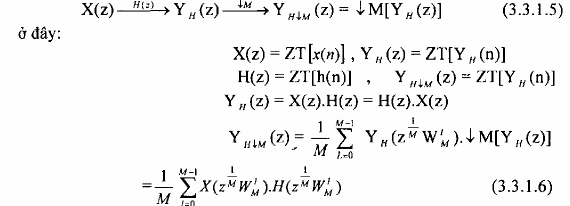
Cũng như trong miền biến số n ta lưu ý một điều là phép phân chia không có tính chất phân phối vào phép nhân trong miền z tức là:
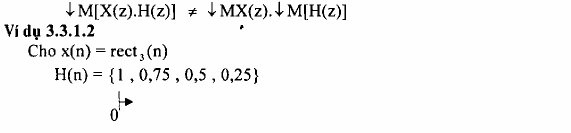
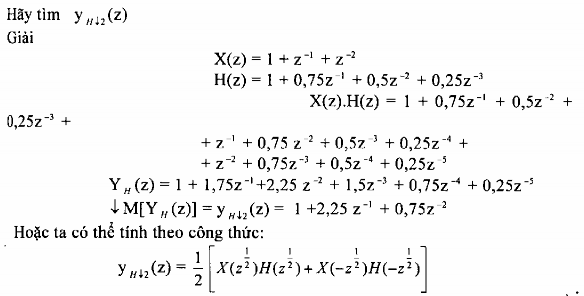
Chú ý: Xét phép lọc phân chia sau đây:
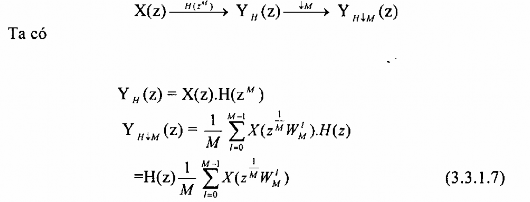
Bây giờ ta xét phép lọc phân chia sau đây:
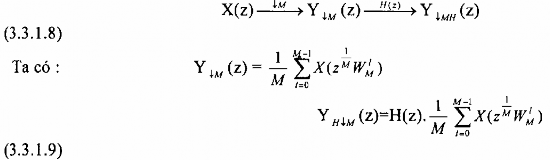
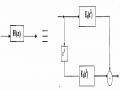
Ta thấy rằng YH↓M(z) = Y↓MH(z) vậy hai phép lọc này là tương đương nhau. Do đó sơ đồ thực hiện hai phép này là đồng nhất, xem hình 3.3.1.2
a) b)
Hình 3.3.1.2
- Sự đồng nhất của hai sơ đồ (a) và (b) trên hình 3.3.1.2 là rất có giá trị trong các
ứng dụng thực tế để thực hiện các bộ lọc và các bank lọc.
- Để ngắn gọn ta kí hiệu phép lọc trên hình 3.3.1.2 (a) và (b) là |H(zM) ↓ M| và
|↓MH(z)|. Vậy ta có thể viết:
(3.3.1.10)
H(zM)↓M ≡ ↓MH(z)
d) Biểu diễn phép lọc phân chia trong miền tần số
đánh giá X(z), H(z) và Y H↓M (z) trên vòng tròn đơn vị trong mặt phẳng z ta có sẽ có cách biểu diễn phép lọc phân chia trong miền tần số như sau:
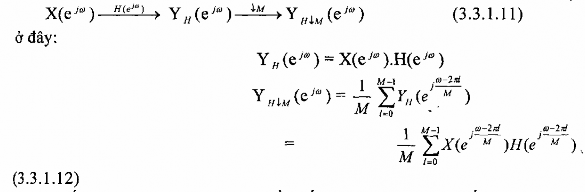
Nếu YH(ej) là đáp ứng tần số của bộ lọc thông thấp lý tưởng có
c M
thì các
thành phần hư danh sẽ không gây hư thông tin, tức là không có hiện tượng chồng phổ. Do
đó ta có thể tách thành phần đầu tiên (I = 0 ) ra mà dạng của nó sẽ không bị méo:
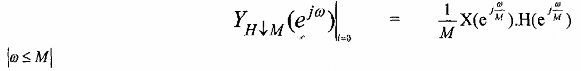
và nếu H(ej) là bộ lọc thông thấp lý tưởng tức là ổ dải thông |H(ej)|=1 dải chắn
|H(ej)|=0 thì ta có thành phần đầu tiên (I = 0) như sau:
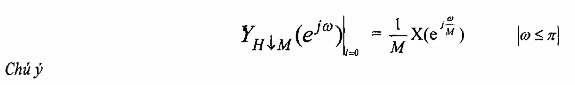
Trong ví dụ trên ở bộ phân chia ↓M = 2 đã không gây hiện tượng chồng phổ, bởi vì
tần số ωs của bộ lọc thông thấp bằng
, nó đã cắt bỏ đi thành phần tần số cao
2
.
2
Vậy nếu thông tin của chúng ta chỉ chứa trong thành phần phổ
2
thì bộ lọc sẽ không
làm mất mát thông tin. Còn nếu thông tin của chúng ta có chứa cả trong các thành phần
phổ có ta.
2
thì việc cắt bỏ thành phần tần số cao đã làm mất mát thông tin của chúng
e) Tính chất của phép lọc phân chia
Nếu
Thì
H(z) = H1(z) + H2(z)
YH (z) = Y(z)[ H1 (z) + H2 (z)]
= X(z). H1 (z) + X(z). H2 (z)
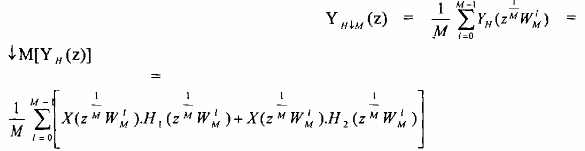
= ↓ M[X(z).H1 (z)]+ ↓ MX(z).H2 (z)] (3.3.1.13)
Vậy phép phân chia có tính phân phối vào phép cộng
3.3.2. BỘ LỌC NỘI SUY
a) Tổng quan
Chúng ta đã nghiên cứu phép nội suy và bộ nội suy, kết quả phép nội suy đã chèn thêm