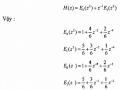Giải
0
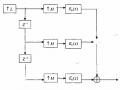
Hãy tìm phân hoạch nhiều pha hai thành phần của H(z).
Phân h(n) thành hai thành phần ứng với n chẵn và n lẻ và lấy biến đổi Z ta có :
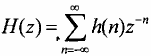
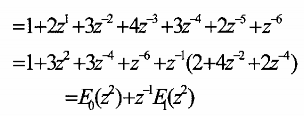
Có thể bạn quan tâm!
-
Xử lý tín hiệu số 2 Phần 2 - 4 -
Bộ Lọc Biến Đổi Nhịp Lấy Mẫu Với Hệ Số M L -
Phân Hoạch Nhiều Pha (Polyphase Decomposition) -
Cấu Trúc Nhiều Pha Của Bộ Lọc Lấy Mẫu -
Cấu Trúc Nhiều Pha Của Các Bộ Lọc Biến Đổi Nhịp Hệ Số M/l Không Nguyên -
Một Vài Ứng Dụng Của Hệ Thống Lọc Số Nhiều Nhịp
Xem toàn bộ 140 trang tài liệu này.
ở đây
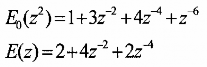
vậy ta cũng có :
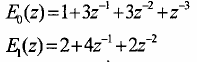
b)Cấu trúc nhiều pha hai thành phần
Định nghĩa: Cấu trúc thực hiện biểu thức của H(z) dưới dạng phân hoạch nhiều pha
được gọi là cấu trúc nhiều cha của hệ thống số.
Ta đã có dạng nhiều pha hai thành phần của H(z) như sau:
H(z) = E0(z2) + z-1E1(z2)
Từ đây ta có thể vẽ sơ đồ cấu trúc nhiều pha tổng quát như trấn hình 3.4.1.1
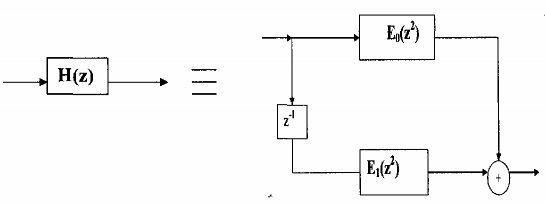
Hình 3.4.1.1
Ví dụ 3.4.1.3
Cho bộ lọc số FIR pha tuyến tình có hàm truyền đạt H(z) ở dạng phân hoạch nhiều pha hai thành phần sau:
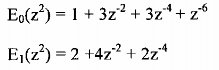
Giải
Hãy vẽ cấu trúc nhiều pha của H(z).
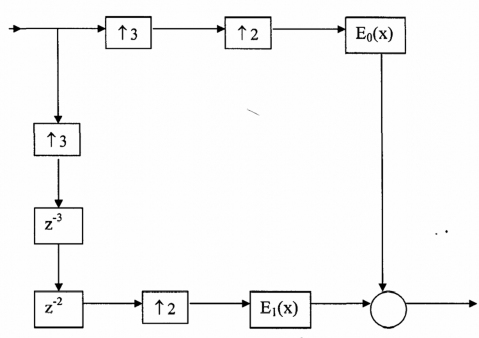
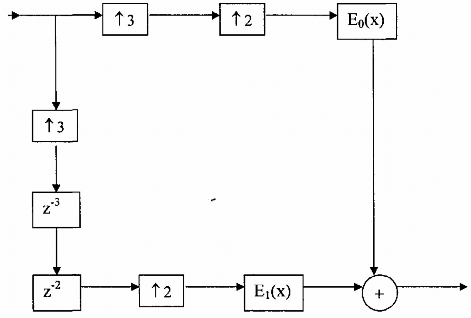
Vì là pha tuyến tính nên e0(r) và e1(r) là đối xứng,cấu trúc nhiều pha của H(z) pha
tuyến tính được cho bởi hình 3.4.1.2.
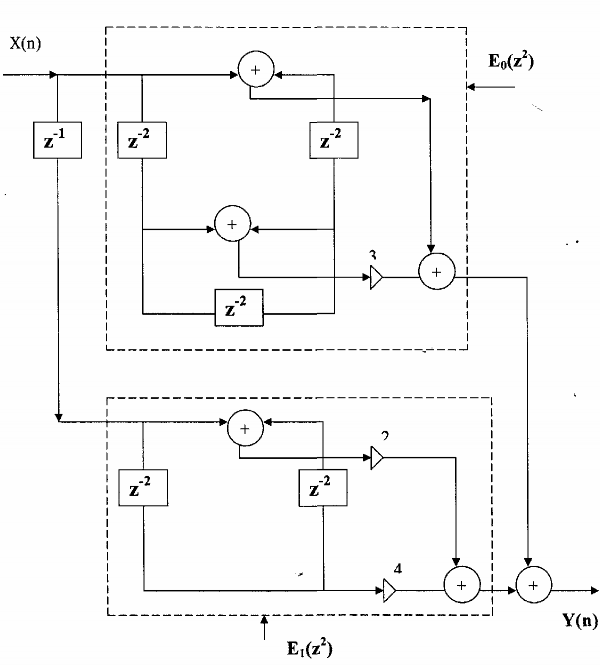
Hình 3.4.1.2
3.4.2. PHÂN HOẠCH NHIỀU PHA M THÀNH PHẦN
a) Phân hoạch hàm truyền đạt H(z)
Bây giờ ta xét trường hợp tổng quát tức là biểu diễn H(z) ở dạng nhiều pha M thành phần.
Tương tự như trên ta cũng có thể phân h(n) thành M thành phần như sau:
H(n) h(Mr), h(Mr + 1), ..., h[Mr + (M – 1)]
Vậy hàm truyền đạt H(z) sẽ có dạng như sau:
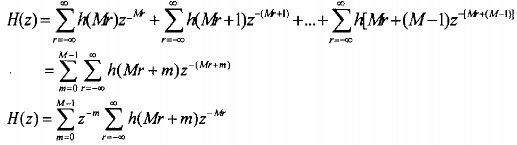
Đặt
Vậy
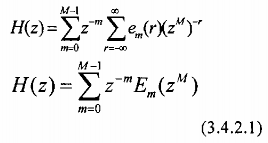
ở đây
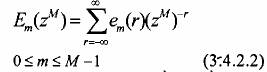
Em(zM) được gọi là các thành phần nhiều pha của H(z). Ta cũng rút ra được biểu thức sau:
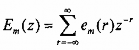
0 m M -1 (3.4.2.3)
Việc biểu diễn H(z) dưới dạng (3.4.2.3)gọi là phân hoạch nhiều pha M thành phần của H(z).
Ví dụ 3.4.2.1
Cho bộ lọc số IIR có đáp ứng xung như sau:
H(n) = anU(n)
Hãy tìm phân hoạch nhiều pha M = 3 thành phần của H(z)
Giải
Phân h(n) thành ba phần ứng với n = 3r, n = 3r + 1, n = 3r + 2, và lấy biến đổi Z
h(n) ta có:
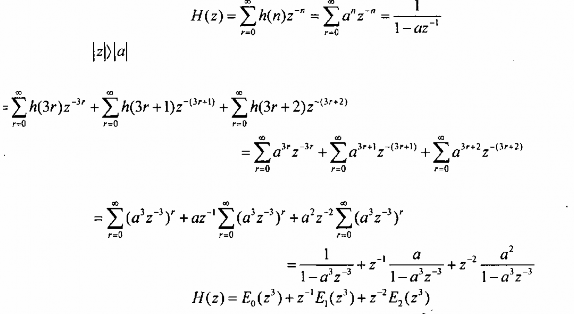
Vậy
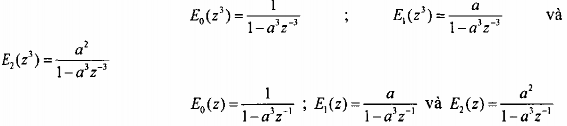
Ví dụ 3.4.2.2
Cho bộ lọc số FIR pha tuyến tính có đáp ứng xung như sau:
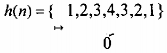
hãy tìm phân hoạch nhiều pha M = 3 thành phần của H(z).
Giải
Phân h(n) thành 3 thành phần ứng với n = 3r, n = 3r + 1, n = 3r + 2 và lấy biến đổi z ta có:
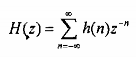
= 1 + 2z-1 + 3z-2 + 4z-3 + 3z-4 + 2z-5 + z-6
ở đây:
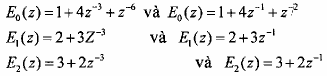
Từ cách biểu diễn H(z) ở dạng nhiều pha M thành phần chúng ta có thể rút ra một tính chất quan trọng như sau:
Ta đã có:
Lấy biến đổi zM hai vế ta có :
Đổi biến số:
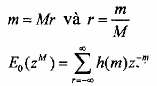
Với m = Mr, r: nguyên
Ta đã có định nghĩa dãy p(m) như sau:
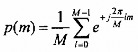
Với m = M.n, n: nguyên Từ đây ta có:
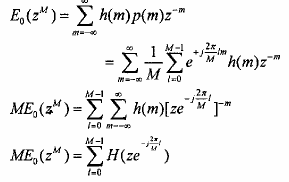
Hoặc
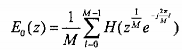
b) Cấu trúc nhiều pha M thành phần
Phân hoạch nhiều pha M thành phần của H(z) là cơ sở để xây dựng cấu trúc nhiều
pha M thành phần, mà hàm truyền đạt của cấu trúc này là H(z).
Hình 3.4.2.1 minh họa cấu trúc nhiều pha M thành phần tổng quát để thực hiện hàm
H(z):
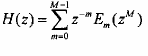
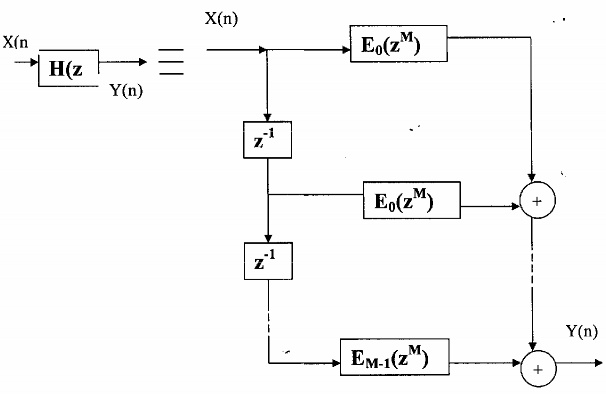
Hình 3.4.2.1
Ví dụ 3.4.2.3
Cho bộ lọc số IIR của hàm truyền đạt H(z) cho ở dạng phân hoạch nhiều pha 3 thành phần như sau:
H(z) = E0(z3) + z-1E1(z3) + Z-2E2 (z3)
thì kết quả là tương đương nhau, kết quả ta thu được như cấu trúc hình 3.5.3.7 (a), (b), và (c).
