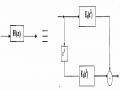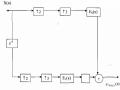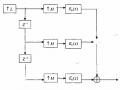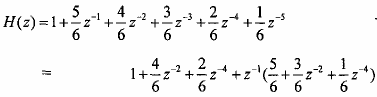
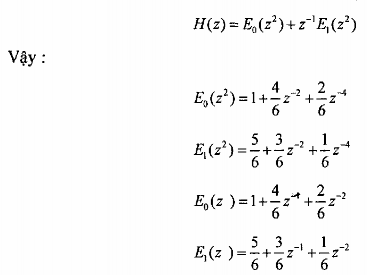
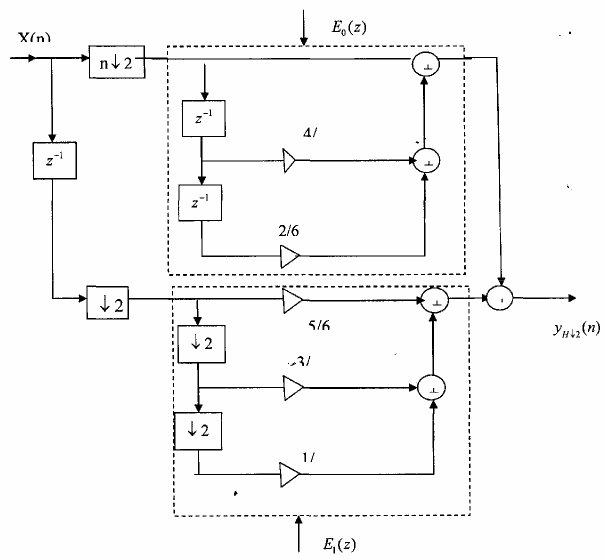
Từ đây ta có cấu trúc nhiều pha hai thành phần tối ưu nhất của FIR H2 minh hoạ trên hình 3.5.1.5 (a) và 3.5.1.5 (b).
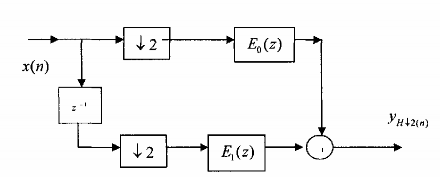
Hình 3.5.1.5
Có thể bạn quan tâm!
-
Phân Hoạch Nhiều Pha (Polyphase Decomposition) -
Xử lý tín hiệu số 2 Phần 2 - 7 -
Cấu Trúc Nhiều Pha Của Bộ Lọc Lấy Mẫu -
Một Vài Ứng Dụng Của Hệ Thống Lọc Số Nhiều Nhịp -
Xử lý tín hiệu số 2 Phần 2 - 11 -
Xử lý tín hiệu số 2 Phần 2 - 12
Xem toàn bộ 140 trang tài liệu này.
Hình 3.5.1.5
3.5.2. Cấu trúc nhiều pha của bộ lọc nội suy
Chúng ta sẽ dùng cấu trúc nhiều pha loại 2 cho trên hình 3.4.3.1 để xây dựng cấu trúc nhiều pha L thành phần của bộ lọc nội suy hệ số L LH.Kết hợp với h ình 9.3.2.1 ta nhận được bộ lọc nội suy LH có cấu trúc nhiều pha L thành phần được minh hoạ trên hình 3.5.2.1.
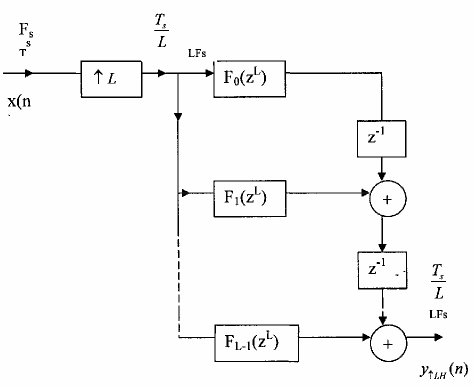
Hình 3.5.2.1
Nhận xét:
- Cấu trúc trên hình 3.5.2.1 không nói lên được sự ưu việt của các cấu trúc nhiều pha vì nó dựa trên cấu trúc trên cơ sở cấu trúc 3.3.2.1.
- Bộ lọc nội suy hệ số LTLM sẽ được xây dựng trên cơ sở cấu trúc nhiều pha L thành phần, như vậy nó sẽ bị lợi dụng được sự đồng nhất của 2 sơ đồ (a) và (b) trên hình 3.3.2.2.
Do phép nội suy có tính chất phân phối vào phép cộng nên ta có thể chuyển cấu trúc trên hình 3.5.2.1 thành cấu trúc trên hình 3.5.2.2 mà kết quả vẫn như nhau.
Sử dụng sự đồng nhất của hai sơ đồ (a) và (b) trên hình 3.3.2.2 ta sẽ chuyển cấu trúc trên hình 3.5.2.2 thành cấu trúc trên hình 3.5.2.3.
Cấu trúc nhiều pha L thành của bộ lọc nội suy LH cho trên hình 3.5.2.3 là cấu trúc ưu việt nhất. Để thay được nhưng ưu điểm của cấu trúc nhiều pha loại này chúng ta hãy so sánh với cấu trúc trực tiếp bộ lọc nội suy TLH. Chúng ta lấy bộ lọc FIR có chiều dài N làm ví dụ minh họa. Cấu trúc trực tiếp của LH cho trên hình 3.5.2.4. Ta có thể tắt bộ lọc nội suy FIR là FIR LH. Bây giờ ta tiến hành so sánh.
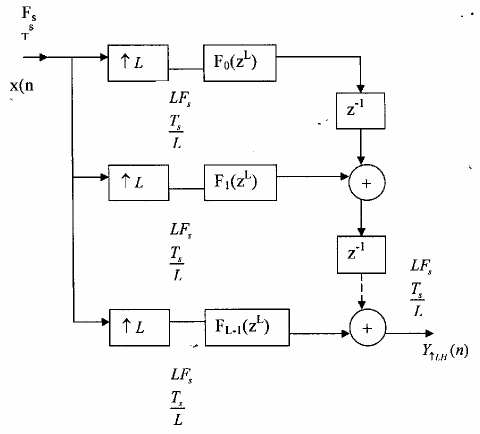
Hình 3.5.2.2
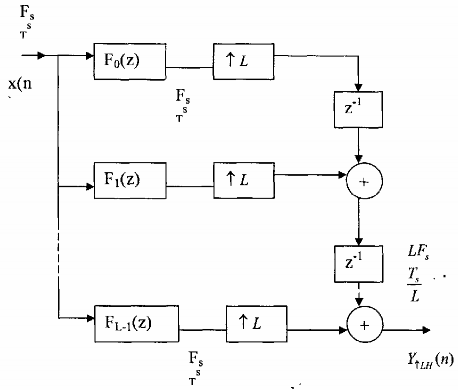
Hình 3.5.2.3
Ta thấy rằng tín hiệu vào xâu trước khi vào bộ lọc FIR đối với FIR LH trực tiếp,phải đi qua bộ nội suy L,chiều dài của xâu tăng lên L lần,và cứ L mẫu thì có L-1
mẫu giá trị không, khoảng thời gian giữa hai mẫu của yLH(n) bây giờ là Ts/L.
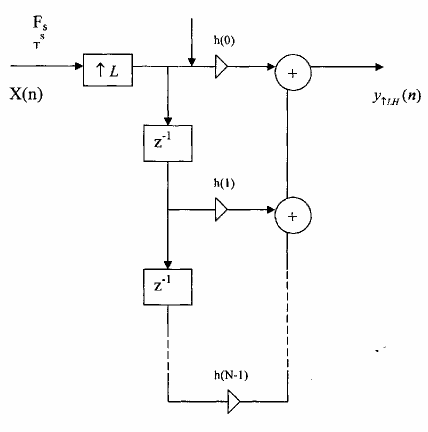
Hình 3.5.2.4
Hơn nữa chiều dài của bộ lọc FIR là N. Vậy để có một giá trị của yLH(n) trong thời gian Ts/L ta phải hoàn thành N phép nhân và N- 1 phép cộng. Như vậy ta không tận dụng được các nhân tố để giảm các tính toán yêu cầu trong một đơn vị thời gian.
Còn đối với FIR LH nhiều pha qua L thành phần thì xấu đi trực tiếp vào các khối lọc Fm(z) với chu kì lấy mẫu là Ts, và chiều dài của Fm(z) trung bình bây giờ là N/L. Vậy trong khoảng thời gian Ts ta chỉ hoàn thành số phép nhân và phép cộng trung bình N/L và N/L – 1.
Vậy rõ ràng là FIR LH nhiều pha L thành phần ưu việt hơn hẳn FIR LH trực tiếp
Ví dụ 3.5.2.1
Cho bộ lọc nội suy FIR 3H với h(n) như sau:
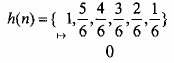
Giải:
Hãy vẽ cấu trúc nhiều pha tối ưu nhất của FIR 3H.
Ta tìm H(z) sau đó tìm E0(z3); E1(z3); E2(z3) rồi tìm F0(z3) = E2(z3) F1(z3) = E1(z3);
F2(z3) = E0(z3).
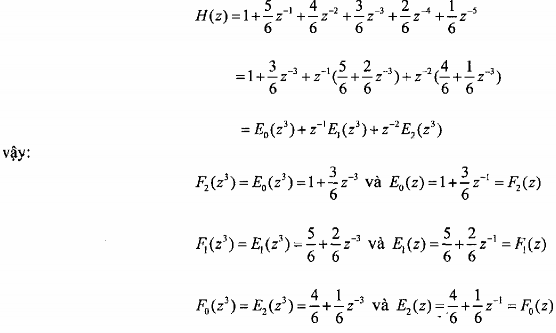
Từ đây ta có thể xây dựng cấu trúc nhiều pha 3 thành phần tối ưu nhất của IR.
3.5.3. Cấu trúc nhiều pha của các bộ lọc biến đổi nhịp hệ số M/L không nguyên
a) Tổng quan
Trên hình 3.3.3.3 chúng ta đã có sơ đồ khối của các bộ lọc biến đổi nhịp hệ số M/L với chỉ một bộ lọc số có đáp ứng xung h(n), đáp ứng tần số H(ej) van tần số cắt w =
min( π ,
L
π ). Nếu chúng ta tiến hành thực hiện bộ lọc biến đổi nhịp hệ số M/L HM/L
M
bằng cấu trúc trực tiếp của bộ lọc số hơn thì ta hoàn toàn không khai thác được nhân tố để làm giảm khối lượng tính toán đòi hỏi trong một thời gian và những phức tạp khác.Hình 3.5.3.2 minh họa bộ lọc biến đổi nhịp FIR có cấu trúc trực tiếp gọi tắt là FIR
HM/L trực tiếp.
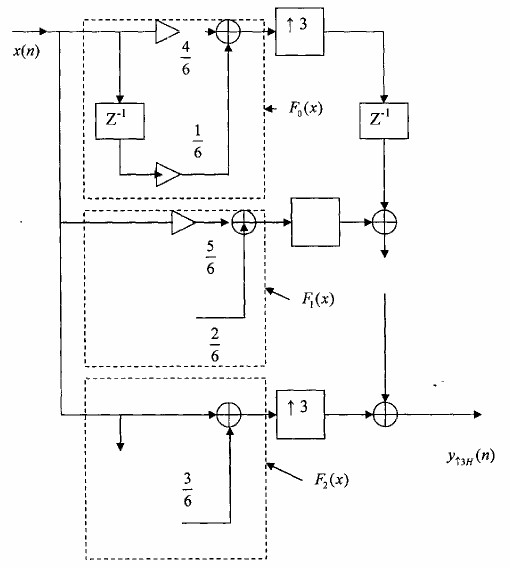
Hình 3.5.2.5
Để thu được sự thực hiện bộ lọc biến đổi nhịp H M/L ưu việt chúng ta sẽ dùng cấu trúc nhiều pha L hoặc M thành phần phụ thuộc vào ta dùng phân hoạch nhiều pha loại 1 hay loại 2.
b) Cấu trúc nhiều pha loại 1 của bộ óc biến đổi nhịp hệ số M/L không nguyên
Cấu trúc nhiều pha loại 1 của bộ lọc biến đổi nhịp hệ số M/L cho bởi hình Nhận xét:
- Cấu trúc trên hình 3.5.3.2 là cấu trúc nhiều pha loại 1 M thành phần của HM/L, gọi tắt là HM/L nhiều pha M thành phần.
- Cấu trúc nhiều pha loại này không nói lên được những ưu việt của cấu trúc nhiều pha, vì vậy chúng ta phải biến đổi sơ đồ này đi.
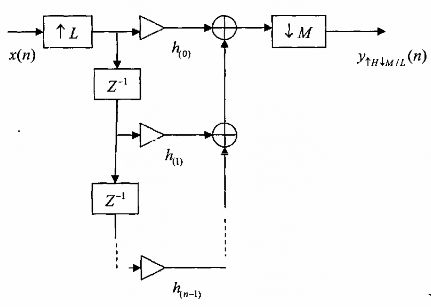
Hình 3.5.3.1
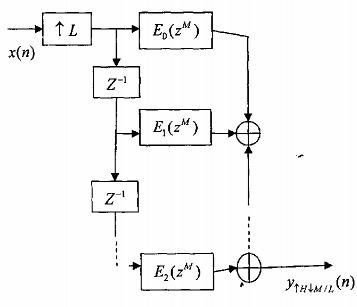
Hình 3.5.3.2
Áp tính phân phối vào phép công của phép phân chia và sử dụng sự đồng nhất của hai sơ đồ (a) và (b) trên hình 3.3.1.2 ta có thể chuyển cấu trúc trên hình 3.5.3.2 thành cấu trúc trên hình 3.5.3.3.