Cấu Trúc Nhiều Pha Của Bộ Lọc Lấy Mẫu

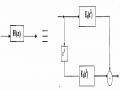
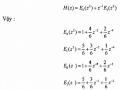Hình 3.5.3.7

(a) Cấu trúc thực hiện thủ tục z-1 = z-3z-2 và đưa bộ 3 vào 2 nhánh theo tính chất phân bố vào phép cộng của phép nội suy; (b) Cấu trúc thực hiện sự đồng nhất (3.3.2.11) và (3.3.1.11) tức là 3  zz-1 và z2  2 = 2z; c) Cấu trúc thực hiện sự tương đương (3.2.4.5) tức là 2/3 2/3.

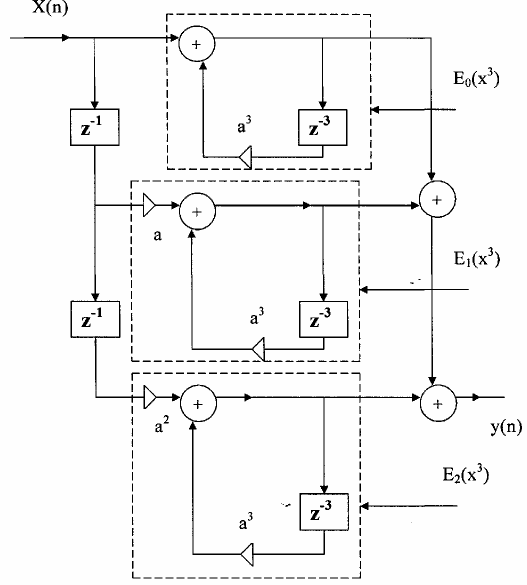
Đối với hình 3.5.3.7 (c) ta lại dùng phân hoạch nhiều pha loại 2 cho các thành phần nhiều pha E0(z) và E1(z) như sau:

E0(z) = z-2E00(z3) + z-1E01(z3) + E02(z3) E1(z) = z-2E10(z3) + z-1E11(z-3) + F12(z3)

Sau đó sử dụng sự đồng nhất (3.3.2.11) chúng ta sẽ có cấu trúc trên hình 3.5.3.8.

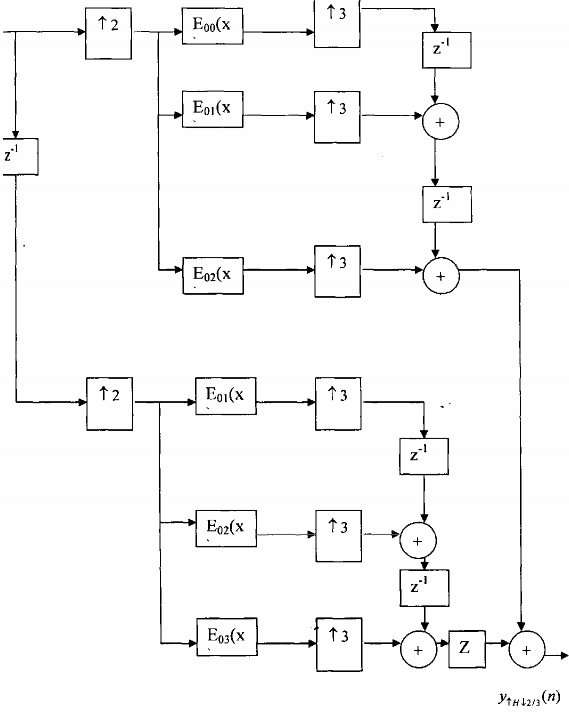
Hình 3.5.3.8

Có thể bạn quan tâm!

• Bộ Lọc Biến Đổi Nhịp Lấy Mẫu Với Hệ Số M L‌
• Phân Hoạch Nhiều Pha (Polyphase Decomposition)
• Xử lý tín hiệu số 2 Phần 2 - 7
• Cấu Trúc Nhiều Pha Của Các Bộ Lọc Biến Đổi Nhịp Hệ Số M/l Không Nguyên
• Một Vài Ứng Dụng Của Hệ Thống Lọc Số Nhiều Nhịp
• Xử lý tín hiệu số 2 Phần 2 - 11

Xem toàn bộ 140 trang tài liệu này.

Rõ ràng là cấu trúc trên hình 3.5.3.8 là cấu trúc ưu việt nhất, chúng ta không thể cải tiến thêm được nữa. Với cấu trúc này nhịp của tín hiệu vào x(n) trước khi vào các bộ lọc sẽ giảm đi 2 lần (tổng quát là M lần) tức là chu kỳ lấy mẫu tăng 2 lần: 2Ts. Nếu giả sử



N 1

h(n) là bộ lọc FI có chiều dài N = H(z) = h(n)z 1 thì các bộ lọc con E01(z) và E11(z) sẽ

n0

có chiều dài giảm đi 2 x 3 = 6 lần (tổng quát là M x L lần).

3.4.3. PHÂN HOẠCH NHIỀU PHA LOẠI HAI

a) Phân hoạch nhiều pha loại hai hàm H(z)

Trong mục nhỏ này chúng ta đưa khái niệm phân hoạch nhiều pha loại hai, trong một số trường hợp cách phân hoạch này sẽ thuận lợi hơn.

Từ biểu thức của phân hoạch nhiều pha loại 1 ta có:

Đổi biến số: 1 = M - 1 - m Ta có:

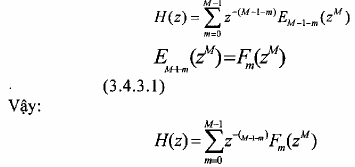
0 m M - 1 (3.4.3.2)

Biểu thức (3.4.3.2) là biểu diễn của H(z) dưới dạng phân hoạch nhiều pha M thành phần loại hai.

Nhận xét:

- Ta thấy rằng Fm(zM)  EM-1-m (zM) là biểu diễn của H(z) Fm(zM)  Em (zM) chỉ là việc đánh số lại các thành phần mà thôi.Vì vậy về mặt bản chất thì phân, hoạch nhiều pha loại 2 và loại 1 không có gì khác nhau,chúng chỉ khác nhau về mặt hình thức.

- Phân hoạch nhiều pha loại 2 rất có lợi khi thực hiện bộ lọc nội suy.

Ví dụ 3.4.3.1

Cho bộ lọc FIR pha tuyến tính, hàm H(z) có phân hoạch pha loại 1 như sau: H(z) = E0(z3) + z-1E1(z3) + z-2 E2(z3)

E0(z3) = 1 + 4z-3 + z-6

E1(z3) = 2 + 3z-3 E2(z3) = 3 + 2z-3

Hãy tìm phân hoạch nhiều pha loại 2 của H(z).

Giải:

Áp dụng hệ công thức (3.4.3.1) và (3.4.3.2) ta có:

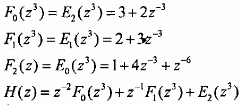
b) Cấu trúc nhiều pha loại 2:

trên cơ sở biểu thức (3.4.3.2) của phân hoạch nhiều pha loại 2 của hàm H(z):

Chúng ta xây dựng được sơ đồ cấu trúc nhiều pha loại 2 M thành phần xem hình 3.4.3.1.

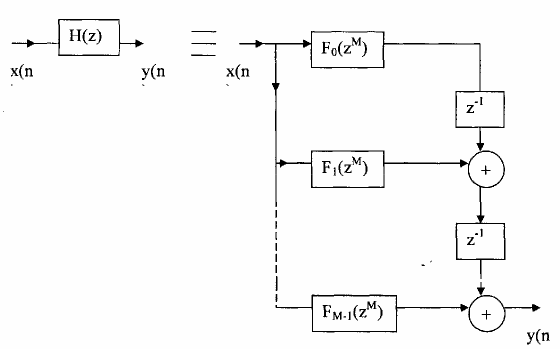
Hình 3.4.3.1

Nhận xét:

- Thực chất cấu trúc nhiều pha loại 2 chính là cấu trúc chuyển vị của cấu trúc nhiều pha loại nức là nếu ta coi cấu trúc loại 1 là một graphe có hướng,nếu ta đổi hướng giữa đầu vào va đầu ra, nút cộng sẽ thành nút phân tán, nút phân tán trở thành nút cộng thì hàm truyền đạt H(z) của cấu trúc sẽ không thay đổi, lúc đó ta sẽ thu được cấu trúc loại 2 gọi là cấu trúc chuyển vị.

- Cấu trúc nhiều pha loại 2 rất thuận lợi cho việc xây dựng bộ lọc nội suy

Hình 3.4.2.2‌‌

3.5. CẤU TRÚC NHIỀU PHA CỦA BỘ LỌC LẤY MẪU

3.5.1. Cấu trúc nhiều pha của bộ lọc phân chia

Từ hình 3.3.3.1 và hình 3.4.2.2 ta có thể thực hiện được bộ lọc phân chia nhiều pha như hình vẽ 3.5.1.1.

Nhận xét:

- Thực chất cấu trúc trên hình 3.5.1.1 này là dựa trên cơ sở cấu trúc hình 3.3.1.1 vì nó không nói lên được tính ưu việt của cấu trúc nhiều.

- Nói chung bộ lọc phân chia hệ số M sẽ dược thực hiện trên cơ sở sử dụng cấu trúc nhiều pha M thành phần,có như vậy ta sẽ lợi dụng sự đồng nhất của 2 sơ đồ (a) và (b) trên hình 3. 3.1.2.

- Vì phân chia có tính phân phối vào phép cộng nên ta có thể chuyển cấu trúc hình

3.5.1.1 thành cấu trúc 3.5.1.2 mà kết quả vẫn như nhau.

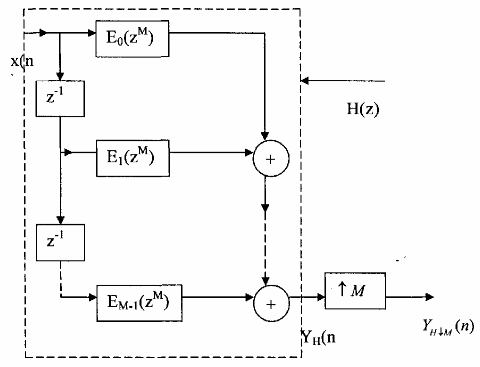
Hình 3.5.1.1

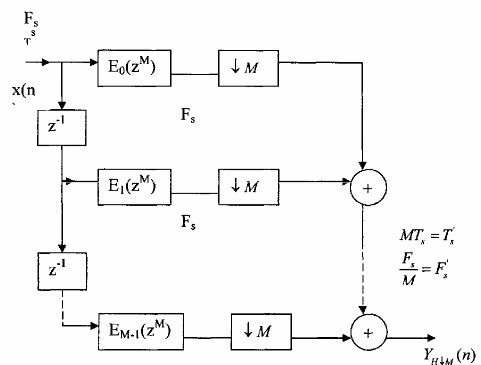
Hình 3.5.1.2

Sử dụng sự đồng nhất của sơ đồ (a) và (b) trên hình 3.3.1.2 ta có thể chuyển cấu trúc trên hình 3.5.1.2 thành cấu trúc trên hình 3.5.1.3.

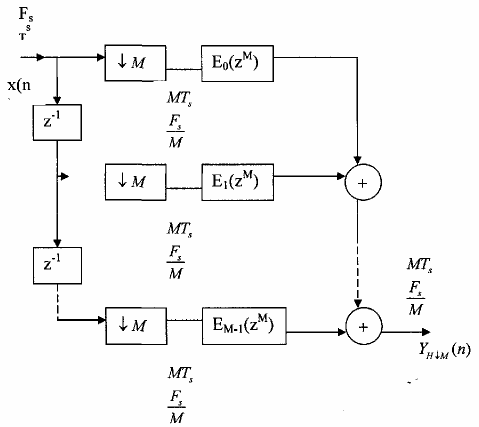
Hình 3.5.1.3

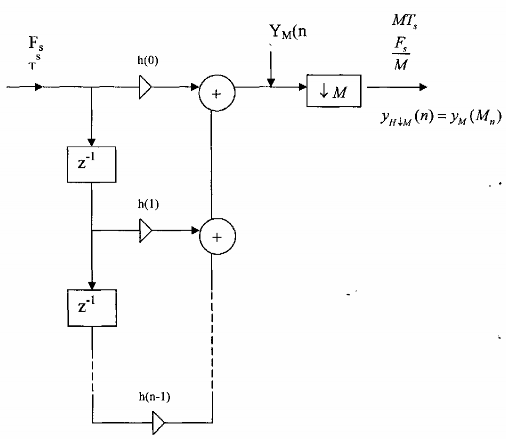
Cấu trúc trên hình 3.5.1.3 là cấu trúc ưu việt nhất, nó chính là cấu trúc nhiều pha M thành phần của bộ lọc phân chia hệ số M. Để thấy được ưu điểm của cấu trúc nhiều pha như trên hình chúng ta cũng so sanhb với cấu trúc trực tiếp của bộ lọc phân chia HÔM.Giả sử chúng ta đồng bộ lọc FIR có chiều dài N,cấu trúc trực tiếp của HÔM được cho trên hình 3.5.l.4. Ta viết tắt bộ lọc phân chia FIR là FIRHM.Bây giờ ta tiến hành so sánh.

Ta thấy rằng đối với FIR HM trực tiếp, để tính mỗi một đầu ra yHM(n) chúng ta cần N phép nhân và (N - 1) phép cộng. Trong sơ đồ hình 3.5.1.4 ta thấy rằng tín hiệu vào x(n) qua các bộ trễ z^- 1 rồi được nhân với hệ số h(n), sau đó cộng lại ta được một giá trị của yH(n). Còn trong thời gian thực (in real time) các bộ trễ z^- 1 chính là bộ ghi dịch, x(n) đi vào các bộ ghi dịch theo từng thời điểm của xung đồng bộ, ta gọi là xung nhịp, khoảng cách thời gian giữa 2 xung nhịp liên tiếp nhau là Ts. Vậy sau mỗi nhịp ta phải thực hiên xong N phép nhân van N- 1 phép cộng trước khi xung nhịp mới thực hiện, tức là FIR HM trực tiếp chỉ tính giá trị y(Mn) chứ không cần tính cả yH(n) ,vậy hệ thống sẽ nghỉ trong thời gian (M-1)Ts, sau đó bộ ghi dịch sẽ dịch một bước dài M nhịp để tính giá trị tiếp theo của yH(n) như vậy rõ ràng là rất bất tiện.

Hình 3.5.1.4

Còn đối với FIR HM nhiều pha M thành phần thì trước khi đi vào các khối lọc Em(z) thì các mẫu nằm giữa hai mẫu Mn và M(n +1) không còn nữa, tức là nhịp lấy mẫu đã được giảm đi M lần, thời khoảng giữa hai mẫu trước khi đi vào Em(z) bây giờ là MTS. Như vậy các phép tính nhân và cộng sẽ được thực hiện trong khoảng thời gian MTS. Hơn nữa chiều dài các bộ lọc Em(z) bây giờ là trung bình N/M vậy số phép nhân và cộng phải thực hiện trong khoảng thời khoảng MTS chỉ còn trung bình là N/M và N/M- 1.

Như vậy FIR HM nhiều pha M thành phần ưu việt hơn hẳn FIR HM trực tiếp.

Ví dụ 3.5.1.1:

Cho bộ lọc phân chia FIR FIR H2 với hầu như sau:

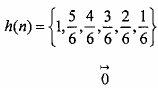
Giải

Hãy vẽ cấu trúc nhiều pha tối ưu nhất của FIR H2.

Ta tìm H(z) sau đó tìm E0(z) và E1(z):