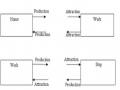
Hình 4.1 Quy trình, dự báo phân tích nhu cầu đi lại theo mô hình 4 bước
Quy trình bốn bước này sử dụng những mô hình toán học độc lập khác nhau cho mỗi hợp phần của quy trình. Kết quả của bước này thường là dữ liệu đầu vào để giải quyết các bước tiếp theo.
Sau đây trình bày từng bước cụ thể:
Bước 1. Phát sinh hành trình (Trip Generation)
Mô hình phát sinh hành trình dự báo và xác định số lượng lượt đi lại xuất phát trong vùng phân tích (mức độ tổng thể), lượt đi lại của hộ gia đình (mức độ cá thể) hoặc những nhóm tương đương.
Mục đích của bước này nhằm xác định số chuyến đi phát sinh của từng vùng trong khu vực nghiên cứu. Số chuyến đi của từng vùng phù thuộc vào đặc điểm sử dụng đất và các đặc điểm kinh tế xã hội của người sử dụng giao thông cũng như các yếu tố khác có liên quan đến giao thông vận tải.
Trip Generation: Phân loại theo lục đích chuyến đi gồm 2 loại chính là HB (Home Based) và NHB (Non_Home Based).
Trong HB phân theo những loại sau:
Có thể bạn quan tâm!
-
 Nhu Cầu Đi Lại Trong Khu Vực Nghiên Cứu Theo Mục Đích Và Phương Thức
Nhu Cầu Đi Lại Trong Khu Vực Nghiên Cứu Theo Mục Đích Và Phương Thức -
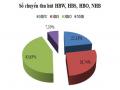
 Tỷ Lệ Đảm Nhận Phương Thức Theo Mục Đích Chuyến Đi Hbw, Hbs, Hbo, Nhb
Tỷ Lệ Đảm Nhận Phương Thức Theo Mục Đích Chuyến Đi Hbw, Hbs, Hbo, Nhb -
 Mô Hình Dự Báo Nhu Cầu Giao Thông 4 Bước
Mô Hình Dự Báo Nhu Cầu Giao Thông 4 Bước -
 Các Dự Án, Nghiên Cứu Áp Dụng Phần Mềm Cube Citilabs Ở Việt Nam.
Các Dự Án, Nghiên Cứu Áp Dụng Phần Mềm Cube Citilabs Ở Việt Nam. -
 Xây Dựng Mạng Lưới Đường Ngoại Vùng (Đường Kết Nối)
Xây Dựng Mạng Lưới Đường Ngoại Vùng (Đường Kết Nối) -
 I (Internal – Internal) Là Chuyến Đi Nội Vùng, Điểm Đi Và Điểm Đến Của Hành Trình Đều Nằm Trong Nội Vùng Khảo Sát.
I (Internal – Internal) Là Chuyến Đi Nội Vùng, Điểm Đi Và Điểm Đến Của Hành Trình Đều Nằm Trong Nội Vùng Khảo Sát.
Xem toàn bộ 172 trang tài liệu này.
Chuyến đi công việc ( giữa Nhà và Nơi làm việc)
Chuyến đi nhà và trường học ( bao gồm cả trường Đại học, Cao đẳng,..)
Mua sắm
Xã hội và giải trí
Chuyến đi đưa đón
Chuyến đi khác
Với 2 chuyến đi đầu ( Chuyến đi với mục đích công việc giữa Nhà và Nơi làm việc, chuyến đi giữa Nhà và Trường học) là chuyến đi bắt buộc trong phân tích chuyến đi. Chuyến đi cuối cùng (Chuyến đi khác) ít được lựa chọn hơn: đi bệnh viện, đi khám bệnh, chuyến đi làm nhưng không đến nơi làm việc. Tùy thuộc vào đặc điểm của khu vực, văn hóa và xã hội có thể ảnh hưởng đến việc phân chia chuyến đi.
Chuyến đi NHB có thể chia bằng hai loại chính: đi công việc và khác. Đi công việc từ công ty đến công ty. Các chuyến đi này đều không liên quan đến Nhà.
Các yếu tố ảnh hưởng đến phát sinh chuyến đi:
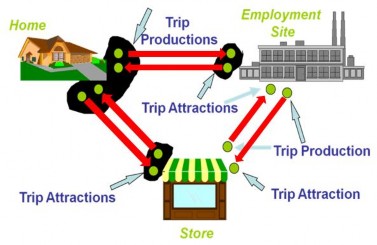
Phát sinh chuyến đi cá nhân (Productions): Những yếu tố chính ảnh hưởng đến phát sinh chuyến đi như:
Sở hữu xe ôtô và xe máy
Quy mô hộ gia đình
Kích cở hộ gia đình
Tính chất khu vực(KCN,KDC…)
Mật độ cư trú
Khả năng tiếp cận
Với 4 yếu tố đầu đã được xem xét, nghiên cứu trong các nghiên cứu về phát sinh chuyến đi hộ gia đình, trong khi các yếu tố khác liên quan đến các nghiên cứu phát sinh chuyến đi của khu vực, yếu tố cuối ít được dùng.
Thu hút chuyến đi cá nhân ( Attractions)
Yếu tố liên quan, quan trọng nhất là diện tích các KCN, khu vui chơi…Ngoài ra còn 1 số yếu tố khác cũng ảnh hưởng.
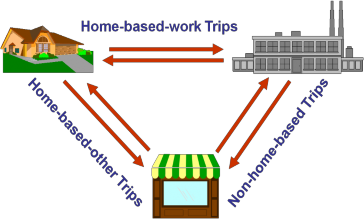
Hình 4.2 Định nghĩa chuyến đi theo mục đích
Nguồn: Tài liệu hướng dẫn Cube của Citilabs.
Hình 4.3 Phát sinh và hấp dẫn hành trình
Hai phương pháp truyền thống là phân tích phân loại chéo và phân tích hồi quy. Trong đồ án này sử dụng phương pháp hồi quy để tính toán.
Phương pháp phân tích hồi qui (Regression analysis):
Phân tích hồi qui là phương pháp thống kê mà giá trị trung bình (mean) của một hay nhiều biến ngẫu nhiên là được dự đoán dựa vào điều kiện của các biến ngẫu nhiên (đã tính toán) khác. Cụ thể, có hồi qui tuyến tình, hồi qui lôgic, hồi qui Poisson và học có giám sát. Phân tích hồi qui không chỉ là trùng khớp đường cong (lựa chọn một đường cong mà vừa khớp nhất với một tập điểm dữ liệu); nó còn phải trùng khớp với một mô hình với các thành phần ngẫu nhiên và xác định (deterministic and stochastic components). Thành phần xác định được gọi là bộ dự đoán (predictor) và thành phần ngẫu nhiên được gọi là phần sai số (error term).
Một hàm hồi quy tổng quát như sau:
Yi = ai + β1X1 + β2X2 + … + βnXn + εi Trong đó:
- Yi = là số hành trình phát sinh ra trong vùng i.
- ai = số thực.
- β1…. βn: = hệ số hồi quy.
- X1…Xn = biến số ngẫu nhiên (các biến số đại diện cho một yếu tố ảnh hưởng đến số lượt đi lại ví dụ như dân số, hộ gia đình…
- εi = hệ số hiệu chỉnh (số dư).
Các giá trị ao, β1, β2,… βk, εi được xác định bằng phương pháp hồi quy.
Bước 2. Phân phối hành trình (Trip distribution)
Sau khi dự báo được nhu cầu đi lại phát sinh ra trong vùng phân tích, mục tiêu tiếp theo là phải xác định được những hành trình này đi đâu trong số các hành trình xuất phát từ một điểm đi và đến nhiều điểm đến.
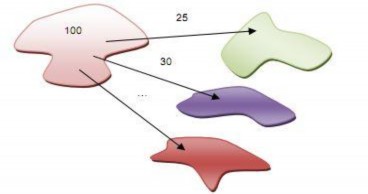
Hình 4.4 Sự phân phối hành trình
Có ba yếu ảnh hưởng tới sự phân chia này:
+ Số lượng hành trình phát sinh từ điểm xuất phát.
+ Sự hấp dẫn của vùng đến.
+ Trở kháng (Chi phí, thời gian đi lại).
Phương pháp thông dụng để xác định sự phân phối hành trình là dùng mô hình phân phối hấp dẫn (Gravity mode), phương pháp này xác định rò số hành trình đi lại giữa điểm xuất phát và điểm đến như là một hàm số về thuộc tính đi và đến (thuộc tính OD) và chi phí đi lại giữa chúng:
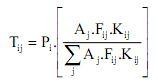
Trong đó:
Tij = Hành trình từ vùng i đến vùng j.
Pi = Tổng số hành trình phát sinh từ vùng i. Aj = Số hành trình hấp thu vào vùng j.
Fij = Hệ số trở kháng, thông thường là hàm số tỷ lệ nghịch với thời gian di chuyển giữa i và j.
Kij = Hệ số hiệu chỉnh về mặt kinh tế xã hội cho những hành trình xuất phát từ i và đến vùng j, thường lấy bằng 1.
Ta đã biết Ps và As được xác định được từ quá trình phát sinh hành trình, tổng hành trình phát sinh ra phải bằng tổng hành trình hấp thu.
ΣPi = ΣAj.
Khi tổng số hành trình hấp thu cho mỗi vùng không bằng tổng số hành trình hấp thu ban đầu, ta cần điều chỉnh lại nhân tố hấp thu. Ta phải tính toán lại nhân tố hấp thu theo công thức sau:
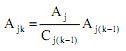
Trong đó:
- Ajk = Nhân tố hấp thu hiệu chỉnh cho vùng hấp thu (cột) j lần thứ k.
- Ajk = Aj khi k=1
- Cjk = Tổng giá trị hấp thu (cột) thực tế cho vùng j lần thứ k
- Aj = tổng số hấp thu mong muốn thuộc vùng hấp thu (cột) j
- j = số thứ tự khu vực hấp thu
- n = số lượng khu vực
- k = số lần lặp
Bước 3. Phân chia phương thức
Sau khi hoàn thành công tác phân phối hành trình, công việc tiếp theo là phải xác định được phương thức đi lại bằng phương tiện nào sẽ được sử dụng. Giai đoạn
này dự báo có bao nhiêu người sử dụng phương tiện giao thông công cộng và bao nhiêu người sử dụng phương tiện giao thông cá nhân. Ở bước này mô hình sử dụng lý thuyết lựa chọn rời rạc cho trường hợp nhiều lựa chọn hoặc lựa chọn Binary (mô hình nhị phân) cho trường hợp có 2 lựa chọn.
Phương pháp thông thường nhất được sử dụng là mô hình Logit.
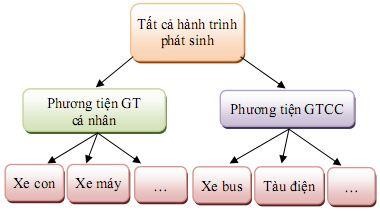
Hình 4.4 Phân chia phương thức
Ở bước thứ 3 của dự báo nhu cầu giao thông sử dụng mô hình lựa chọn logit để tính toán. Trong Cube, mô hình đơn giản nhất được sử dụng là mô hình logit tuyệt đối.
Mô hình lựa chọn đơn giản này chia tổng nhu cầu đi lại giữa hai lựa chọn thay thế, nó được gọi là mô hình Binary. Điều này có thể được mở rộng bằng cách thêm các phương thức khác, do đó tạo thành một mô hình đa thức.
Đây là một ví dụ đơn giản của mô hình tổng cầu. Giả sử rằng trong một hệ thống giao thông chỉ có hai phương thức rời rạc cạnh tranh là Phương tiện cá nhân (Car) và giao thông công cộng (PT) - giữa một tập hợp các điểm đi và điểm đến. Người sử dụng một hệ thống như vậy được gọi là sự lựa chọn nhị phân, bởi vì chỉ có hai lựa chọn thay thế ( Cá nhân hoặc PT).
Phương tiện GTCC
Tất cả hành trình
Phương tiện cá nhân
Quá trình này bắt đầu bằng cách tính toán chi phí tổng quát giữa địa điểm đi và địa điểm đến bằng các phương thức. Thông thường, chi phí này là sự kết hợp tuyến tính của các chi phí tiền tệ (giá vé, nhiên liệu, vv) và thời gian (đi bộ, chờ đợi, trung chuyển, thời gian trong xe, vv). Cũng có thể sử dụng một hằng số phụ gần đúng nào đó của các yếu tố chi phí để có thể dễ dàng xác định được số lượng, ví dụ như sự tiện lợi của dịch vụ xe buýt, hoặc chất lượng xe chạy trên đường. Gọi chi phí đi lại bằng Phương tiện cá nhân là CCar và PT là Cpt. Giả sử rằng có một nhu cầu tổng là D và cuộc hành trình trong một thời gian nhất định. Theo mô hình Logit tuyệt đối thì xác suất của việc lựa chọn Phương tiện cá nhân (PCar )và PT (PPT ) được đưa ra bởi các phương trình dưới đây:
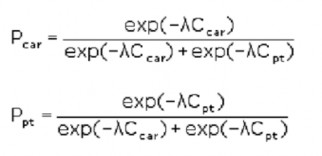
Với λ là tham số quy mô.
Các dự báo nhu cầu xe cá nhân ( Dcar )và PT ( Dpt ) là:
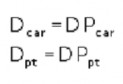
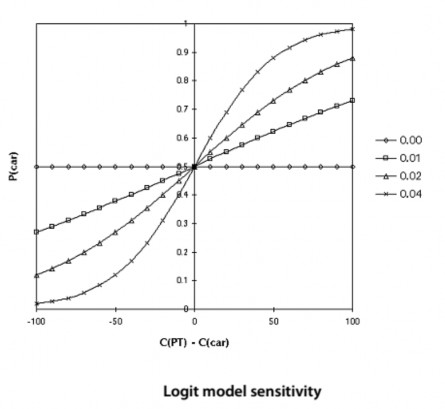
Các trường hợp của mô hình được xác định bởi một hằng số dương như tham số quy mô, được gọi là λ trong các phương trình trên. Biểu đồ dưới đây cho thấy sự nhạy của mô hình với các giá trị khác nhau của λ.
Nếu λ = 0 mô hình này là hoàn toàn không nhạy với chi phí và nhu cầu được chia đều giữa mỗi lựa chọn có sẵn. Chú ý rằng Pcar = 1/2 và Ppt = 1/2 khi λ = 0. Khi λ tăng, độ nhạy của mô hình logit này tăng theo, dần dần phân bổ nhu cầu nhiều hơn để lựa chọn với chi phí thấp hơn. Con số "mô hình logit nhạy" cho thấy mô hình trở nên nhạy hơn với sự khác biệt về chi phí khi λ = 0,01, 0,02 và 0,04.
Cuối cùng, khi λ tiến tới vô cùng, mô hình sẽ phân bổ tất cả các nhu cầu thay thế với chi phí thấp nhất. Giá trị của tham số quy mô sẽ phụ thuộc vào bản chất của sự lựa chọn, đặc trưng nhu cầu các đơn vị chi phí. Ví dụ:
Nguồn: Tài liệu hướng dẫn sử dụng CUBE của Citilabs
Hình 4.5 Độ nhạy mô hình Logit
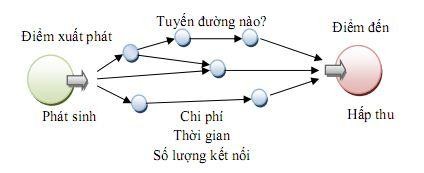
Bước 4. Ấn định tuyến đường (Traffic assignment)
Đây là giai đoạn cuối cùng sau khi xác định phương thức phân chia, mục đích là phải xác định được tuyến đường nào (cho mỗi phương thức) được sử dụng cho những hành trình từ điểm đi đến điểm đến.
Hình 4.6 Tuyến đường nào sẽ được lựa chọn cho hành trình?