CHƯƠNG 3: THIẾT KẾ.
Trong chương 4 này sẽ trình bày việc thiết kế từng khối và ghép các khối thành hệ thống truyền thông MIMO hoàn chỉnh. Để tiện theo dõi, việc thiết kế sẽ được phân tích theo từng khối chức năng ở cả bên phát và bên thu. Ngoài ra, đề tài còn trình bày quy trình chung để thiết kế hệ thống trên phần cứng FPGA.
3.1 Mô hình thiết kế.
3.1.1 Sơ đồ khối.
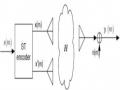
Mô hình hệ thống MIMO được thiết kế như hình 3.1.
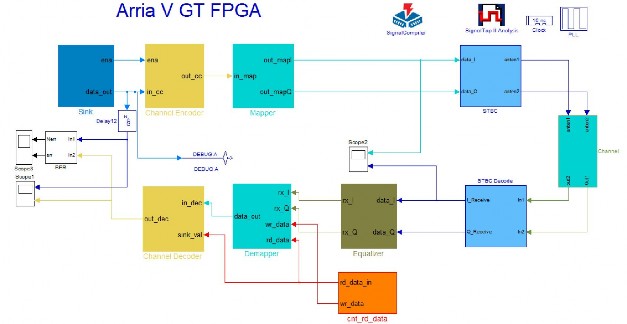
Hình 3.1. Mô hình thiết kế hệ thống MIMO-STBC
3.1.2 Bộ tạo dữ liệu và các tín hiệu điều khiển.
Việc tạo dữ liệu để kiểm tra khả năng hoạt động của mạch được thực hiện bằng cách đặt dữ liệu trong một bảng tra, như vậy, dữ liệu ta có thể kiểm soát được. Bảng dữ liệu tạo sẵn 320 giá trị nhằm tiện cho việc mở rộng hệ thống MIMO-OFDM sau này. Hệ thống OFDM có 320 kênh con, trong đó có 64 Cyclic Prefix, 55 giá trị ‘0’ ở hai đầu của symbol, một giá trị ‘0’ ở chính giữa, và 8 kênh con dùng cho pilot. Vì
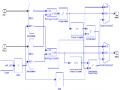
vậy, chỉ có 192 kênh còn lại được dùng cho dữ liệu. Đề tài sử dụng bộ mã hoá convolution code ½. Trong trường hợp phép đều chế QPSK, ta có mỗi symbol sẽ mang 2 bit thông tin. Vì vậy, một symbol của hệ thống sẽ mang được 192 bit thông tin. Do đó, ta sẽ đặt 192 giá trị nhị phân vào bảng tra và 192 giá trị ‘0’ tức là không có thông tin để đảm bảo thời gian chèn bit và symbol OFDM. Bộ đếm có nhiệm vụ truy xuất giá trị trong bảng tra và thực hiện chức năng làm chỉ số symbol (index_out) cho cả hệ thống. Tín hiệu data_out là dữ liệu được tạo. Tín hiệu cho phép (ena) dùng để báo hiệu cho các mạch ngẫu nhiên hoá, mã hoá kênh hoạt động. Hình 3.2 thể hiện mạch tạo dữ liệu và các tín hiệu điều khiển.
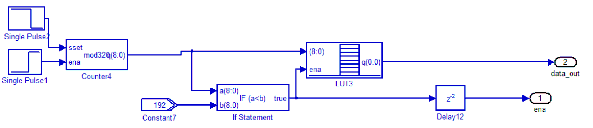
Hình 3.2. Mạch tạo dữ liệu và tín hiệu điều khiển.
3.1.3 Bộ mã hóa.
Bộ mã hoá kênh được sử dụng là bộ mã convolutional code, tốc độ mặc định là 1/2, chiều dài bộ mã hoá là 7 và dùng đa thức sinh là: G1 = 171OCT và G2 = 133OCT. Bộ mã hoá được thiết kế bằng cách kết hợp 6 bộ trễ (delay) và 2 cổng XOR 5 ngõ vào. Hình 3.3 trình bày bộ mã hóa Convolutional Code. Cổng in_cc là ngõ vào của bộ mã hóa, cổng out_cc là ngõ ra của bộ mã hóa. Tín hiệu sau khi qua 2 bộ XOR tương ứng với G1 và G2 của mã hóa. Ena là tín hiệu cho phép mã hóa.
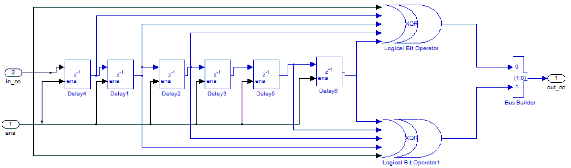
Hình 3.3. Bộ mã hóa Convolutional code
3.1.4 Bộ giải mã bằng thuật toán Viterbi.
Đề tài sử dụng bộ giải mã bằng thuật toán Viterbi. Kiến trúc căn bản của thuật toán Viterbi được trình bày trong hình 3.4. Thuật toán gồm bốn khối chính: khối tính khoảng cách nhánh (branch metric), khối cộng-so sánh-chọn (add compare and select), khối chọn đường tối ưu (survivor path metric), và khối quy hồi và giả mã (traceback and output decode block).
Khối tính khoảng cách nhánh (branch metric) dùng đểtính khoảng cách Hamming của các bit (là 2 bit nếu sử dụng tốc độ mã là R=1/2) với các nhánh. Khối cộng-so sánh-chọn có nhiệm vụ tính tổng khoảng cách Hamming của nhánh với trạng thái hiện tại và giữ lại nhánh có khoảng cách ngắn nhất. Khối chọn đường tối ưu để tìm ra chuỗi trạng thái phù hợp nhất. Khối quy hồi và giả mã có nhiệm vụ chọn, dò lại chuỗi trạng thái tối ưu và quyết định chuỗi bit ở ngõ ra. Đây là chuỗi bit giải mã của thuật toán.
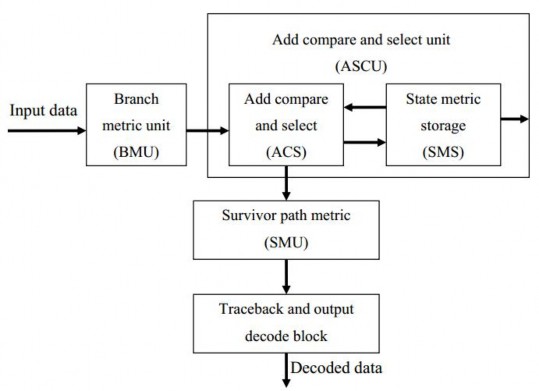
Hình 3.4. Mô hình thuật toán Viterbi
Hình 3.5 là ví dụ về giải mã dùng thuật toán Viterbi cho chuỗi dữ liệu thu là (11, 00, 01, 11, 10, 10, 11). Chuỗi trạng thái phù hợp nhất được xác định bằng cách tính khoảng cách Hamming với tất cả các đường. Khi hai đường cùng gặp nhau tại một điểm, ta chỉ giữ lại đường có khoảng cách Hamming ngắn hơn. Đường cuối cùng được chọn để quyết định trạng thái ngõ ra là đường có khoảng cách Hamming ngắn nhất. Vì vậy, chuỗi dữ liệu tối ưu nhất là (11, 01, 01, 11, 11, 10,11). Khi xác định được chuỗi dữ liệu tối ưu, ta có thể xác định chuỗi dữ liệu ở ngõ ra bộ giải mã. Trong ví dụ trên, chuỗi dữ liệu sau khi giải mã là (1100100).
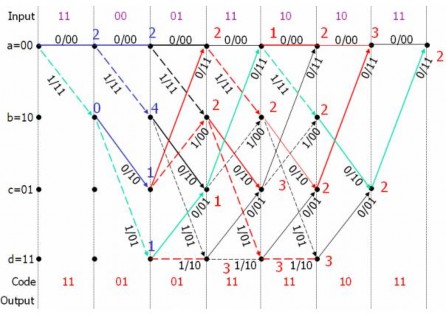
Hình 3.5. Ví dụ giải mã dùng thuật toán Viterbi
Đề tài sử dụng MegaCore để thực hiện bộ giải mã dùng thuật toán Viterbi.
Khối chức năng được thể hiện trong hình 3.6.
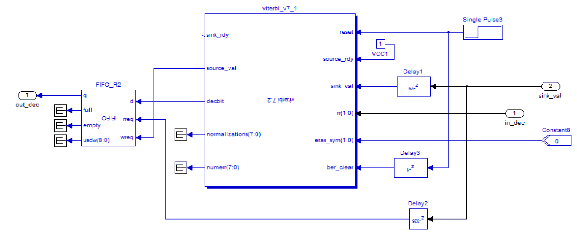
Hình 3.6. Bộ giải mã dùng thuật toán Viterbi.
Các đường tín hiệu cơ bản để điều khiển bộ giải mã được trình bày ở hình 3.7. Thuật toán Viterbi dựa vào chuỗi trạng thái phù hợp nhất. Vì vậy, việc xác định độ dài của chuỗi sẽ ảnh hưởng đến hiệu quả của bộ giải mã. Nếu chiều dài được chọn quá dài sẽ làm cho tăng các phép tính toán, sử dụng nhiều bộ nhớ, và tăng thời gian trễ. Ngược lại, nếu chọn chiều dài quá ngắn sẽ hạn chế khả năng sửa lỗi của thuật toán. Chiều dài qui hồi thường được chọn gấp 6 lần chiều dài bộ mã trong trường hợp không bỏ bớt. Trong trường hợp có bỏ bớt, chiều dài được chọn tối đa dài gấp 15 lần chiều dài bộ mã. Trong thiết kế này, chiều dài bộ mã là 7 và không sử dụng kỹ thuật bỏ bớt nên chiều dài qui hồi được chọn là 42. Chi tiết các đường tín hiệu được diễn tả ở
Bảng 3-1. Các dữ liệu đến bộ giả mã là không liên tục nên dữ liệu ngõ ra của bộ giả mã là không liên tục. Các dữ liệu này sẽ được ghi vào bộ nhớ FIFO. Sau đó, tín hiệu rd_data_out sẽ đọc liên tục 192 bit dữ liệu trong bộ nhớ.
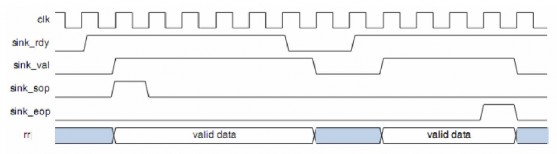
Hình 3.7. Dạng sóng của các tín hiệu điều khiển của khối giải mã Viterbi.
Bảng 3-1. Ý nghĩa các đường tín hiệu của bộ giải mã Viterbi
Hướng | Mô tả | |
sink_val | Input | Tín hiệu cho phép truyền dữ liệu |
rr | Input | Ngõ vào của dữ liệu cần giải mã. |
eras_sym | Input | Ngõ này sử dụng cho kỹ thuật bỏ bớt |
source_rdy | Input | Tín hiệu cho phép truyền dữ liệu ngõ ra |
ber_clear | Input | Xóa bộ đếm BER |
source_val | Output | Báo tín hiệu ngõ ra |
decbit | Output | Ngõ ra của tín hiệu sau giải mã |
sink_rdy | Output | Cho phép truyền dữ liệu ngõ vào |
normalizations | Output | Chứa các giá trị chuẩn hóa, đây là thông tin được dùng để tránh hiện tượng tràn bộ đếm. |
numerr | Output | Số bít lỗi Khởi động lại bộ giải mã. |
reset | Input | |
state_node_sync | Input | Sử dụng trong các trường hợp đặc biệt, dùng để thiết lập điểm bắt đầu của dữ liệu vào. |
Có thể bạn quan tâm!
-
 Hệ Thống Alamouti Stbc 2X1 Tại Khe Thời Gian Thứ Nhất Tín Hiệu Nhận Được Có Dạng:
Hệ Thống Alamouti Stbc 2X1 Tại Khe Thời Gian Thứ Nhất Tín Hiệu Nhận Được Có Dạng: -
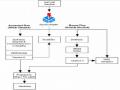
 Quy Trình Thiết Kế Của Dsp Builder
Quy Trình Thiết Kế Của Dsp Builder -
 Sơ Đồ Kết Nối Anten. Các Đặc Tính Của Anten Được Mô Tả Trong Bảng Sau:
Sơ Đồ Kết Nối Anten. Các Đặc Tính Của Anten Được Mô Tả Trong Bảng Sau: -
 Mạch Thực Hiện Điều Chế Mimo-Stbc.
Mạch Thực Hiện Điều Chế Mimo-Stbc. -
 Thực hiện hệ thống MIMO STBC trên Board FPGA Arria V - 9
Thực hiện hệ thống MIMO STBC trên Board FPGA Arria V - 9 -
 Thực hiện hệ thống MIMO STBC trên Board FPGA Arria V - 10
Thực hiện hệ thống MIMO STBC trên Board FPGA Arria V - 10
Xem toàn bộ 87 trang tài liệu này.
3.1.5 Ánh xạ chòm sao.
3.1.5.1 Bộ ánh xạ chòm sao.
Ánh xạ chòm sao là phương pháp chuyển chuỗi dữ liệu có m bit thành một điểm a+jb dạng số phức. Trong đó, số bit m phụ thuộc vào phép ánh xạ. Đề tài sử dụng kiểu điều chế QPSK với m = 2. Có các phương pháp để thiết kế bộ mapper như sử dụng cấu trúc case hoặc dùng một bảng tra (LUT) hoặc dùng bộ nhớ ROM. Ở đây, khối mapper được thiết kế bằng bảng tra.
Hình 3.8 trình bày nguyên tắc của phép QPSK. Có hai bảng tra riêng được sử dụng để lưu giá trị trục đồng pha (I) và trục vuông pha (Q). Dữ liệu cần thực hiện ánh xạ sẽ đặt vào đường địa chỉ của bảng tra. Nội dung trong bảng tra lưu trữ giá trị
tương ứng với chòm sao. Dữ liệu được ánh xạ sẽ có giá trị từ -1 đến 1. Ngõ ra của bộ DAC là 14 bit. Vì vậy, đề tài chuẩn hoá tín hiệu về dạng số có dấu chấm cố định.
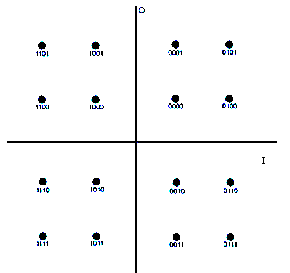
Hình 3.8. Giản đồ chòm sao phép điều chế QPSK và 16 QAM
Bảng 3-2 là các dữ liệu đặt trong bảng tra cho bộ mã hoá QPSK. Sơ đồ mạch thực hiện phép điều chế QPSK được trình bày ở hình 3.9.
Bảng 3-2. Dữ liệu bảng tra của QPSK
Ngõ ra | |||||
Hệ thập phân | Hệ nhị phân | Trục I | Trục Q | ||
Giá trị (hệ 10) | Số dấu chấm cố định (hệ 10) | Giá trị (hệ 10) | Số dấu chấm cố định (hệ 10) | ||
0 | 00 | 0.707 | 5792 | 0.707 | 5792 |
1 | 01 | 0.707 | 5792 | -0.707 | 10592 |
2 | 10 | -0.707 | 10592 | 0.707 | 5792 |
3 | 11 | -0.707 | 10592 | -0.707 | 10592 |
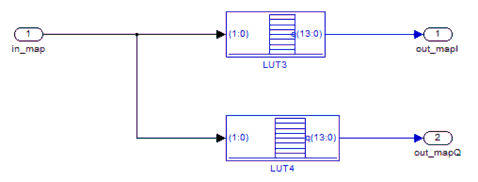
Hình 3.9. Mạch thực hiện phép điều chế QPSK.
3.1.5.2 Bộ giải ánh xạ chòm sao.
Ở đầu thu, các điểm chòm sao ở bộ truyền sẽ bị thay đổi do tác động của kênh truyền. Vì vậy, bộ giải ánh xạ chòm sao phải chọn ngưỡng để xác định điểm chòm sao ở phía thu. Khối giải ánh xạ chòm sao (demapper) được thiết kế bằng ngôn ngữ Verilog. Nguyên tắc của của bộ demapper là so sánh giá trị nhận được trên đường I và Q với các điểm lân cận trong chòm sao. Điểm được chọn ở ngõ ra là điểm có gần nhất với tín hiệu nhận được. Khi sử dụng phép QPSK, bộ demapper được thực hiện đơn giản bằng cách cho giá trị ngõ ra là bit có ý nghĩa lớn nhất (MSB) của chuỗi bit nhận được. Đây là bit dấu của chuỗi dữ liệu. Dữ liệu ở ngõ ra sẽ được đặt vào bộ nhớ FIFO để chuẩn bị đi vào bộ giải mã kênh. Ở đây dữ liệu truyền có 192 giá trị do đó bộ nhớ FIFO cần 192 từ nhớ. Mỗi từ có 2 bit nhớ tương ứng với phép điều chế QPSK. Hình 3.10 là mạch thực hiện demapper.
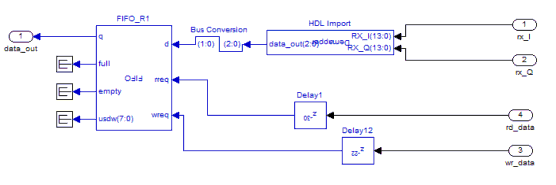
Hình 3.10. Bộ mapper và bộ nhớ FIFO