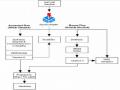
Tùy thuộc vào việc sử dụng nhiều anten hoặc ở nơi phát hoặc nơi thu mà người ta chia phân tập không gian thành ba loại:
Phân tập anten phát (hệ thống MISO) Phân tập anten thu (hệ thống SIMO)
Phân tập anten phát và thu (hệ thống MIMO).
2.1.3 Độ lợi trong hệ thống MIMO.
2.1.3.1 Độ lợi Beamforming.
Beamforming giúp hệ thống tập trung năng lượng bức xạ theo hướng mong muốn giúp tăng hiệu quả công suất, giảm can nhiễu và tránh được can nhiễu tới từ các hướng không mong muốn, từ đó giúp cải thiện chất lượng kênh truyền và tăng độ bao phủ của hệ thống. Để có thể thực hiện Beamforming, khoảng cách giữa các anten
Có thể bạn quan tâm!
-
Thực hiện hệ thống MIMO STBC trên Board FPGA Arria V - 1 -
Thực hiện hệ thống MIMO STBC trên Board FPGA Arria V - 2 -
Lý Thuyết Và Công Cụ Thiết Kế -
Quy Trình Thiết Kế Của Dsp Builder -
Sơ Đồ Kết Nối Anten. Các Đặc Tính Của Anten Được Mô Tả Trong Bảng Sau: -
Dạng Sóng Của Các Tín Hiệu Điều Khiển Của Khối Giải Mã Viterbi.
Xem toàn bộ 87 trang tài liệu này.
trong hệ thống MIMO thường nhỏ hơn bước sóng
(thông thường là
/ 2 ),
Beamforming thường được thực hiện trong môi trường ít tán xạ .Khi môi trường tán xạ mạnh hệ thống MIMO có thể cung cấp độ lợi ghép kênh không gian và độ lợi phân tập.
Hình 2.2. Kỹ thuật Beamforming.
2.1.3.2 Độ lợi ghép kênh không gian.
Hình 2.3. Ghép kênh không gian giúp tăng tốc độ truyền.
Tận dụng các kênh truyền song song có được từ đa anten tại phía phát và phía thu trong hệ thống MIMO, các tín hiệu sẽ được phát độc lập và đồng thời ra các anten (hình 2.3), nhằm tăng dung lượng kênh truyền mà không cần tăng công suất phát hay tăng băng thông hệ thống. Dung lượng hệ thống sẽ tăng tuyến tính theo số các kênh truyền song song trong hệ thống. Để cực đại độ lợi ghép kênh qua đó cực đại dung lượng kênh truyền thuật toán V-BLAST (Vertical- Bell Laboratories Layered Space- Time) được áp dụng.
2.1.3.3 Độ lợi phân tập.
Hình 2.4. Phân tập không gian cải thiện SNR.
Trong truyền dẫn vô tuyến, mức tín hiệu luôn thay đổi, bị Fading liên tục theo không gian, thời gian và tần số, khiến cho tín hiệu tại nơi thu không ổn định, việc phân tập cung cấp cho các bộ thu các bản sao tín hiệu giống nhau qua các kênh truyền Fading khác nhau (hinh 2.4), bộ thu có thể lựa chọn hay kết hợp hay kết hợp các bản sao tín hiệu này để giảm thiểu tốc độ sai bit BER, chống Fading qua đó tăng độ tin cậy của hệ thống. Để cực đại độ lợi phân tập, giảm BER và chống lại Fading, thuật toán STBC (Space-Time Block Code) và STTC (Space-Time Trellis Code) được áp dụng.
Thực tế, để hệ thống có dung lượng cao, BER thấp, chống được Fading, ta phải có sự tương quan giữa độ lợi phân tập và độ lợi ghép kênh trong việc thiết kế hệ thống.
2.1.4 MIMO Alamounti STBC.
Trong các hệ thống SISO, với một chuỗi thông tin {x1,x2,x3,…,xn} cần truyền, thông tin sẽ được truyền nối tiếp nhau, x1 rồi đến x2 ,… xn. Tuy nhiên, trong MIMO STBC không làm như thế, chuỗi thông tin cần truyền sẽ được sao ra vài bản tùy thuộc
vào số anten truyền, một bản sao tín hiệu tương ứng với 1 anten, được truyền vào không gian tại các thời điểm khác nhau dựa trên các anten khác nhau. Vì thế phương pháp này được gọi là kỹ thuật mã hóa khối không gian- thời gian (space-time block coding).
Mô hình của alamouti là mô hình STBC đầu tiên được nhà khoa học Siavash M Alamouti giới thiệu vào năm 1998. Một số đặc điểm của Alamouti STBC:
Mô hình sử dụng 2 anten phát và không giới hạn số anten thu - Nr. Điều đó có nghĩa là có thể sử dụng 1 anten thu.
Bậc phân tập anten là tích của số anten phát và anten thu tương ứng là 2Nr.
Alamouti STBC sẽ không cải thiện tốc độ truyền dữ liệu thay vào đó là chất lượng tín hiệu sẽ được cải thiện đáng kể.
Mô hình hệ thống:
Tín hiệu được truyền dựa trên 2 anten phát và được đóng gói thành một nhóm 2 symbols. Ở khe thời gian thứ nhất, symbols x1, x2 được truyền tương ứng từ anten thứ nhất và thứ hai. Ở khe thời gian thứ hai, symbols –x2* và x1* sẽ được truyền tương ứng từ anten thứ nhất và thứ hai. Tương tự như thế, symbols x3, x4 ở khe thời gian thứ ba, rồi –x4*, x3* cho khe thời gian thứ bốn. Vì vẫn cần 2 khe thời gian để truyền 2 symbols nên tốc độ sẽ không được cải thiện.
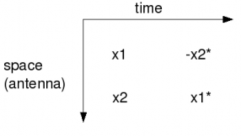
Hình 2.5. Symbol được truyền qua 2 anten phát.
Với Nr=1, ở đầu thu
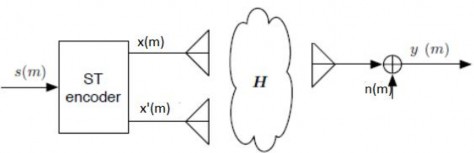
Hình 2.6. Hệ thống Alamouti STBC 2x1 Tại khe thời gian thứ nhất tín hiệu nhận được có dạng:
y h x h x n h h
x1 n
( 2.2)
1 1 1 2 2 1 1
2 x 1
2
Tại khe thời gian thứ hai tín hiệu nhận được có dạng:
x*
y h x* h x* n h h 2 n
( 2.3)
x
2 1 2 2 1 2 1
2 * 2
1
Với:
y1,y2 lần lượt là symbols nhận được ở khe thời gian thứ nhất và thứ hai h1,h2 lần lượt là hàm truyền từ anten thứ nhất và thứ hai đến anten thu x1,x2 là symbols truyền đi
n1,n2 là nhiễu tại khe thời gian thứ nhất và thứ hai
Có thể viết gọn lại bằng cách kết hợp (2.2)
y h x h x n h h
x1 n
( 2.2)và liên hợp phức
1 1 1 2 2 1 1
2 x 1
của (2.3):
2
ℎ1 ℎ2
y1 x1 n1 x1 n1
[ ] = [ ] [ ] + [ ] = H [ ] + [ ] ( 2.4)
y∗ ℎ∗ −ℎ∗ x2 n∗
x2 n∗
2 2 1 2 2
Với H = [ℎ1 ℎ2 ], cần tìm nghịch đảo của H để có thể giải hệ phương trình
ℎ∗ −ℎ∗
2 1
tìm được
x1 . Với định nghĩa hàm đảo Pseudo của ma trận:
[x2]
H+ = (HKH)–1HK ( 2.5)
Nhân H+vào phương trình (2.4):
xˆ1y1x1n1
[ ] = (HKH)–1HK [ ] = (HKH)–1HK (H [ ] + [ ])
y
n
x
∗
2
2 2
x1 K
x2 ∗
–1 K n1
n
= [x2] + (H H)
H [ ∗] 2
( 2.6)
Kết quả ở (2.6) cho thấy tín hiệu nhận được bao gồm tín hiệu phát và bộ phận
của nhiễu.
[xˆ1] x2
sau đó có thể được đưa qua bộ Maximum likelihood Decoder để chọn
ra tín hiệu phát phù hợp.
Tổng quát với Nr=i:
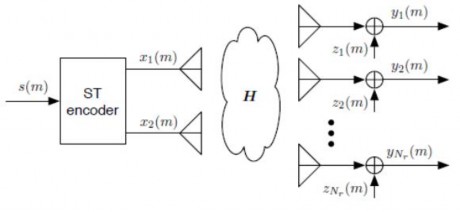
Hình 2.7. Alamouti STBC với nhiều anten thu
Tại đầu phát, thông tin được truyền tại thời điểm m và tiếp đó một khe thời
gian:
x1(m) x1(m + 1) s(m) −s∗(m + 1)
x
s
X = [
2
(m) x2
(m + 1)] = [ (m + 1)
s∗(m) ] ( 2.7)
Tại đầu thu, anten thu thứ i ,
[ yi(m)
ℎi1 ℎi2
] = [
] [ s(m) ] + [ zi(m) ]
y∗(m + 1) ℎ∗ −ℎ∗
s(m + 1)
z∗(m + 1)
i i2
= H [ s(m)
i1
zi(m)
i
] + [
i
] ( 2.8)
s(m + 1)
z∗(m + 1)
SNR tại anten thứ i,
SNRi
= (|ℎi1
|2 + |ℎi2
|2) Ps
Pz
( 2.9)
SNR cho Nr anten:
i=1
i1
SNR = ∑Nr (|ℎ
|2 + |ℎi2
|2) Ps
Pz
( 2.10)
Nhìn chung, mô hình alamouti STBC có chất lượng tốt hơn so với các hệ thống SISO. Điều đó thể hiện ở tỉ lệ lỗi bit BER. BER thường được tính theo hàm xác suất:
BER = 1 (1 − erf)ƒE /N
( 2.11)
2 b o
Trong đó erf là hàm xác suất lỗi, khác nhau đối với các kỹ thuật điều chế khác nhau nhưng nhìn chung chúng tỉ lệ với SNR. SNR càng lớn thì BER càng tốt. SNR
của một hệ thống SISO có thể tính bằng |ℎ| Ps. So sánh với (2.11), ta có thể nhận thấy
Pz
STBC cho BER tốt hơn SISO ngay cả khi dung cùng một công suất phát.
2.1.5 MIMO – STBC 2x2.
Xét hệ thống MIMO STBC 2 x 2:
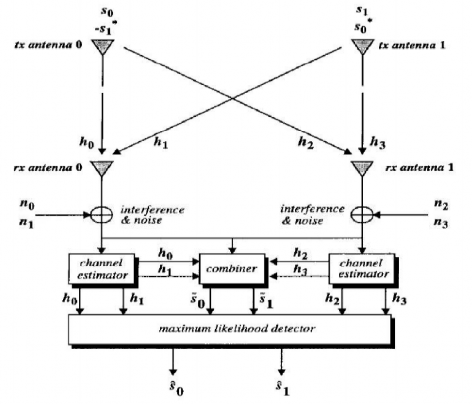
Hình 2.8. Mô hình STBC 2x2
Xét tín hiệu truyền đi sau. Cần lưu ý là tốc độ so với hệ thống SISO vẫn không thay đổi do vẫn tốn 2 khe thời gian để truyền 2 symbols:
y11
Hình 2.9. Mô hình STBC 2x2 Tại khe thời gian thứ nhất, tín hiệu thu được có dạng:
[ ] = [ℎ11 ℎ12] sO nO] ( 2.12)
y12
ℎ21
ℎ22
[s1] + [n1
Và tín hiệu nhận được ở khe thời gian thứ hai:
y21
ℎ11 ℎ12
−s∗ n2
[y22
] = [
] [
ℎ21 ℎ22
1] + [
s
∗
n
O 3
] ( 2.13)
y11
Trong đó: [y12] lần lượt là tín hiệu thu được tại anten thứ nhất và thứ 2 tại thời
điểm thứ nhất, [y21] là tín hiệu thu được tại anten thứ nhất và thứ 2 tại thời điểm thứ
y22
2. Và hij
là hàm truyền từ anten phát thứ j đến anten thứ i. [nO] là nhiểu xảy ra tại thời
n1
n2
điểm thứ nhất, và tương ứng với thời điểm thứ 2 là [n3].
Kết hợp cả hai thời điểm, hai khe thời gian ta được:
ℎ
y11 y12
ℎ11 ℎ12 nO
n
s1
ℎ21 ℎ22 sO n1
[y21
y22
∗] = [ ∗
12
ℎ
∗ ∗
22
∗ ] [
−ℎ
11
−ℎ
∗ 21
] + [ ∗] ( 2.14)
2
n
∗ 3
Tương tự như trên, để giải tìm được tín hiệu truyền ta cần phải dựa vào khái niệm ma trận đảo Psuedo của H, H+ = (HKH)–1HK . Với
ℎ11∗ ℎ21∗
ℎ12 ℎ22
ℎ11 ℎ12
ℎ
ℎ21 ℎ22
HKH = [
ℎ12∗
ℎ22∗
−ℎ11 −ℎ21
] [ ∗ 12
∗ ] ( 2.15)
−ℎ
11
ℎ∗ −ℎ∗
22 21
K |ℎ11|2 + |ℎ12|2 + |ℎ21|2 + |ℎ22|20
H H = [
0 |ℎ11
|2 + |ℎ12
|2 + |ℎ21
|2 + |ℎ22
|2]
( 2.16)
1
⎡ 2 2 2 2 0 ⎤
⎢
(HKH)–1 = ⎢|ℎ11|
+ |ℎ12|
+ |ℎ21|
+ |ℎ22| ⎥
0 1 ⎥
⎣ |ℎ11|2 + |ℎ12|2 + |ℎ21|2 + |ℎ22|2⎦
( 2.17)
Khi đó