Hệ Siêu Tĩnh Đối Xứng Và Phản Xứng X 1 , X 2 , X 3 Là Nghiệm Của Phương Trình

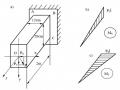
Hình 2.4: Hệ tĩnh định tương đương

Với mỗi phản lực liên kết Xi ta có một điều kiện chuyển vị: chuyển vị i của hệ theo phương của phản lực liên kết Xi : i 0 (2.1)

Nếu hệ siêu tĩnh có n bậc siêu tĩnh thì sẽ có n phương trình (2.1). Gọi là hệ phương trình chính tắc xác định các phản lực liên kết Xi (i = 1, 2, .., n):

1 11 1 12 2 1n n 1p

X X ... X 0 

X X ... X 0 

2 21 1 22 2 2 n n 2p 



............................................................. 

Có thể bạn quan tâm!

Xem toàn bộ 91 trang tài liệu này.

(2.2)

X X ... X 0

n n1 1 n2 2 nn n np 

trong đó: ip là chuyển vị theo phương i của hệ cơ bản do tải trọng gây nên. ik là chuyển vị đơn vị theo phương i của hệ cơ bản do lực đơn vị đặt theo phương k gây nên. i là chuyển vị theo phương của lực Xi do tải trọng và phản lực liên kết.

Ta có thể biểu diễn hệ phương trình (2.2) dưới dạng ma trận. Giải hệ (2.2) bằng phương pháp Gauss, Cramer, … hoặc giải qua các chương trình máy tính như MATLAB, MAPLE, …

Ta có thể tính được ip và ik theo công thức Mo sau:



li M M

i k dz

; 

li M M

i p dz

(2.3)

ik 

i1 0

ip 

i1 0

Sau khi xác định được các phản lực liên kết Xi, đặt các phản lực liên kết Xi cùng với tải trọng lên hệ cơ bản ta được một hệ tĩnh định tương đương.

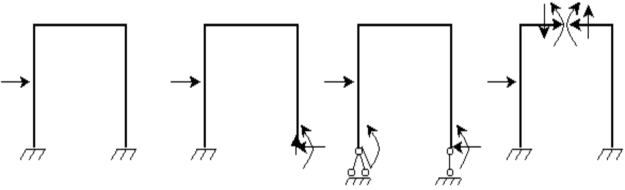
Giải hệ siêu tĩnh bằng phương pháp lực ta có các bước sau:

Bước 1. Xác định bậc siêu tĩnh và chọn hệ cơ bản

Bước 2. Xác định hệ tĩnh định tương đương bằng cách đặt vào hệ cơ bản các phản lực liên kết tương ứng với các liên kết thừa đã bỏ đi.

Bước 3. Thiết lập hệ phương trình chính tắc

2.2.3. Tính hệ siêu tĩnh đối xứng

a. Định nghĩa

Hệ đối xứng là hệ có ít nhất một trục đối xứng.

Hệ đối xứng chịu tải trọng đối xứng khi tải trọng đặt lên phần này là ảnh của tải trọng đặt lên phần kia qua gương phẳng đặt tại trục đối xứng và vuông góc với mặt phẳng của hệ.

Nếu tải trọng của phần này là ảnh của phần kia nhưng có chiều ngược lại thì ta gọi là hệ đối xứng chịu tải trọng phản đối xứng.

Hình (2.5a,b,c) : Hệ siêu tĩnh đối xứng, hệ chịu tải trọng đối xứng, hệ chịu tải trọng phản đối xứng.

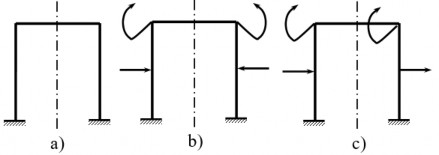
Hình 2.5 : Hệ siêu tĩnh đối xứng

b. Tính chất

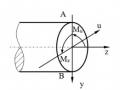
Tương tự, nội lực cũng có tính chất đối xứng hoặc phản đối xứng. Trong mặt phẳng: Nz , Mx có tính đối xứng, Qy có tính phản đối xứng Trong không gian: Nz, Mx, My là đối xứng, Qx, Qy và Mz phản đối xứng.

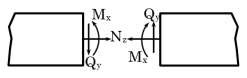
Hình 2.6: Nội lực trong mặt phẳng

Tính chất của hệ siêu tĩnh đối xứng:

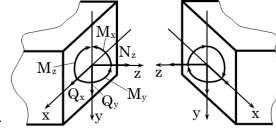
Hình 2.7: Nội lực trong không gian

Nếu một hệ siêu tĩnh đối xứng chịu tải trọng đối xứng thì nội lực phản đối xứng trên mặt cắt trong mặt phẳng đối xứng của hệ là bằng không. Ngược lại nếu tải trọng là phản đối xứng thì nội lực đối xứng phải bằng không.

Chú ý các nhận xét sau: Khi hệ là đối xứng chịu tải trọng đối xứng thì biểu đồ mômen là đối xứng, ngược lại nếu tải trọng phản đối xứng thì biểu đồ mômen là phản đối xứng.

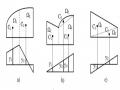
Chứng minh: Giả sử có hệ siêu tĩnh đối xứng chịu tải phản đối xứng (hình 2.8b). Chọn hệ cơ bản bằng cách cắt đôi khung. Phải chứng minh các thành phần nội lực đối xứng X1 và X2 trên mặt cắt là bằng không.

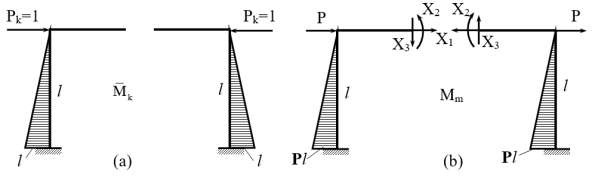
Hình 2.8 : Hệ siêu tĩnh đối xứng và phản xứng X1 , X2 , X3 là nghiệm của phương trình chính tắc:

X X X 0

11 1 12 2 13 3 1p

21X1 22X2 23X3 2p 0

(2.4)

X X X 0

31 1 32 2 33 3 3p

Biểu đồ

M1 ,

M2 là đối xứng còn biểu đồ

M3 là phản đối xứng nên:

13 = 31 = 23 = 32 =1p = 2p = 0

Do đó hệ phương trình chính tắc trên thu gọn lại như sau:

X X 0

11 1 12 2

21X1 22X2 0

(2.5)

X 0

33 3 3p

Hai phương trình đầu là một hệ thống phương trình thuần nhất 2 ẩn số định thức khác không, do đó X1 = X2 = 0.

Tương tự, khung chịu lực đối xứng như hình vẽ 2.8a. Lúc đó biểu đồ tải trọng là đối

xứng nên:

13 = 31 = 23 = 32 = 3P = 0

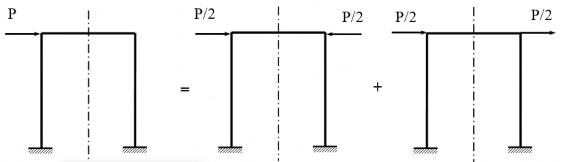
Hình 2.9: Giải bài toán khung bằng cách sử dụng hệ siêu tĩnh đối xứng và phản xứng

Hệ phương trình chính tắc:

11X1 12 X2 1p 0

X X 0



21 1 22 2 2p

(2.6)



33X3 0

Từ phương trình thứ 3 ta được X3 = 0 .

Trường hợp hệ đối xứng nhưng tải trọng bất kỳ thì bằng tổng tác dụng của hệ có tải trọng đối xứng và hệ chịu tải trọng phản đối xứng (hình 2.9)

2.3. DẦM LIÊN TỤC

2.3.1. Định nghĩa

Dầm liên tục là dầm siêu tĩnh đặt trên nhiều gối tựa đơn, trong đó có một gối tựa cố định (hình 2.10a). Khoảng cách giữa hai gối tựa gọi là nhịp. Bậc siêu tĩnh của dầm bằng số nhịp trừ đi một.

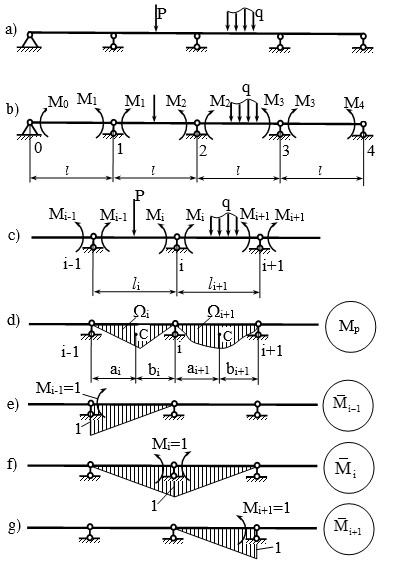
Hình 2.10: Dầm liên tục

2.3.2. Phương trình ba mômen

Chọn hệ cơ bản của dầm bằng cách đặt lên mỗi gối tựa một khớp để chia dầm thành nhiều dầm đơn (h×nh 2.10b).

Những lực tác dụng lên một nhịp nào đó chỉ ảnh hưởng đến chuyển vị của nhịp bên cạnh nên khi xét chuyển vị ở một gối tựa bất kỳ, chỉ cần xét hai nhịp liên tiếp nhau

và các ẩn số chỉ là các mômen uốn nội lực Mi (h×nh 2.10c) (Mi>0 làm căng thớ dưới).

Phương trình chính tắc: viết theo điều kiện góc xoay tương đối giữa hai mặt cắt tại gối tựa đó phải bằng không.

Ví dụ tại gối tựa thứ “i”:

11M1 + 12M2 +…+ i,i-1Mi-1 + i,iMi + i,i+1Mi+1 +…+ 1nMn + ip = 0

Các hệ số i1 = i2 = …= i(i-2) = … = 0, do lực tác dụng trên hai nhịp ở trên hai gối tựa thứ “i” chỉ ảnh hưởng đến góc xoay của gối tựa trên hai nhịp đó. Phương trình chính tắc của hệ có dạng sau:

i,i-1Mi-1 + i,iMi + i,i+1Mi+1 + ip = 0 (2.7) Các hệ số và số hạng tự do trong (2.7):

li1 M M 1 1 1 l

i,i1 

i1 idz 

. .1.li.

i

0 EJi

EJi

2 3 6EJi

li M M 1 1 2 1 1 2 l l

i,i i idz 

. .1.li. 

. .1.li1.

ii1

0 EJ EJi

2 3 EJi1

2 3 3EJi

3EJi1

li1 M M 1 1 1 l

i,i1 

i i1dz 

. .1.li1.

i1

0 EJi1

EJi1

2 3 6EJi1

li MpMi

ip 

dz 

1 . .ai

1 bi1

. .

i1

0 EJ EJi

li EJi1

li1

trong đó: li, li+1 : độ dài của nhịp thứ i và thứ (i+1). i, i+1: Diện tích của biểu đồ mômen do tải trọng gây nên trên hai nhịp thứ i và thứ (i+1). ai, bi+1: Khoảng cách từ trọng tâm của các diện tích đó đến gối tựa thứ (i-1) và (i+1).

Thay các trị số đó vào phương trình chính tắc, ta có:

li M

li

li1

 M 

li1 M

i .ai i1.bi1  0

(2.8)

6EJi

i1

 3EJi

3EJi1 i

6EJi1

i1

liEJi

li1EJi1 



NÒu ®é cøng EJ kh«ng ®æi trªn suèt chiÒu dµi cđa dÇm, ta cã :

l M  2l l M l M

 6i.ai i1.bi1  0

(2.9)

i i1 i i1 i i1 i1

li li1 



Ví dụ 2.1 :

Vẽ biểu đồ lực cắt, mômen uốn của dầm liên tục như hình vẽ 2.11a

Giải:

Đây là hệ siêu tĩnh bậc 2. Hệ cơ bản như hình 2.11b. Biểu đồ mômen uốn Mp như hình 2.11c.

Phương trình ba mômen đối với gối tựa thứ 1, 2 và 3 là:

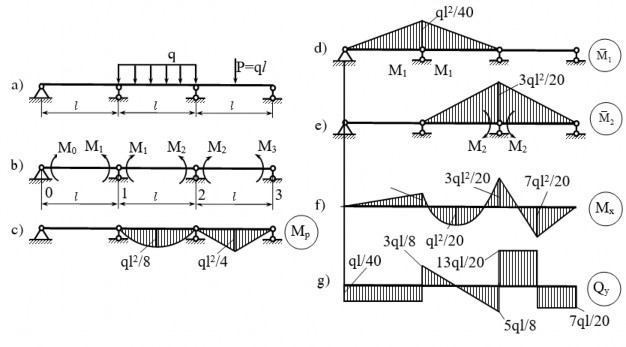
Hình 2.11 : Hình ví dụ 2.1



lM0 2(l + l)M1 lM2 6 0 

2 ql2

. .l.

1 

0

3 8 2 

2 ql2 11 ql2 1

lM 2(l + l)M lM 6 . .l. . .l. 0

1 2 3



3 8 2 2 4 2 

Trong đó M0 = M3 = 0 (do các khớp không có mômen ngoại lực tập trung). Giải ra

ta được: M ql

1 40

; M 3ql

2 20

Dấu (-) chỉ các m«men có chiều ngược với chiều đã chọn.

Cộng các biểu đồ Mp, M1, M2 ta được biểu đồ Mx (hình 2.11f). Sau khi tính phản lực các gối tựa của biểu đồ Mp, M1, M2 và cộng các vectơ phản lực, ta thu được biểu đồ Qy như trên hình 2.11g.

2.3.3. Trường hợp đặc biệt

Trường hợp dầm liên tục có đầu thừa và đầu ngàm thì cách giải của chúng ta như sau:

Tưởng tượng bỏ đầu thừa và thu gọn tất cả ngoại lực đặt trên đoạn đó về gối tựa cuối cùng. Mômen uốn thu gọn có thể xem là mômen liên kết tại mặt cắt của gối tựa cuối cùng (mômen đó có trị số dương khi nó làm căng thớ dưới và có trị số âm khi nó làm căng thớ trên) hoặc được xem là mômen uốn ngoại lực tác động lên dầm. Còn liên kết ngàm thì được thay bằng một nhịp đặt trên một gối tựa cố định và một liên kết đơn. Ðộ cứng EJx của đoạn nhịp này được xem là lớn vô cùng và chiều dài của nhịp đó được xem là bằng không (hình 2.12).

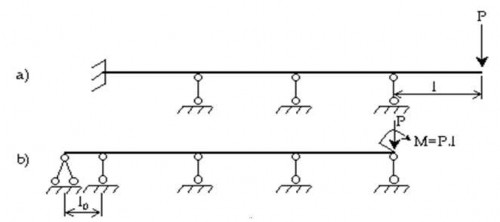
Hình 2.12 : Dầm liên tục có đàu thừa và đầu ngàm

Phương trình ba mômen được áp dụng đối với từng nhịp cạnh như phần trên.

Ví dụ 2.2:

Vẽ biểu đồ nội lực của dầm chịu lực như hình vẽ (2.13a).

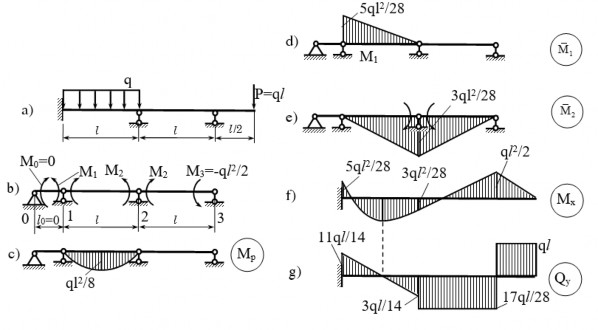
Hình 2.13 : Hình ví dụ 2.2

Giải:

Hệ cơ bản và thứ tự các nhịp, các gối tựa được đánh số như hình 2.13b. Biểu đồ Mp do tải trọng gây nên trên hệ cơ bản như hình 2.13c.

Mômen thu gọn ở gối tựa cuối cùng được xem là mômen liên kết trên mặt cắt của

gối tựa đó. Vì vậy trên biểu đồ mômen Mp không có mômen đó. Với các gối tựa (1), (2), ta thiết lập được các phương trình ba mômen như sau:

2 ql21

lM0 2(l + l)M1 lM2 6 . .l. 0

3 8 2



2 ql21

lM1 2(l + l)M2 lM3 6 . .l. 0

3 8 2

Giải hệ trên với M0 = 0 và M3 = 0.5Pl = 0.5ql2 ta được:



;

5ql2

M2 

3ql2 28

Mômen M1<0, chứng tỏ mômen M1 làm căng thớ trên, mômen M2>0 có nghĩa là M2 làm căng thớ dưới. Biểu đồ mômen uốn và lực cắt cho trên hình 2.13f,g.

2.4. PHÉP NHÂN BIỂU ĐỒ VÊRÊXAGHIN

Xác định chuyển vị của các thanh có độ cứng không đổi, theo công thức Mo khá phức tạp. Đối với hệ thanh thẳng, ta thấy ít nhất một hàm nội lực dưới dấu tích phân là bậc nhất hoặc hằng số.

Nếu một trong hai hàm số dưới dấu tích phân có dạng bậc nhất thì ta có thể thay cách giải tích phân trên bằng phương pháp nhân biểu đồ của Vêrêxaghin.

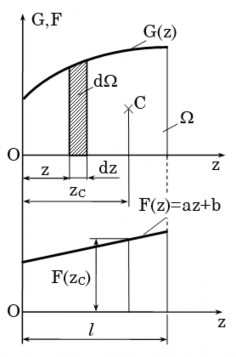
Hình 2.14: Phép nhân biểu đồ Vêrêxaghin

Nội dung phương pháp như sau:

Giả thiết trên đoạn chiều dài l nào đó của thanh, hàm số G(z) có dạng bất kỳ còn F(z) có dạng bậc nhất: F(z) = (az + b)

 Tích phân



Mk Mmdz F(z).G(z)dz , trong đó

F(z) Mk

còn

G(z) Mm .

 Tích phân I của hai hàm số F(z) và G(z):

l l

I F(z).G(z)dz (az b).G(z)dz

0 0

với d = G(z)dz là một diện tích vô cùng nhỏ của biểu đồ G(z), ta có tích phân theo biến mới: I (az b)dazdbdazdb

