Khái Niệm, Phương Trình Vi Phân Của Đường Đàn Hồi

đã nêu trong các chương trước.

Thực tế cho thấy thanh có thể mất ổn định trong giới hạn đàn hồi, khi ứng suất chưa vượt quá giới hạn tỷ lệ tl, và thanh cũng có thể mất ổn định ngoài giới hạn đàn hồi, khi ứng suất trong thanh vượt quá giới hạn tỷ lệ tl.

Hiện tượng mất ổn định cũng có thể xảy ra đối với các trường hợp chịu lực khác của thanh. Ví dụ như:

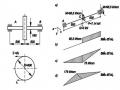
- Hình 3.4a: Dầm chịu uốn sẽ ổn định khi lực ngang P Pth, trong dầm chỉ có biến dạng uốn, khi P Pth thì dầm mất ổn định, ngoài biến dạng uốn dầm còn có biến dạng xoắn.

- Hình 3.4b: Một ống tròn mỏng bị xoắn thuần tuý khi mômen xoắn M > Mth, thành ống sẽ bị méo vì mất ổn định.

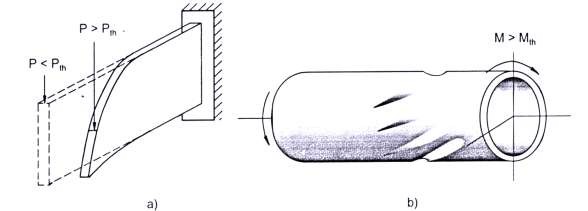
Hình 3.4: Một số dạng mất ổn định khác

Ngày nay, vấn đề ổn định kết cấu đã được quan tâm nghiên cứu và được trình bày trong những chuyên đề, giáo trình riêng biệt. Trong khuôn khổ sức bền vật liệu ta chỉ nghiên cứu bài toán cơ bản nhất: bài toán ổn định của thanh thẳng chịu nén đúng tâm, hoặc còn gọi là bài toán uốn dọc (thanh cong khi chị tác dụng của lực dọc trục), mà mục đích chính là xác định lực nén tới hạn để kiểm tra điều kiện ổn định.

3.2. BÀI TOÁN EULER XÁC ĐỊNH LỰC TỚI HẠN

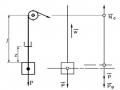
3.2.1. Thanh thẳng liên kết khớp ở hai đầu

Xét một thanh thẳng liên kết khớp ở hai đầu, chịu lực nén đúng tâm N có phương không đổi. Giả sử lực nén đạt tới trị số tới hạn N = Nth, thanh bị uốn cong và tiết diện ở tọa độ z có độ vòng y 0 nằm trong mặt phẳng có độ cứng chống uốn nhỏ nhất như trên hình 3.5.

Ký hiệu độ cứng chống uốn trong mặt phẳng đang xét của tiết diện là EI, mô men uốn tại tiết diện là M, ta có phương trình vi phân độ vòng là:

y'' M

(3.1)

Bằng phương pháp mặt cắt, xét thanh ở trạng thái biến dạng như trên hình 3.5b,

ta có :

M = N.y (a)

z M

Hình 3.5: Bài toán Euler

Thay (a) vào 3.1 ta nhận được phương trình vi phân cấp hai thuần nhất:

y'' 2 y  0

(3.2)

với ký hiệu:

2 N

(3.3)

Nghiệm tổng quát của phương trình là:

y C1cosz C2 sinz

(b)

Các hằng số tích phân được xác định từ các điều kiện biên:

Tại z = 0 thì y = 0; thay vào (b) ta có: C1 = 0 ; do đó y = C2sinz (c) Tại z = l thì y = 0 ; thay vào (c) ta có : C2sinl=0 (d) Như vậy, hoặc C2 = 0 hoặc sinl = 0

Theo (c) điều kiện C2 = 0 dẫn đến kết luận y = 0, trái với giả thiết ban đầu là y

0 như vậy sinl = 0. Do đó :

k2

l k

với k là số tự nhiên, hoặc 

l

(e)

So sánh(3.3) và (e) ta suy ra :

N k 2 2 EI



với k = 1,2,3,… (3.4)

Biểu thức (3.4) là điều kiện để độ vòng của thanh khác không, tức là điều kiện mất ổn định của thanh. Giá trị bé nhất khác không của (3.4) ứng với k = 1 sẽ là lực tới hạn.

Nth

2 EI

(f)

Mặt khác, trên tiết diện của thanh tồn tại hai trục quán tính chính trung tâm, là hai trục trung tâm có mô men quán tính cực trị là Imax và Imin. Để có giá trị bé của (f)

thì ta sử dụng Imin, có nghĩa là thanh sẽ cong trong mặt phẳng có độ cứng chống uốn EI

bé nhất. Biểu thức lực tới hạn khi này là:

2 EI

Nth 

min

(3.5)

Như thế, lực tới hạn là lực nén nhỏ nhất tạo cho thanh thêm một dạng cân bằng cong khác với dạng cân bằng thẳng ban đầu.

Theo các kết luận trên, ta có thể nhận thấy một vài vấn đề chưa được giải quyết

rành mạch, chẳng hạn độ vòng của thanh có dạng

y C2

sin z

nhưng trị số của độ

vòng không xác định, hoặc dạng độ vòng sẽ ra sao nếu tải trọng nhận giá trị lớn hơn trị

2 EI

số ứng với k=1 là

2 EI

Nth 

min nhưng nhỏ hơn trị số tới hạn ứng với k = 2 là

…

Nth,2  4 min

Để trả lời các câu hỏi này ta cần lưu ý rằng công thức Euler được xây dựng trên cơ sở phương trình vi phân tuyến tính gần đúng của độ vòng, phương trình này chỉ được chấp nhận khi biến dạng nhỏ, công thức Euler chỉ cho giá trị lực tới hạn ở thời điểm thanh bắt đầu cong mà không kết luận về quá trình tiếp tục cong của thanh. Lagrange đã lặp lại nghiên cứu của Euler nhưng xuất phát từ phương trình vi phân phi

tuyến chính xác của đường đàn hồi

y''

1y'232

M

và đã kết luận rằng: khi lực nén

đạt giá trị của Euler thì thanh bắt đầu cong và sau đó dù lực tăng rất ít, biến dạng của thanh sẽ phát triển rất nhanh dẫn thanh tới trạng thái bị phá hủy. Vì vậy, khi không có các liên kết phụ để hạn chế độ vòng thì chỉ xảy ra đường cong ứng với k=1, không tồn tại những đường biến dạng ứng với các trị số cao hơn.

3.2.2. Thanh thẳng có liên kết khác ở hai đầu

Lặp lại phép giải bài toán đã tiến hành ở trên nhưng thay đổi các điều kiện biên, ta nhận được biểu thức của lực tới hạn trong từng trường hợp liên kết cụ thể của thanh và có thể viết một cách tổng quát:

Nth

2EImin

l 2

(3.6)

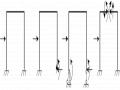
Trong đó là hệ số phụ thuộc điều kiện liên kết ở hai đầu thanh, trị số cho trên hình 3.1.

Nghiên cứu tỷ mỷ hơn có thể thấy là số lần chiều dài của thanh ứng với một nửa bước song hình sin của đường cong trục thanh. Chẳng hạn hai lần chiều dài đối với thanh côngxôn, một lần chiều dài đối với thanh liên kết khớp ở hai đầu, một nửa

chiều dài đối với thanh liên kết ngàm ở hai đầu.

a) b) c) d)

lo /2

lo lo

2

1 0,7

0,5

Hình 3.6: Hệ số ảnh hưởng liên kết (l0=l)

Trị số l0=l được gọi là chiều dài quy đổi của thanh khi tính ổn định. Công thức tính lực tới hạn theo chiều dài quy đổi là:



2EImin

th 2

(3.7)

Bài toán tìm lực tới hạn của thanh thẳng chịu nén đúng tâm được Euler giải lần đầu tiên vào năm 1744 và công thức tính lực tới hạn (3.6) được gọi là công thức Euler.

Công thức Euler sử dụng trị số Imin đúng với trường hợp thanh có liên kết như nhau trong hai mặt phẳng quán tính chính xz và yz. Khi thanh có liên kết khác nhau trong hai mặt phẳng thì cần tính lực tới hạn riêng biệt trong từng mặt phẳng và chọn trị số nhỏ hơn làm lực tới hạn thực.

3.3. ỨNG SUẤT TỚI HẠN. GIỚI HẠN ÁP DỤNG CÔNG THỨC EULER

3.3.1. Ứng suất tới hạn, độ mảnh

Thương số giữa lực tới hạn Nth và diện tích A của tiết diện là ứng suất trên tiết diện thanh ngay trước thời điểm thanh bị mất ổn định, được gọi là ứng suất tới hạn, ký hiệu th. Có thể viết:

Nth 2 EImin 

2 E

(3.8)

th Al 2A

l

r 

Imin

min 

Với:

rmin

là bán kính quán tính nhỏ nhất của tiết diện.

Gọi  là độ mảnh của thanh:

l

rmin

(3.9)

Ta nhận được công thức tính ứng suất tới hạn của Euler:

2 E

(3.10)

th 2

Độ mảnh  là một đặc trưng ổn định của thanh, trị số này càng lớn thì khả năng ổn định của thanh càng nhỏ, tên gọi “độ mảnh” cũng xuất phát từ ý nghĩa: càng mảnh thì càng dễ mất ổn định. Độ mảnh phụ thuộc vào chiều dài của thanh, điều kiện liên kết và đặc trưng hình học của tiết diện.

3.3.2. Giới hạn áp dụng công thức Euler

Phương trình vi phân đường đàn hồi (3.1), cơ sở để giải bài toán Euler, chỉ đúng khi vật liệu làm việc trong giới hạn đàn hồi. Do đó, kết quả của bài toán cũng chỉ đúng khi vật liệu còn làm việc trong giới hạn đàn hồi, tức là khi ứng suất trong thanh nhỏ hơn giới hạn tỷ lệ:

th

2 E 

2 E

tl

2 tl



hoặc khi: (g)

Nếu ký hiệu:

0 

(3.11)

2 E

tl

Thì điều kiện để áp dụng công thức Euler là:

0

(3.12)

Thanh có độ mảnh thỏa mãn điều kiện (3.12) được gọi là thanh có độ mảnh lớn. Thanh có độ mảnh nhỏ hơn 0 được gọi là thanh có độ mảnh vừa hoặc bé.

Không thể áp dụng công thức Euler để tính ứng suất tới hạn đối với thanh có độ mảnh

vừa và bé.

3.4. ỔN ĐỊNH CỦA THANH LÀM VIỆC NGOÀI GIỚI HẠN ĐÀN HỒI

Nghiên cứu lý thuyết về ổn định ngoài giới hạn đàn hồi còn gặp những khó khăn nhất định và chưa cho một kết quả thống nhất. Trong kỹ thuật ta thường áp dụng những công thức đơn giản rút ra từ thực nghiệm.

1. Thanh có độ mảnh vừa: 1 ≤ ≤ 0

Có thể dùng công thức của Iasinski:

th=a - b(3.13)

Hằng số a, b phụ thuộc vào vật liệu và tìm được từ thí nghiệm: Với thép ít cacbon: a=31 kN/cm2; b=0,14 kN/cm2 Với gỗ: a=2,93 kN/cm2; b=0,0194 kN/cm2

Quan hệ giữa th và là bậc nhất. Có thể tìm được giới hạn 1 theo biểu thức:

2. Thanh có độ mảnh bé ≤1

a tl

1 b

Vì độ mảnh quá bé nên khi chịu nén thì thanh không thể bị cong, trạng thái tới hạn của thanh cũng đồng thời là trạng thái phá hủy của vật liệu. Sự phá hủy này mang đặc trưng giòn, chẳng hạn với bê tông, khi ứng suất đạt giới hạn bền; hoặc mang đặc trưng xuất hiện biến dạng dẻo, chẳng hạn với thép, khi ứng suất đạt giới hạn chảy.

th

b





(3.14)

ch

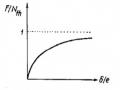
Đồ thị quan hệ giữa ứng suất tới hạn th và độ mảnh  của thanh làm từ vật liệu dẻo được vẽ trên hình 3.3.

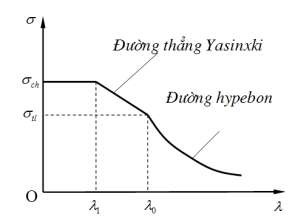
Hình 3.7: Quan hệ th và 

3.5. PHƯƠNG PHÁP THỰC HÀNH TÍNH ỔN ĐỊNH Ta đã biết điều kiện bền của thanh chịu nén là:



(3.15)

Trong đó:

N – giá trị lực dọc;

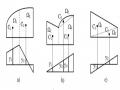
A – diện tích tiết diện giảm yếu cục bộ của thanh, chẳng hạn với hệ số trên hình 3.8, trị số A là A0 lấy tại tiết diện có khoét lỗ;

[] - ứng suất bền cho phép, bằng ứng suất tới hạn 0 chia cho hệ số an toàn về

bền:

dạng:

0

Điều kiện ổn định của thanh chịu nén, kể đến hệ số an toàn, có thể viết dưới

Aod

th

(3.16)

Sự giảm yếu của một vài tiết diện không ảnh hưởng đáng kể đến độ ổn định

chung của thanh, do đó diện tích A sẽ lấy bằng diện tích nguyên của thanh.

Trị số ứng suất tới hạn lấy theo các công thức (3.10), (3.13), (3.14) tùy theo độ mảnh của thanh. Để giảm bớt khó khăn khi tính toán, ta đưa thêm ký hiệu:

od



(h)

Khi đó, điều kiện ổn định (3.16) được viết lại, có dạng tương tự điều kiện bền

như sau:

A 

(3.17)

A A0

Hình 3.8: Diện tích tiết diện A và A0

Hệ số được gọi là hệ số uốn dọc hoặc hệ số giảm ứng suất cho phép, theo biểu thức định nghĩa sẽ là một hàm phụ thuộc độ mảnh

od

n.th 



k 0

Dạng hàm =() là đã biết và có thể lập sẵn thành bảng cho từng loại vật liệu.

Khi tính toán ta chỉ cần tra bảng tìm hệ số theo độ mảnh của thanh. Cách tính ổn định như vậy theo (3.17) được gọi là cách tính thực hành, cách tính theo theo quy phạm hoặc cách tính theo hệ số giảm ứng suất cho phép. Ưu điểm của cách tính này không chỉ ở chỗ đơn giản, gọn gàng mà còn chuẩn xác hơn, tập hợp được nhiều số

liệu thống kê hơn khi lấy tỷ số của hai hệ số an toàn n

Theo điều kiện ổn định ta cũng có ba bài toán cơ bản:

- Bài toán kiểm tra:

A 

( 3.18)

Nếu bất đẳng thức thỏa mãn thì thanh ổn định, không thỏa mãn thì thanh mất ổn

định.

Bài toán xác định lực nén cho phép:

N A

(3.19)

Bài toán thiết kế, xác định tiết diện:

A (3.20)

Riêng với bài toán thiết kế, cách giải có phần phức tạp hơn vì hệ số phụ thuộc vào độ mảnh , độ mảnh lại chưa biết vì tiết diện chưa xác định. Do đó, bài toán sẽ được giải bằng cách thử đúng dần, thay bài toán thiết kế bằng bài toán kiểm tra.

Bảng 3.1: Bảng tra hệ số 

Độ mảnh 

Trị số đối với
Thép số 2,3,4	Thép số 5	Thép C 	Gang	Gỗ
0	1,00	1,00	1,00	1,00	1,00
10	0,99	0,98	0,97	0,97	0,99
20	0,96	0,95	0,95	0,91	0,97
30	0,94	0,92	0,91	0,81	0,93
40	0,92	0,89	0,87	0,69	0,87
50	0,89	0,86	0,83	0,57	0,80
60	0,86	0,82	0,79	0,44	0,71
70	0,81	0,76	0,72	0,34	0,60
80	0,75	0,70	0,65	0,26	0,48
90	0,69	0,62	0,55	0,20	0,38
100	0,60	0,51	0,43	0,16	0,31
110	0,52	0,43	0,35	-	0,25
120	0,45	0,36	0,30	-	0,22
130	0,40	0,33	0,26	-	0,18
140	0,36	0,29	0,23	-	0,16
150	0,32	0,26	0,21	-	0,14
160	0,29	0,24	0,19	-	0,12
170	0,26	0,21	0,17	-	0,11
180	0,23	0,19	0,15	-	0,10
190	0,21	0,17	0,14	-	0,09
200	0,19	0,16	0,13	-	0,08