Diện Tích Và Hoành Độ Trọng Tâm Của Một Số Hình Phẳng

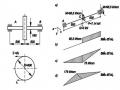
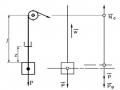
 Ta có

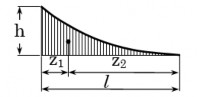
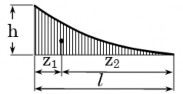
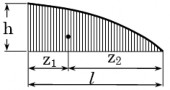
zdzC , trong đó zC là hoành độ trọng tâm của diện tích . Khi đó



tích phân I sẽ là:

I az b(az b)

C C

 Theo hình 10-12, ta có azC + b = F(zC) – tung độ của hàm F(z) ứng với hoành độ zC  I = F(zC) (2.10)

 Từ kết quả trên ta suy ra: nếu các biểu đồ nội lực Mm, Nm, Qm do tải trọng gây ra

có dạng bất kỳ, còn các biểu đồ

Nk , Mk , Qk

do tải trọng đơn vị có dạng bậc nhất thì:

1 M

M k C 

1 N

N k C 

1 Q Q

C 

(2.11)

km EJ m

EF m

GF m k

trong đó (Mm), (Nm), (Qm) là diện tích các biểu đồ Mm, Nm, Qm.

Mk (C), Nk (C),Qk (C) là các giá trị của biểu đồ

Mk , Nk ,Qk

tại những

vị trí tương ứng với trọng tâm của diện tích các biểu đồ Mm, Nm, Qm.

Cần chú ý rằng:

- Nếu cả hai biểu đồ nội lực do tải trọng và tải trọng đơn vị đều có dạng bậc nhất thì khi nhân ta có thể lấy diện tích của biểu đồ này nhân với tung độ tương ứng với biểu đồ kia hoặc ngược lại.

- Nếu chỉ có một biểu đồ là bậc nhất thì giá trị tung độ tương ứng tại trọng tâm bắt buộc phải lấy ở biểu đồ có dạng bậc nhất đó.

- Nếu đồ thị bậc nhất bị gãy khúc thì phải chia chiều dài lấy tích phân thành từng đoạn, trên mỗi đoạn đồ thị này là một đường thẳng trơn, để thực hiện phép nhân, sau đó lấy tổng kết quả phép nhân trong các đoạn.

- Kết quả của phép nhân mang dấu (+) khi diện tích và tung độ đều cùng dấu hoặc cùng nằm về một phía của đường chuẩn.

- Nếu các biểu đồ có dạng phức tạp thì khi nhân ta chia chúng ra nhiều hình đơn giản, sau đó ta cộng các kết quả lại với nhau.

- Kết quả của phép nhân biểu đồ đối xứng với biểu đồ phản đối xứng sẽ bằng không.

Hình 2.15

Bảng 2.1 - Diện tích và hoành độ trọng tâm của một số hình phẳng

Bậc 2 2 hl ; z 1 l z 3l 3 1 4 24
	Bậc n 2 hl ; z 1 l z 3 l 3 1 4 24
	Bậc 2 2 hl ; z 1 l z 3 l 3 1 4 24

Có thể bạn quan tâm!

• Thanh Mặt Cắt Ngang Tròn Chịu Uốn Đồng Thời Xoắn
• Trục Chịu Uốn Và Xoắn Đồng Thời Các Biểu Đồ Nội Lực Được Biểu Diễn Trên Các Hình 1.22B, C, D. Thay Số Vào Ta Được:
• Hệ Siêu Tĩnh Đối Xứng Và Phản Xứng X 1 , X 2 , X 3 Là Nghiệm Của Phương Trình Chính Tắc:
• Khái Niệm, Phương Trình Vi Phân Của Đường Đàn Hồi
• Quan Hệ Độ Vòng - Lực Nén (Dạng Không Thứ Nguyên)
• Bài Toán Kéo Vật Nặng Lên Cao Với Gia Tốc Không Đổi

Xem toàn bộ 91 trang tài liệu này.

Ví dụ 2.3:

Xác định chuyển vị thẳng đứng tại khớp A của một hệ chịu lực như hình vẽ (2.16a).

Diện tích MCN là F, môđun đàn hồi E.

Giải: Lực dọc trong các thanh:

Nz  P cot g30 

0 3P

1

Nz2

 P

sin 300

 2P

Tương tự trị số lực dọc ứng với Pk = 1:

k

;

N

k

N  3  2

1 2

Biểu đồ lực dọc Nm, Nk như hình 2.16c, 2.16d. Vì trong thanh chỉ có lực dọc nên:

y 1 .N (C ) .N (C )

A EF 

1 k 1 2 k 2 

3

Hình 2.16

Với: 1 = l

3P ;

Nk (C1) ;

2  2P.

1 

co s 300

4 Pl ;

Nk (C2 )  2 .

3

1 4

Pl 

3

8 3

yA l

EF

3P. 

Pl.2 3 

3

EF

3 



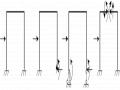
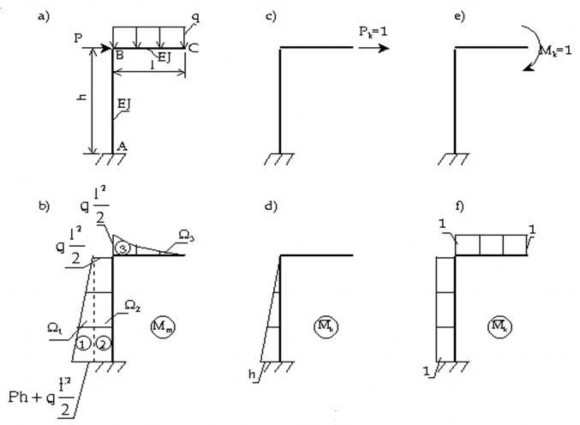
Ví dụ 2.4:



Cho khung chịu lực như hình vẽ 2.17a. Xác định chuyển vị ngang và góc xoay tại đầu tự do C.

Giải:

Biểu đồ Mm do tải trọng gây ra như hình vẽ (2.17b).

Ðể xác định chuyển vị ngang ta đặt lực theo phương ngang Pk=1 tại C, vẽ biểu đồ

2

Ph2

ql2 h h

Mk . Ta có: 1

Mk (C1 ) 

2

h ; 1 

3

Mk (C1 ) 

2 2

Nhân biểu đồ: 

11 Ph2. 2 h 1 ql2h 1 h 

1 1 Ph3 1 ql2h2 

C EJ  2 3 2 2  EJ  3 4 



Để xác định góc xoay tại C ta đặt tại C mômen Mk=1. Vẽ biểu đồ Mk .

1 Ph2 Mk (C ) 1;1 ql2 h Mk (C ) 1 ;

1 2 1 1 2 2

k

1ql3 M (C ) 1

1 63

Do đó: 

11 Ph2.11 ql2h.11 ql3.1

1 1 Ph2 1 ql2h 1 ql3 

C EJ  2 2 6  EJ  3 2 6 



Ví dụ 2.5: Cho khung chịu lực như hình vẽ (2.18a). Tính độ dịch gần tương đối giữa các trọng tâm MCN A và B. Bỏ qua ảnh hưởng của lực dọc và lực cắt; EJx=const

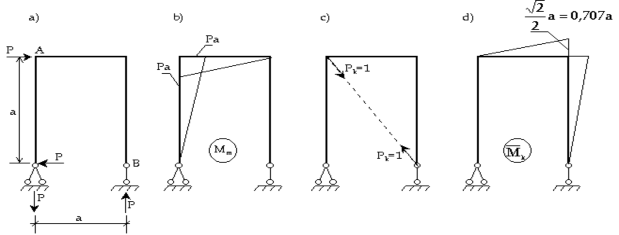
Hình 2.18

Giải:

Biểu đồ Mm như hình vẽ 2.18b

Ðể tìm chuyển vị thẳng tương đối km giữa A và B, đặt hệ lực suy rộng Pk = 1

ngược chiều nhau. Vẽ biểu đồ Mk

. Ta có:

n M 1 1 1 Pa3

km Mm k dz  Pa.a. 0, 707a. 0,118

i1

EJx

2 3 EJx

EJx

Dấu (-) ở đây chứng tỏ sau biến dạng các điểm A và B xa nhau hơn so với vị trí ban đầu của chúng (ngược chiều với các lực Pk=1).

2.5. CÁCH TÍNH CHUYỂN VỊ TRONG HỆ SIÊU TĨNH

Chuyển vị trong hệ siêu tĩnh được tính theo công thức Mohr, chẳng hạn khi sử dụng phép nhân biểu đồ Vêrêxaghin thì chuyển vị theo phương k sẽ là:

km M k M 

với M k và M là biểu đồ mô men uốn đơn vị và biểu đồ mô men uốn do tải trọng

gây ra trong hệ siêu tĩnh. Như thế, ta phải giải hai bài toán siêu tĩnh: Một bài toán để vẽ M và một bài toán để vẽ M k .

Tuy nhiên, ta có thể đơn giản hoá tính toán bằng nhận xét: chuyển vị trong hệ siêu tĩnh và trong hệ cơ bản phải giống như nhau, nên ta có thể tính chuyển vị trong hệ cơ bản.

km

k

M0M

M - biểu đồ mô men do tất cả các lực (gồm tải trọng và các lực ẩn số gây ra) trong hệ cơ bản, cũng chính là biểu đồ mô men của hệ siêu tĩnh đã cho.

M 0k - biểu đồ mô men uốn chỉ do lực bằng đơn vị theo phương k gây ra trong hệ

cơ bản, hệ cơ bản này không nhất thiết phải trùng với hệ cơ bản đã chọn khi tìm M .

CÂU HỎI ÔN TẬP CHƯƠNG 2

1. Thế nào là hệ thanh biến hình, hệ thanh bất biến hình, hệ thanh tĩnh định, hệ thanh siêu tĩnh. Cho ví dụ.

2. Nêu nội dung phương pháp lực để giải hệ thanh siêu tĩnh. Ý nghĩa của phương trình chính tắc.

3. Viết và giải thích các biểu thức tính hệ số tự do và số hạng tự do trong phương trình chính tắc.

4. Giải thích cách xác định biểu đồ ứng lực nói chung và biểu đồ mô men uốn nói riêng, của hệ siêu tĩnh sau khi đã có nghiệm của hệ phương trình chính tắc.

5. Nêu ưu điểm của việc chọn hệ cơ bản khi giải dầm liên tục theo phương trình ba mômen.

6. Nêu biện pháp đơn giản để tính chuyển vị trong hệ siêu tĩnh.

Chương 3

ỔN ĐỊNH CỦA THANH THẲNG CHỊU NÉN, UỐN

3.1. KHÁI NIỆM CHUNG

Các chương trước của bài giảng Cơ học 1 đã đề cập tới việc xác định trạng thái ứng suất, biến dạng, chuyển vị của thanh và đã đánh giá độ bền, độ cứng của thanh trong các trường hợp chịu lực. Tuy nhiên, thực tế cho thấy rằng: các điều kiện này nhiều khi cũng chưa đảm bảo đầy đủ khả năng làm việc bình thường của kết cấu. Cùng với việc phân tích độ bền, độ cứng các kỹ sư cần quan tâm đến độ ổn định của kết cấu.

Sơ đồ tính, tính chất vật liệu mà chúng ta đặt ra với kết cấu là những khái niệm tuyệt đối, lý tưởng. Trong thực tế, kết cấu còn chịu những yếu tố thực, những nhiễu động. Dưới ảnh hưởng của những nhiễu động này, kết cấu có thể có những biến dạng lệch khỏi sơ đồ tính ban đầu. Khi ngừng nhiễu động, kết cấu có thể quay trở lại hoặc không quay trở lại sơ đồ tính ban đầu.

Ta định nghĩa một cách khái quát: độ ổn định của kết cấu là khả năng duy trì, bảo toàn được dạng cân bằng ban đầu trước các nhiễu động có thể xảy ra.

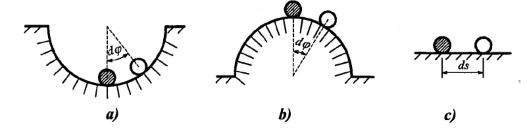
Hình 3.1: Các vị trí cân bằng của quả cầu

Để làm rò hơn khái niệm này, ta hãy xét sự ổn định của vật rắn qua sự cân bằng của quả cầu ở những vị trí khác nhau trên một bề mặt như trên hình 3.1: trên đáy lòm (độ cong dương), trên đỉnh lồi (độ cong âm) và trên mặt nằm ngang (độ cong bằng không). Những vị trí cân bằng này gọi là vị trí cân bằng ban đầu. Nếu cho quả cầu một xê dịch nhỏ đưa nó từ vị trí cân bằng ban đầu sang một vị trí lân cận mới, gọi là vị trí cân bằng nhiễu động, và sau đó ngừng nhiễu động thì ta dễ dàng nhận thấy:

- Trong trường hợp thứ nhất, trên hình 3.1a, quả cầu sẽ quay trở lại vị trí ban đầu. Vị trí cân bằng ban đầu là ổn định.

- Trong trường hợp thứ hai trên hình 3.1b, quả cầu sẽ không quay lại vị trí ban đầu mà tiếp tục chuyển động. Vị trí cân bằng ban đầu khi này là không ổn định.

- Trong trường hợp thứ ba trên hình 3.1c, quả cầu sẽ không quay trở lại vị trí ban đầu nhưng cũng không chuyển động xa hơn mà nằm ngay tại vị trí cân bằng nhiễu động. Vị trí cân bằng ban đầu là phiếm định.

Điều kiện để quả cầu có vị trí cân bằng ổn định là độ cong của bề mặt tựa k > 0. Hiện tượng tương tự cũng xảy ra đối với trạng thái cân bằng biến dạng của hệ

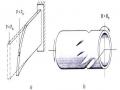
kết cấu. Để đơn giản, ta xét một thanh thẳng chịu nén đúng tâm bởi lực N như trên hình vẽ 3.2. Trong quá trình xem xét, ta sẽ tăng dần trị số của lực, bắt đầu từ 0. Trạng thái cân bằng ban đầu của thanh là dạng thẳng, thanh chỉ chịu nén đúng tâm. Gây ra cho thanh một nhiễu động, chẳng hạn bằng một lực ngang nhỏ R đủ đưa thanh ra khỏi vị trí cân bằng thẳng, thanh sẽ cong đi. Dạng cân bằng cong này gọi là trạng thái cân bằng nhiễu động. Nếu ngừng các nhiễu động, bỏ lực ngang R, ta nhận thấy sẽ xảy ra các khả năng sau:

- Khi giá trị lực nén N bé, chẳng hạn nhỏ hơn một trị số Nth nào đó, thanh sẽ thẳng trở lại. Trạng thái cân bằng của thanh là ổn định (hình 3.3a)

- Khi giá trị lực nén N lớn,vượt quá trị số Nth, thanh không thẳng trở lại mà tiếp tục cong thêm, xa dần trạng thái cân bằng ban đầu. Trạng thái cân bằng ban đầu của thanh, khi này, là trạng thái cân bằng không ổn định (hình 3.3c). Khi bị mất ổn định, thanh sẽ cong thêm, ngoài chịu nén thanh còn chịu uốn, ứng suất và biến dạng sẽ tăng lên dẫn đến thanh bị phá hủy.

- Tồn tại một trạng thái chuyển tiếp trung gian, khi lực nén N = Nth, sau khi bỏ nhiễu động, thanh không thẳng trở lại nhưng cũng không cong thêm. Thanh giữ nguyên trạng thái cân bằng nhiễu động (hình 3.3b). Trạng thái trung gian này được gọi là trạng thái cân bằng tới hạn. Trị số lực nén Nth tương ứng được gọi là lực nén tới hạn.

a) b) c)

N

Nth

N=Nth

N < N>Nth

Hình 3.2: Thanh thẳng chịu nén

Hình 3.3:Các dạng cân bằng của thanh

Cần lưu ý rằng nhiễu động luôn luôn tồn tại, sẵn có trong điều kiện thực của kết cấu. Đó là độ cong ban đầu của trục thanh khi chế tạo, là sự không đồng đều của tiết diện, là độ lệch tâm vốn có của lực nén, là những tác động ngẫu nhiên của tải trọng ngang…, là tất cả những yếu tố sai lệch thực tế không thể tránh khỏi so với điều kiện lý tưởng. Vì vậy, bài toán ổn định của thanh mang ý nghĩa thực tế rất lớn. Khi tính toán kết cấu, cần đảm bảo để thanh không bị mất ổn định. Đối với thanh chịu nén đúng tâm thì điều kiện này được biểu diễn bởi bất đẳng thức:

N Nth

Điều kiện ổn định nêu trên độc lập đối với các điều kiện bền và điều kiện cứng

Xem tất cả 91 trang.