Quan Hệ Độ Vòng - Lực Nén (Dạng Không Thứ Nguyên)

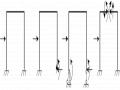
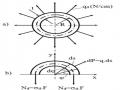
toán. Bằng phương pháp mặt cắt, ta xét thanh ở trạng thái biến dạng, ta tìm được trị số của mô men uốn

M Sy Rz F1z a

S F1 F2

y

R

1

y

F

S

Có thể bạn quan tâm!

• Hệ Siêu Tĩnh Đối Xứng Và Phản Xứng X 1 , X 2 , X 3 Là Nghiệm Của Phương Trình Chính Tắc:
• Diện Tích Và Hoành Độ Trọng Tâm Của Một Số Hình Phẳng
• Khái Niệm, Phương Trình Vi Phân Của Đường Đàn Hồi
• Bài Toán Kéo Vật Nặng Lên Cao Với Gia Tốc Không Đổi
• Sức bền vật liệu - 10
• Sức bền vật liệu - 11

Xem toàn bộ 91 trang tài liệu này.

R a M

z

Hình 3.9: Thanh chịu uốn ngang và uốn dọc đồng thời

Lượng Sy là mô men uốn do lực dọc; lượng trong móc vuông là mô men uốn chỉ do tải trọng ngang, ký hiệu là M và xác định bình thường như khi không có tải trọng dọc. Khi đó biểu thức của mô men uốn sẽ được viết tổng quát là:

M M Sy

(3.21)

Biểu thức (3.21) cho thấy nội lực không những phụ thuộc vào ngoại lực mà còn phụ thuộc vào biến dạng, đó là một đặc điểm của bài toán đang xét. Độ vòng được xác định theo phương trình vi phân đường đàn hồi:

y'' M

EI

Thay giá trị (3.21) vào (3.22), sau khi rút gọn ta có:

y'' k 2 y M x

EIx

(3.22)

(3.23)

Trong đó:

k 2 S

EIx

(3.24)

Giải phương trình vi phân cấp hai không thuần nhất (3.23) kết hợp các điều kiện biên ta tìm được độ vòng y, sau đó tính mô men uốn theo (3.21)

Nghiệm tổng quát của (3.23) sẽ là:

y'' y* y

Trong đó:

y* - là nghiệm tổng quát của phương trình thuần nhất

y C1cosz C2

sinz

y - là nghiệm riêng của phương trình có vế phải, phụ thuộc vào biểu thức cụ thể của mô men uốn ngang M , do đó, phụ thuộc vào dạng cụ thể của tải trọng ngang.

Để tránh những khó khăn chi tiết của từng bài toán riêng biệt, ta có thể giải bài

toán một cách gần đúng như sẽ trình bày dưới đây.

3.6.2. Biểu thức gần đúng của độ vòng

1. Thanh thẳng có liên kết khớp ở hai đầu

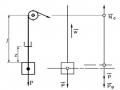
Giả thiết tải trọng ngang hướng về một phía và đối xứng qua tiết diện chính giữa nhịp như trên hình 3.10. Khi đó độ vòng cũng đối xứng, đạt cực trị f ở chính giữa nhịp và bằng không ở hai đầu.

F1

f

F1

l/2

l/2

Hình 3.10: Đường đàn hồi dạng đối xứng

Có thể chọn hàm độ vòng y thỏa mãn các điều kiện kể trên dưới dạng:

y f sin z

l

(i)

Độ vòng y , do tải trọng ngang cũng có thể viết dưới dạng tương tự:

y f sin z

l

(k)

Trị số độ vòng cực trị f tại chính giữa dầm do tải trọng ngang gây ra có thể tìm được bằng các phương pháp quen thuộc đã biết. Quan hệ giữa y và mô men uốn M vẫn được diễn tả băng phương trình vi phân của đường đàn hồi:



'' M

y

EIx

(1)

Thay (l) vào phương trình độ vòng (3.23) ta nhận được quan hệ:

y'' k 2 y y''

(3.25)

Thay thế các biểu thức độ vòng (i) và (k) vào (3.25), sau khi rút gọn ta được:

f f

1S

2 EIx 

l2 

Ký hiệu

NEuler



x

2 EI , biểu thức này có dạng công thức tính lực tới hạn Euler

l2

tương ứng với độ cứng chống uốn của mặt phẳng đang xét EIx thay cho độ cứng nhỏ nhất EImin

f f

1S

NEuler

(3.26)

Thay (3.26) vào (k), kết hợp với (l) ta có thể viết biểu thức độ vòng khi uốn ngang, uốn dọc đồng thời:

y y

1S

NEuler

(3.27)

y là độ vòng của dầm chỉ do tải trọng ngang, tìm được bằng các phương pháp quen thuộc đã biết.

Với các tải trọng ngang không đối xứng nhưng cùng hướng về một phía, ta vẫn

chấp nhận công thức (3.27) để tính độ vòng.

2. Thanh thẳng có liên kết khác ở hai đầu.

Khi thanh chịu uốn ngang, uốn dọc đồng thời có các kiểu kiên kết khác, ta cũng có thể dùng công thức () để tính độ vòng, trong đó biểu thức của lực Euler được điều chỉnh bằng hệ số ảnh hưởng liên kết  có giá trị như khi tính ổn định của thanh thẳng chịu nén đúng tâm.

NEuler

2 EI

x

l 2

(3.28)

3.6.3. Biểu thức gần đúng của mô men uốn

Sau khi xác định được độ vòng, ta tính mô men uốn theo (3.21):

M M Sy M S y

1S

NEuler

(3.29)

''

Tuy nhiên cũng có thể tính được mô men uốn bằng một phép tính gần đúng tiếp theo như sau:

- Từ phương trình vi phân đường đàn hồi, ta có quan hệ:

M x y'' M x y

- Lấy đạo hàm cấp 2 của y và y theo biểu thức gần đúng (i), (k), kết hợp với (3.26) ta nhận được:

2 f sin z

Ml l f 1

x 

M x 2 f sin z

f 1S

l l

NEuler



Như vậy, biểu thức tính mô men uốn M do uốn ngang và uốn dọc đồng thời được biểu thị theo mô men uốn M do uốn ngang:

M M xx 1SNEuler

(3.30)

Tính mô men uốn theo (3.30) đơn giản hơn tính theo (3.29) nhưng kém chính

xác hơn vì phải chấp nhận hai lần gần đúng.

3.6.4. Ứng suất và điều kiện bền.

Nội lực trên thanh chịu uốn ngang và uốn dọc đồng thời bao gồm lực dọc N=-S

và mô men uốn M.

Ứng suất pháp trên tiết diện thanh:

SM x y

A Ix

(3.31)

M x

Ứng suất pháp lớn nhất trên tiết diện chữ nhật, khi sử dụng công thức gần đúng thứ hai của mô men uốn, được viết là:

M x

SS

(3.32)

max

A Wx

A 

S

Wx 1N 

Euler 

Biểu thức (3.32) cho thấy khi tải trọng ngang và dọc tăng lên n lần thì ứng suất tăng lên lớn hơn n lần. Do đó điều kiện bền không thể viết theo ứng suất cho phép

0

max n

mà cần đưa hệ số an toàn vào tải trọng.

nM x

Khi này, điều kiện bền của thanh chịu uốn ngang và uốn dọc đồng thời, khi sử dụng công thức gần đúng thứ hai của mô men uốn, phải viết dưới dạng:

nS

A nS 0

N

Wx 1





Euler 

Ngoài ra, cần lưu ý kiểm tra ổn định của thanh trong mặt phẳng quán tính không chứa tải trọng ngang, là mặt phẳng xz .



S

A

Hệ số uốn dọc tìm ở bảng (3.1) theo trị số của độ mảnh xz của thanh trong mặt phẳng xz:

i

xzl

xz

y

3.7. THANH CÓ ĐỘ MẢNH LỚN CHỊU NÉN LỆCH TÂM

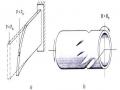
Thanh thẳng chịu nén lệch tâm là một trường hợp thường gặp trong thực tế vì độ lệch tâm của lực là không tránh khỏi. Khi thanh mềm, có độ mảnh lớn, chẳng hạn các kết cấu bằng kim loại, hiện tượng uốn dọc làm cho quan hệ chuyển vị - ngoại lực, quan hệ nội lực - ngoại lực trở thành các quan hệ phi tuyến, phức tạp như đã thấy từ các nghiên cứu ở trên. Ta khảo sát thêm trường hợp một thanh côngxôn chịu nén bới

lực F có độ lệch tâm e như hình 3.11 nhằm mục đích thiết lập mối quan hệ giữa lực nén F và độ lệch tâm e.

Mô men uốn tại tiết diện có toạ độ z:

M F(e y)

Phương trình vi phân của đường đàn hồi:

EIy'' F(e y)

Hay:

y'' k 2 y k 2 e 

Nghiệm tổng quát:

y C1 cos kz C2 sin kz e 

Điều kiện biên: khi z=0 thì y=y’=0;

Khi z=l thì y=

Từ hai điều kiện đầu: C1 + e +=0 ; kC2=0; ta có C2=0

Điều kiện thứ ba cho:

C1 cos kl e  0

Biểu thức độ vòng sẽ là:

y l  cos kz e

cos kl

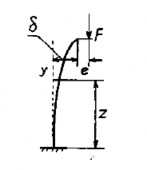
Hình 3.11: Thanh có độ mảnh lớn chịu nén lệch tâm

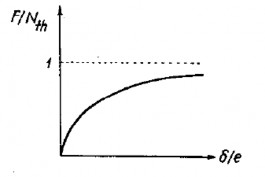
Hình 3.12: Quan hệ độ vòng - lực nén (dạng không thứ nguyên)

Đồ thị quan hệ giữa độ vòng của đầu tự do và lực nén F được trình bày trên hình

3.12. Đồ thị cho thấy khi lực nén tiến tới trị số lực tới hạn thì độ vòng tăng vô hạn, không phụ thuộc vào độ lệch tâm e. Do đó, bài toán Euler được coi như một trường hợp giới hạn.

3.8. ỔN ĐỊNH CỦA DẦM CHỊU UỐN

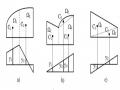
Khi trị số tải trọng ngang trên dầm chịu uốn phẳng vượt quá một trị số tới hạn thì dầm sẽ mất ổn định, ngoài biến dạng uốn dầm sẽ có biến dạng xoắn. Để đảm bảo dầm không mất ổn định, tải trọng ngang cần nhỏ hơn trị số tới hạn. Vì sự phức tạp của bài toán, trong mục này ta chỉ xét bài toán ổn định của dầm tiết diện chữ nhật chịu uốn bởi hai mômen M trong mặt phẳng yoz như hình 3.13a. Hai đầu dầm được liên kết sao cho tại liên kết độ vòng y theo phương y, độ vòng x theo phương x và góc xoắn tại tiết diện quanh trục z bằng không. Bài toán tìm mômen tới hạn được giải quyết theo quan điểm của Euler như đã được tiến hành với thanh thẳng chịu nén đúng tâm: tìm điều kiện để tồn tại một dạng cân bằng, khác với dạng cân bằng đã cho ban đầu.Ở đây dạng cân bằng ban đầu là dạng cân bằng chịu uốn, dạng cân bằng khác là dạng uốn và xoắn đồng thời.

Giả thiết mô men uốn M đạt giá trị tới hạn, ngoài biến dạng uốn, thanh còn có biến dạng xoắn như hình 3.13b. Tiết diện thanh có độ vòng y do mômen uốn Mx , độ vòng x do mômen uốn My và góc xoắn do mômen xoắn Mz. Trên hình vẽ các mômen

được biểu diễn bằng các vectơ mômen. Ta giả thiết mômen ngoại lực M vẫn nằm trong mặt phẳng ban đầu, nghĩa là vectơ mômen ngoại lực giữ phương không đổi; tương tự như giả thiết phương lực dọc N không đổi trong bài toán thanh chịu nén. Khi đó, từ điều kiện cân bằng vectơ mômen nội lực toàn phần trên tiết diện vẫn giữ phương không đổi. Vectơ mômen nội lực toàn phần được phân ra thành vectơ mômen xoắn và vectơ mômen uốn. Vectơ mômen xoắn có phương z của trục thanh sau biến dạng, vectơ mômen uốn có phương x và phương y của tiết diện sau biến dạng.

Xem các góc quay là nhỏ, có thể tính mômen uốn và mô men xoắn như sau:

* Theo hình 3.13c: mômen uốn quanh trục x là:

Mx M cosM

mô men xoắn:

M M sinMtgM dx Mx'

z dz

* Theo hình 3.13d: mô men uốn quanh trục y là:

M y MxtgM

Trong đó:  - góc xoắn của tiết diện đang xét;

 - góc nghiêng của trục thanh so với trục thanh trong mặt phẳng xz

tgdx

dz

Ký hiệu độ cứng khi uốn và khi xoắn của tiết diện lần lượt là EIx, EIy ,GIxo; ta có các quan hệ vi phân:

* Uốn trong mặt phẳng yz:

''

EIx y M x M

* Uốn trong mặt phẳng xz:

EI y x M M

''

y

* Xoắn:

GIxo

dM dz z

Mx'

Sau khi biến đổi ta được quan hệ:

xo

GI '' Mx'' M M 

EI

Đặt:

m2 

y

M 2

EI yGIxo

Ta tìm được giá trị của mô men uốn tới hạn như sau:

EI yGIxo



Mth l

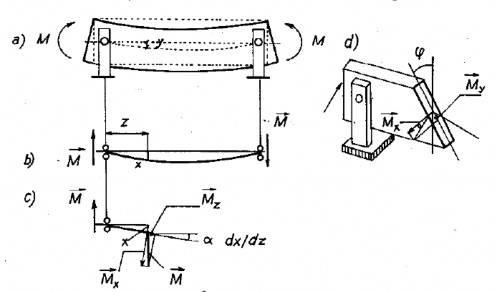
Hình 3.13: Ổn định của dầm chịu uốn thuần tuý

3.9. CÁC VÍ DỤ

Ví dụ 3.1

Tính lực tới hạn và ứng suất tới hạn của một cột làm bằng thép số 3 mặt cắt ngang hình chữ I số 22a. Cột có liên kết khớp hai đầu. Xét hai trường hợp:

a) Cột cao 3m.

b) Cột cao 2,5m. Biết E = 2,1.105 MN/m2

Bài giải:

Mặt cắt ngang hình chữ I số 22a có F = 32,4 cm2; iy = imin = 2,5 cm. Theo liên kết của thanh thì  = 1.

a) Khi cột cao 3m.

Độ mảnh  của thanh là:

l

imin

 1.3

0,025

 120

Ta đã biết với thép số 3 thì o = 100. Nên (12.5) để tính ứng suất tới hạn:

0

do vậy ta dùng công thức

th

2 E

2

 3,14 .2,1.10 

2 5

1202

143 MN / m2

Do đó lực tới hạn của thanh bằng:

6 4 3

Nth th .A 143.10 .32, 4.10 463.10 N 

b) Khi cột cao 2,25 m:

Độ mảnh  của cột bằng:

l

imin

 1.2,25  90 

0,025 o

Ta dùng công thức (12.8) để tính th. Biết a = 336 MN/m2; b = 1,47 MN/m2

2

4 3

th a b.336 1, 47.90 204 MN / m 

Khi đó:

Ví dụ 3.2

Nth th .A 204.32, 4.10 0,66.10 N 

Một thanh có chiều dài l=3m, một đầu ngàm, một đầu khớp. Hãy xác định lực tới hạn của thanh trong ba trường hợp sau đây:

a) Mặt cắt hình tròn bán kính R=4cm, vật liệu là gang xám có tl =178 MN/m2,

E=11,5.104 MN/m2

b) Mặt cắt hình tròn rỗng, bán kính ngoài R=3cm, bán kính trong r=2cm, vật liệu là đuyra có tl=180 MN/m2, E=7,1.104 MN/m2

c) Mặt cắt hình vuông cạnh 15  15cm, vật liệu bằng gỗ có tl=17 MN/m2,

E=104 MN/m2

Bài giải: