Sức bền vật liệu - 2

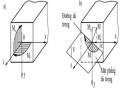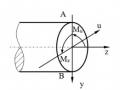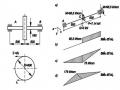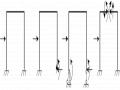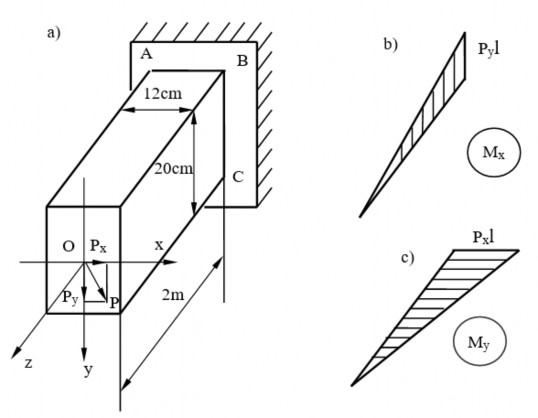
Hình 1.5: Hình ví dụ 1.1

Ta có ứng suất tại điểm A:

Py l

Px l

2, 08.200101, 2.2006

A IyA

I xA

Có thể bạn quan tâm!

• Sức bền vật liệu - 1
• Thanh Mặt Cắt Ngang Tròn Chịu Uốn Đồng Thời Xoắn
• Trục Chịu Uốn Và Xoắn Đồng Thời Các Biểu Đồ Nội Lực Được Biểu Diễn Trên Các Hình 1.22B, C, D. Thay Số Vào Ta Được:
• Hệ Siêu Tĩnh Đối Xứng Và Phản Xứng X 1 , X 2 , X 3 Là Nghiệm Của Phương Trình Chính Tắc:

Xem toàn bộ 91 trang tài liệu này.

8000 2880

x y

 0, 52  0, 50  1, 02 kN / cm2 

2

2

Tương tự, chúng ta tính được ứng suất tại các điểm B, C, D tương ứng là:

2

B 0, 02 kN / cm ,

Ví dụ 1.2:

C 1, 02 kN / cm ,

D 0, 02 kN / cm .

Cho dầm chịu lực như hình 1.6. Xác định số hiệu mặt cắt dầm thép chữ I, vị trí đường trung hoà.

Cho biết: P = 2400N; q = 4000N/m; l = 2m;= 300; [] =16000N/m2.

Bài giải:

Mặt cắt nguy hiểm tại ngàm có:

ql2

M x 

Pl.cos 12160(Nm)

2

M y Pl.sin 2400(Nm)

Thử lần thứ nhất ta lấy C = 4.

Vậy:

W M x CM y x 

 196(cm3 )

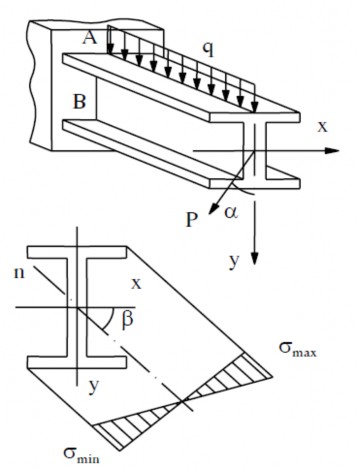
Hình 1.6: Hình ví dụ 1.2

Ta chọn mặt cắt chữ I số 20 có các giá trị nhỏ hơn và gần nhất Wx=184cm3; Wy=23,1cm3.

Thử lại:

max min

M x M y

 17000(N / cm2 )

Vì :

max

Wx Wy

max 



100% 

17000 16000

16000

100%  6, 2%  5%

Do đó ta lấy mặt cắt số 20a có Wx = 203cm3 , Wy = 28,2cm3

Khi đó:

M x M y

 14500(N / cm2 )

max

Wx Wy

Ứng suất nhỏ hơn:

max 

14500 16000



100% 

16000

9, 4%

Vì giữa thép có số hiệu 20 và 20a không còn số hiệu nào khác nên ta chọn dầm

thép có số hiệu 20a.

Xác định vị trí đường trung hoà. Tra bảng với I(20a) ta có Ix=2030cm4; Iy=155cm4’. Do đó tại mặt cắt ngàm, phương của đường trung hoà là :

Hay:

tgIx M y max

I y M x max

 68050

 2030 2400  2,58 15512160

1.3. THANH CHỊU UỐN ĐỒNG THỜI KÉO (NÉN)

1.3.1. Khái niệm

Thanh chịu uốn đồng thời kéo (nén) khi ứng lực trên tiết diện gồm lực dọc Nz, mô men uốn Mx, My hoặc lực dọc và một trong hai mô men uốn này (hình vẽ 1.7).

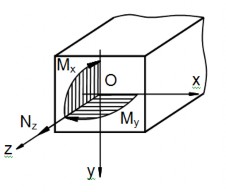
Hình 1.7: Thanh chịu uốn đồng thời kéo

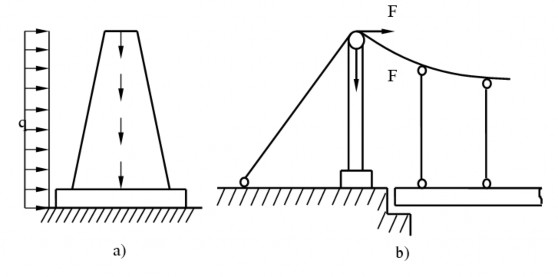
Hình 1.8: Ống khói và cột cầu treo chịu uốn đồng thời nén

Hoặc ví dụ đối với ống khói, trọng lượng cột gây nén còn tải trọng gió q gây uốn (hình 1.8a). Cột chống cầu treo khi chịu sức căng của dây treo không vuông góc với trục thanh thì lúc đó phân tích lực căng dây thành hai thành phần: thành phần F1 gây uốn, thành phần F2 gây nén (hình 1.8b).

1.3.2. Ứng suất pháp trên mặt cắt ngang

Ứng suất pháp tại một điểm trên MCN được xác định theo công thức:

z

Nz M x y M y x

(1.16)

A Ix I y

hoặc

Nz1



z A

M x

N i2

y M y

N i2



x 

(1.17)

z x z y 

Trong đó: A - diện tích MCN;

ix, iy - bán kính quán tính chính:

Ix

A

I y

A

ix ; iy 

Ix, Iy- mômen quán tính chính trung tâm của MCN;

x, y - toạ độ của điểm tính ứng suất.

M x

Ix

M y

I y

Công thức kỹ thuật có dạng:

Nz



y x

(1.18)

z A

Trong công thức trên các giá trị đều lấy giá trị tuyệt đối. Còn lấy dấu “+” hoặc “-” trước mỗi số hạng tuỳ theo lực dọc là kéo hay nén và các mômen uốn Mx, My gây ra ứng suất kéo hay nén ở điểm đang xét.

1.3.3. Vị trí đường trung hoà

Từ phương trình (1.18) ta có phương trình đường trung hoà là:

Nz M x

A Ix

y M y x  0

I y

(1.19)

hay:

1M x

N i2

y M y

N i2

x  0

(1.20)

z x z y

Đường trung hoà trong trường hợp thanh chịu kéo (nén) đồng thời uốn là một đường thẳng không đi qua trọng tâm của MCN như trong uốn xiên.

1.3.4. Biểu đồ ứng suất pháp trên MCN

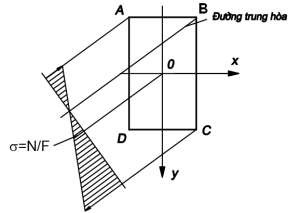
Hình 1.9: Biểu đồ phân bố ứng suất pháp trên MCN thanh chịu uốn đồng thời kéo (nén)

Tương tự như trong uốn xiên do mặt cắt ứng suất là phẳng, nên ứng suất pháp phân bố đều trên đường thẳng song song với đường trung hoà. Biểu đồ phân bố ứng suất được vẽ như hình 1.9.

1.3.5. Điều kiện bền

max

Điểm nguy hiểm là các điểm ở chu vi, xa đường trung hoà nhất về phía kéo hoặc phía nén. Trạng thái ứng suất của điểm nguy hiểm là trạng thái ứng suất đơn. Vậy điều kiện bền là :

- Đối với vật liệu dẻo:



(1.21)

M x

Ix

M y

I y

- Đối với vật liệu giòn: trong đó:





;

max k





min n

(1.22)

Nz



y x

(1.23)

max A

Nz

M x

Ix



y x

(1.24)

min A

M y

I y

xk, yk : là toạ độ của điểm chịu kéo cách xa đường trung hoà nhất.

xn, yn : là toạ độ của điểm chịu nén cách xa đường trung hoà nhất.

Nz

M x

M y

 Nếu MCN của thanh có dạng như trên hình 1.9 thì lí luận tương tự như trong uốn xiên ta có:

(1.25)

max

A Wx Wy

Nz

M x

M y

(1.26)

min

A Wx Wy

1.3.6. Khái niệm về lòi mặt cắt ngang

Trong các công trình xây dựng ta thường gặp những vật liệu chịu nén tốt nhưng chịu kéo kém như gạch, đá, bê tông.v.v... có khi hầu như vật liệu không chịu được kéo, như chỗ tiếp giáp giữa móng và nền đất. Vì vậy trong quá trình thiết kế những bộ phận công trình chịu nén lệch tâm, ta phải tìm vị trí của điểm đặt lực sao cho trên mặt cắt chỉ xuất hiện ứng suất nén, nghĩa là sao cho đường trung hoà không cắt qua mặt cắt ngang. Như vậy điểm đặt lực K phải nằm trong một miền nhất định bao quanh trọng tâm của mặt cắt. Miền diện tích ấy được gọi là lòi của mặt cắt ngang. Vậy lòi của mặt cắt ngang được xác định như sau:

- Xác định hệ trục quán tính chính trung tâm của mặt cắt ngang.

- Vẽ các đường trung hoà tiếp xúc với chu vi của mặt cắt ngang.

Vị trí các đường trung hoà này được xác định bởi toạ độ ai, bi tương ứng. Với mỗi một đường ta xác định được một điểm Ki(xi, yi) tương ứng theo công thức:

xki

i2

y ;

ai

yki

2

i

x

bi

(1.27)

Nối các điểm đặt Ki ta được chu vi của lòi (hình 1.10).

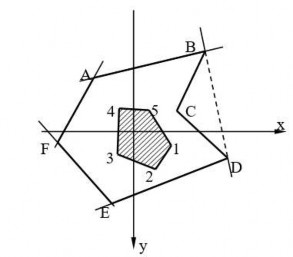
Hình 1.10: Chu vi của lòi mặt cắt ngang

Hình dáng và kích thước của lòi chỉ phụ thuộc vào hình dáng và kích thước mặt cắt ngang nó không phụ thuộc vào trị số nội lực đặt trên mặt cắt, do đó lòi có thể xem là một đặc trưng hình học của mặt cắt ngang.

Ta xét lòi của một số mặt cắt ngang thường gặp :

1) Hình chữ nhật

Do tính chất đối xứng của mặt cắt nên lòi cũng có tính đối xứng. Khi đường trung hoà tiếp xúc với AB:

a1 = ; b1 = -h/2.

Toạ độ điểm K1 (điểm 1) là:

xk 1

2

i

y

a

2

i

y



 0;

yk 1

2

i

x

b

h2 h

12. h 6 2

Tương tự cho đường trung hoà tiếp xúc với AD ta có

a2 d / 2,b2 , nên

xk 2 d / 6, yk 2  0.

Lần lượt cho đường trung hoà tiếp xúc với DC và CB ta xác định

được điểm 1' và 2'. Nối 1, 2, 1', 2' ta được lòi của mặt cắt ngang là hình thoi (hình 1.11).

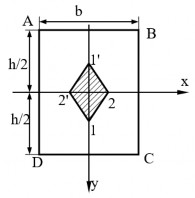
Hình 1.11: Lòi mặt cắt hình chữ nhật

2) Hình vành khăn

Lòi của hình vành khăn cũng là hình tròn (hình 1.12a) có bán kính

4

R

r ' R 12 , với r .

lòi

Trường hợp mặt cắt ngang là hình tròn đặc (hình 1.12b) thì bán kính của

r ' R .

4

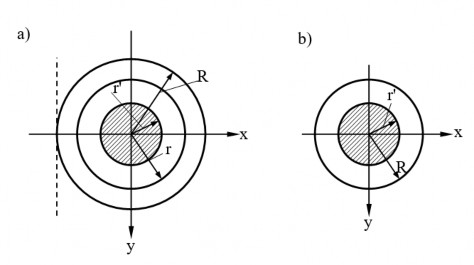
Hình 1.12: Lòi mặt cắt hình vành khăn

Ví dụ 1.3

Cho một thanh chịu lực như hình 1.13a. Tìm giá trị ứng suất max và min, vị trí đường trung hoà và vẽ biểu đồ phân bố ứng suất pháp trên mặt cắt nguy hiểm.

Cho: P1 = 160 kN; P2 = 4kN; P0 = 240kN; q=2kN/m; l=2m; b=12cm; h=16 cm.

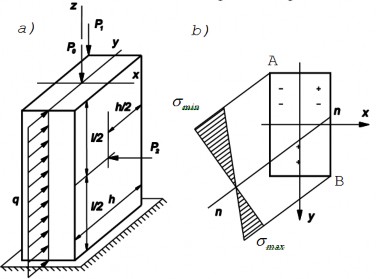
Hình 1.13: Hình ví dụ 1.3

Bài giải:

Mặt cắt nguy hiểm tại đầu ngàm. Vị trí đường trung hoà và biểu đồ ứng suất pháp được vẽ trên hình 1.13b.

Lực dọc:

NzP0P1240 160400(kN) .

Mômen uốn:

Ph ql2 2 4104

M 1 1608  1680kNcm

x 2 2 100 2

MP1bP2l 160 6  4102 1360kNcm

y 2 2

Giá trị ứng suất pháp lớn nhất và bé nhất theo (1.25), (1.26) là:

Nz

M x

M y

 4, 75kNcm

max

A Wx Wy

Nz

M x

M y

8, 91kNcm

min

A Wx Wy

Vị trí đường trung hoà: đường trung hoà cắt trục x và trục y tại các điểm:

x0 

2 h2

N i2

z y ;

M y

2

N i

z x

M

y0 

x

x 

x 





2 2 b2 2

trong đó:

i  21, 3 cm ;

12

i  12 cm

12

Nz  0 ;

M x  0 ;

M y  0 .

Khi thay bằng số ta được: x0 = 3,53 cm; y0 = 5,07 cm

1.4. THANH CHỊU KÉO (NÉN) LỆCH TÂM

1.4.1. Biểu thức ứng suất trên tiết diện