Thanh Mặt Cắt Ngang Tròn Chịu Uốn Đồng Thời Xoắn

Thanh chịu kéo lệch tâm khi ngoại lực tác dụng là các lực song song như không trùng với trục thanh. Đây là trường hợp chịu lực thường gặp ở những cột, thanh chịu kéo nén vì hầu như ta không thể đặt lực đúng trọng tâm tiết diện.

z

F M =F.y

z

N=F

x C My =F.xC

x x

C

y y

Có thể bạn quan tâm!

• Sức bền vật liệu - 1
• Sức bền vật liệu - 2
• Trục Chịu Uốn Và Xoắn Đồng Thời Các Biểu Đồ Nội Lực Được Biểu Diễn Trên Các Hình 1.22B, C, D. Thay Số Vào Ta Được:
• Hệ Siêu Tĩnh Đối Xứng Và Phản Xứng X 1 , X 2 , X 3 Là Nghiệm Của Phương Trình Chính Tắc:
• Diện Tích Và Hoành Độ Trọng Tâm Của Một Số Hình Phẳng

Xem toàn bộ 91 trang tài liệu này.

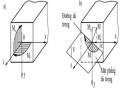
Hình 1.14: Kéo lệch tâm và các nội lực tương ứng

Nếu trên tiết diện có lực F đặt lệch tâm tại điểm C(xC, yC) như trên hình 1.14, bằng cách chuyển lực về trọng tâm tiết diện ta nhận được:

Lực dọc: Nz = F (1.28)

Các mô men uốn: Mx = F.yC (1.29)

My = F.xC (1.30)

Trong các biểu thức trên, F > 0 khi là lực kéo, xC, yC lấy dấu theo hệ toạ độ đã

chọn.

Nếu trên tiết diện có nhiều lực Fi đặt lệch tâm tại điểm tương ứng Ci (xCi, yCi),

thì giá trị lực F và điểm đặt C được tính theo kết quả của hợp lực

F Fi

(1.31)

C

x Fi xC

Fi

y Fi yC

C

Fi

(1.32)

Với các ứng lực theo (1.28),(1.29) ứng suất pháp trên tiết diện sẽ là:

N M x y M y x F FyC FxC y

(1.33)

A Ix I y A Ix I y

Suy ra:

F

yC y xC x 

A 1 r2 r2 

x y 

Trong đó rx, ry là các bán kính quán tính của tiết diện:

Ix

A

I y

A

rx  ; ry 

Ix

A

bh3

12bh

I y

A

hb3

12bh

* Với tiết diện hình chữ nhật b h:

rx 

h

; ry 

b

12

12

* Với tiết diện hình tròn rỗng có đường kính ngoài D và đường kính trong d:

Ix A

D4 14 

64D2 12 

D

4

12

rx 

Trong đó ký hiệu:

d

D

Bán kính quán tính của tiết diện các thép hình được tìm ở bảng tra theo số hiệu thép.

Qua biểu thức tính ứng suất (1.33), ta có những nhận xét sau:

+ Bài toán kéo (nén) lệch tâm có thể tính theo trường hợp kéo (nén) đúng tâm và uốn đồng thời và ngược lại bài toán kéo (nén) đúng tâm và uốn đồng thời cũng có thể tính theo bài toán kéo (nén) lệch tâm. Trong trường hợp sau, lực và điểm đặt sẽ được tính theo công thức:

F N ;

x M y ;

C N

y M x

C N

(1.34)

+ Định luật tác dụng tương hỗ: Ứng suất pháp tại điểm A do lực F đặt tại điểm C gây ra cũng bằng ứng suất pháp tại điểm C do lực F đặt tại điểm A gây ra.

+ Ứng suất pháp tại trọng tâm tiết diện do lực nén lệch tâm F gây ra không phụ thuộc vào vị trí điểm đặt lực và luôn bằng N/A.

1.4.2. Đường trung hoà khi kéo (nén) lệch tâm

Phương trình đường trung hoà tìm theo điều kiện = 0; từ (1.33), ta có:

1yC y xC x  0

r2 r2

x y

r2 r2

Nếu đặt:

a y

xC

b x

yC

( 1.35)

Phương trình đường trung hoà sẽ có dạng:

xy 1

a b

(1.36)

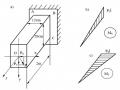
Hai thông số a và b là hoành độ và tung độ của giao điểm của đường trung hoà với trục hoành và với trục tung như chỉ trên hình 1.15

C

b

a

y

x

Hình 1.15: Vị trí đường trung hoà và điểm đặt lực C

Từ biểu thức (1.35) của a và b ta dễ dàng nhận thấy, ngoài những tính chất chung, đường trung hoà khi kéo (nén) lệch tâm còn có đặc điểm riêng sau:

1- Đường trung hoà không phụ thuộc giá trị của tải trọng mà chỉ phụ thuộc vào vị trí đặt tải trọng, đường trng hoà và điểm đặt lực luôn luôn nằm trong góc phần tư đối đỉnh của hệ trục toạ độ.

2- Điểm đặt lực nằm trên trục x thì đường trung hoà nằm song song trục y và ngược lại.

3- Khi điểm đặt di chuyển theo một đường thẳng thì đường trung hoà sẽ xoay quanh một điểm trên tiết diện.

Ví dụ 1.4

Một cột mặt cắt hình vuông bị nén lệch tâm trên trục y. Ứng suất tại điểm A bằng 200 N/cm2, tại B bằng không.

Hỏi tải trọng tác dụng lên cột, độ lệch tâm và ứng suất lớn nhất trên cột.

Bài giải:

Ta có: PD  PO và Mx = -P.yD Khi đó:

A

P P.yD

 200

(N / cm2 )

(1)

F Wx

Hình 1.16

P P.yD .y

 0 (N / cm2 )

(2)

x

B F IB

Từ (2) 

y Ix

B

D F.y

404  40

402.10.12 3

(cm)

P F.Wx .A

402.403.200

 32.104

(N )

yD .F Wx



 40 2 403 

Từ (1) 

6



.40 

3 6 

4 4

Ứng suất nén lớn nhất ở cột:



P P.yD

 32.10  32.10 .40 / 3 2

min C F W

402

403

600 (N / cm )

x

6

Ví dụ 1.5

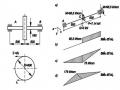
Một dụng cụ kẹp có dạng như hình vẽ 1.13. Cho: h=15mm, b=5mm, e=50mm. Tính mô men của ngẫu lực có thể đặt vào tay vặn để cho ứng suất lớn nhất ở thân giá không vượt quá ứng suất cho phép.

Cho []=160MN/m2. Bước của răng ốc vít = 1mm. Giả thiết bỏ qua các ảnh hưởng ma sát.

Bài giải:

Hình 1.13.

Quan hệ giữa mô men ngẫu lực đặt vào tay vặn và lực nén tác dụng vào chi tiết:

N 2M



Ứng suất ở thân chi tiết:

N16e2M16e

max bh h bh h 



bh

Hay:

M 

216e 

h 



Thay giá trị:

M  1600.0,1.0, 5.1, 5  9,1Ncm

 6.5 



2.3,1411, 5 

1.5. THANH CHỊU UỐN VÀ XOẮN ĐỒNG THỜI

Thanh chịu uốn đồng thời xoắn là thanh chịu lực sao cho trên mọi mặt cắt ngang

của nó chỉ có các thành phần nội lực là mô men uốn M x , M y và mô men xoắn M z .

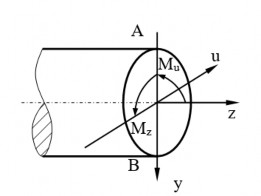
Hình 1.18: Thanh mặt cắt ngang tròn chịu uốn đồng thời xoắn

Bài toán này thường gặp trong các chi tiết máy. Ví dụ như một trục truyền lực

không phải chỉ chịu tác dụng mô men xoắn mà còn chịu tác dụng của mô men uốn do trọng lượng bản thân trục và trọng lượng của các chi tiết lắp trên trục.

1.5.1. Thanh có mặt cắt tròn

Hợp hai mô men uốn Mx và My ta được mô men uốn Mu:

M 2M 2

x

y

Mu 

Mô men uốn Mu cũng nằm trong mặt phẳng quán tính chính trung tâm nên hai

điểm có ứng suất pháp max ,min

là giao điểm của mặt phẳng tải trọng với chu vi mặt cắt

ngang (hình 1.18). Trị số của các ứng suất này:

M 2M 2

x

y

M

A B u(1.36)

max min

Wu Wu

trong đó Wu là mô men chống uốn của mặt cắt ngang đối với trục trung hoà u. Vì mặt cắt ngang là hình tròn nên:

Wu Wx Wy

Ứng suất tiếp lớn nhất do mô men xoắn gây ra ở các điểm thuộc chu vi của mặt cắt. Nó được tính theo công thức:

M z

(1.37)

W

max

p

Vậy tại các điểm A và B ngoài ứng suất pháp cực trị còn có ứng suất tiếp lớn nhất. Do đó, trạng thái ứng suất tại các điểm này là trạng thái ứng suất phẳng (hình 1.19). Điều kiện bền của các phân tố đó được viết theo các thuyết bền như sau:

min

max

B

max

max A

Hình 1.19

2  42

Theo thuyết bền ứng suất tiếp lớn nhất:

td 



2

Mu

M2

W 2 W 2



4z

x

p

Thay (1.36) và (1.37) vào ta có:

td 



Vì mặt cắt ngang là hình tròn nên Wp  2Wu  2Wx

nên:

td 



(1.38)

1

W

M 2M 2M 2

x

y z

x

Hay viết gọn lại:

td

Mtd

Wx



(1.39)

Trong đó:

Mtd 

M 2M 2M 2

x

y z

2 32

Theo thuyết bền thế năng biến đổi hình dáng lớn nhất:

td 



1

W

M M M

2

2

3

x

y

2

z

x

4

Thay (1.36) và (1.37) vào ta có:

td 



(1.40)

Hay viết gọn lại:

td

Mtd

Wx



(1.41)

Trong đó:

Mtd 

M M M

2

2

3

x

y

4

2

z

2  42

Nếu vật liệu giòn, ta sử dụng thuyết bền Mo. Khi đó điều kiện bền là:

td

112 2



Thay (1.36) và (1.37) vào ta có:

 11

1

M 2 M 2 M 2 

M 2M 2

x

y

W



x

td  2 2

k

x y z 

Trong đó:

0 0

k ,n

0



n

0

là ứng suất nguy hiểm khi kéo và ứng suất nguy hiểm khi nén.

1.5.2. Thanh có mặt cắt hình chữ nhật

Giả sử tại mặt cắt ngang nguy hiểm có các thành phần nội lực diễn như hình 1.20.

M x , M y , M z

biểu

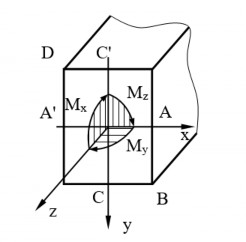
Hình 1.20: Thanh mặt cắt ngang chữ nhật chịu uốn đồng thời xoắn

Trong trường hợp đang xét thì ứng suất cực trị đạt được tại các điểm góc B, D của mặt cắt:



B

max



D

max



M x

M y

M y

Wx Wy

M x



Wx Wy

M Z

Mô men xoắn sinh ra ứng suất tiếp:



A

max



M Z

Wxoan

hb2

1 

max



M z

Wxoan

Vì trị số ứng suất ở các điểm A, B, C là khác nhau nên khó có thể xác định được điểm nào nguy hiểm hơn. Do đó, người ta thường kiểm tra bền cho cả ba phân tố ở ba điểm đó. Trạng thái ứng suất của các điểm được biểu diễn như hình 1.21.

- Đối với phân tố ở điểm B: phân tố ở trạng thái ứng suất đơn

max



M x

M y

Wx Wy

Chú ý với vật liệu giòn thì ta phải kiểm tra phân tố ở điểm D với điều kiện:

min



n

- Đối với điểm A: phân tố ở trạng thái ứng suất phẳng: Theo thuyết bền ứng suất tiếp lớn nhất:

2  42

M

 4z

y

2

M

2

Wy 

Wxoan 





A

td

Theo thuyết bền thế năng biến đổi hình dáng:

2  32

M

 3z

y

2

M

2

Wy 

Wxoan 





A

td

- Đối với điểm C: phân tố ở trạng thái ứng suất phẳng: Theo thuyết bền ứng suất tiếp lớn nhất:

2  42

M

 4z

y

2



M

2

Wy 

Wxoan 





C

td

Theo thuyết bền thế năng biến đổi hình dáng:

2  32

M

 3z

y

2

M

2

Wy 

Wxoan 





C

td

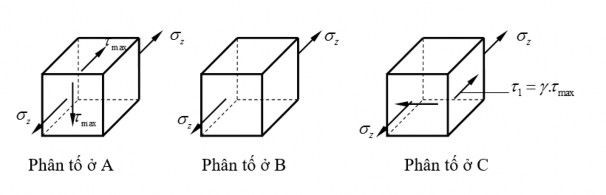
Hình 1.21: Trạng thái ứng suất tại các điểm A,B,C

Ví dụ 1.6

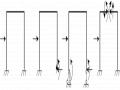
Một trục truyền bằng thép chịu lực như trên hình 1.22.

Trọng lượng Puli G = 3kN, công suất và số vòng quay của môtơ là: W = 50kW, n = 500vg/ph.

Kiểm tra bền trục theo thuyết bền thế năng biến đổi hình dạng biết

 12kN / cm2 .

Bài giải:

Sơ đồ chịu lực của trục biểu diễn trên hình 1.22a, trong đó:

n3,14500 52, 4rad / s

30 30

M W



 0,955103 Nm 95,5kNcm

Lực căng dây đai xác định theo điều kiện cân bằng của mômen xoắn: