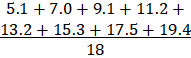Phát triển kiến thức và thực hành nghiệp vụ của giáo viên Toán tương lai để dạy học thống kê - 28

lớp về bảng tần số rời rạc, rồi tìm trung bình và trung vị theo đúng định nghĩa.

- Trung bình:

- Trung vị:

tần số ghép lớp

Lớp thu nhập

Tần số

4 – 6

1

6 – 8

0

8 – 10

1

10 – 12

2

12 – 14

2

14 – 16

3

16 – 18

5

18 – 20

4

Bảng phân bố tần số rời rạc

Giá trị Tần số

5 1

7 0

9 1

11 2

13 2

15 3

17 5

19 4

Giá trị trung bình

Vậy

Trung vị

Bảng dữ liệu này có diện tích là 18 phần, nên trung vị là vị trí mà nó chia đôi

diện tích (tức là mỗi bên 9 phần).

Vậy trung vị thu nhập là 16 triệu

 Ta có thể xác định được giá trị trung bình và trung vị dựa vào biểu đồ histogram

Lưu ý rằng: Khi xác định trung vị dựa vào biểu đồ thì trung vị là vị trí mà chia

đôi diện tích của biểu đồ

Hoạt động 4: Ước lượng giá trị trung bình, trung vị và mốt dựa vào hình dạng của biểu đồ

Mục tiêu: HS dựa vào hình dạng của biểu đồ để ước lượng giá trị trung bình, trung

vị và mốt dựa vào biểu đồ.

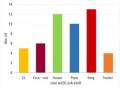
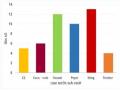
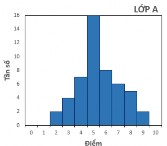
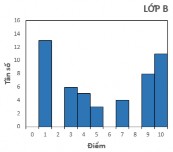
GV giao bài tập

Bài tập 3: : Trong buổi kiểm tra môn bóng rổ của một lớp học sinh, các học sinh thay phiên nhau ném bóng vào rổ. Số lần ném bóng thành công của mỗi học sinh được ghi lại trong biểu đồ sau.

Hãy so sánh số lần ném bóng thành công trung bình và trung vị

HS đọc yêu cầu bài tập Cả lớp hoạt động nhóm Một số nhóm đại diện trình bày kết quả.

Nhóm 1:

Trung bình:

Vậy

Trung vị: Bảng giá trị có các giá trị từ 0 đến

10. Do đó vị trí ở giữa

4. Mối quan hệ giữa trungbình, trung vị, mốt dựavào hình dạng của biểuđồ

Biểu đồ lệch trái Mốt > Trung vị > Trung bình

là 5

Vậy

: trung bình nhỏ hơn trung vị.

Nhóm 2:

Trung bình:

Vậy Trung vị:

Biểu đồ trên có 30 giá trị nên trung vị là trung bình cộng của 2 giá trị ở vị trí 15 và 16.

Giá trị ở vị trí 15 và 16 là 3

: trung vị nhỏ hơn trung bình.

Nhóm 3:

Trung bình:

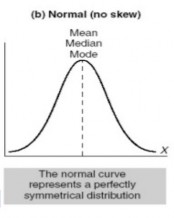
Biểu đồ đối xứng Mốt = Trung vị = Trung bình

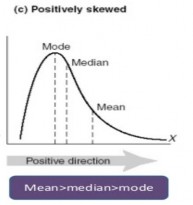
Biểu đồ lệch phải Mốt < Trung vị < Trung bình

Bài tập 3:

Biểu đồ trên lệch phải.Do đó mốt < trung vị < trung bình.

Trung vị:

Bảng giá trị có các giá trị từ 0 đến 10. Do đó vị trí ở giữa là 5

Vậy

: trung vị bằng trung bình.

HS suy nghĩ trả lời Biểu đồ trên lệch phải. Do đó mốt < trung vị < trung bình.

C. HOẠT ĐỘNG LUYỆN TẬP

Mục tiêu: giúp HS áp dụng được các kiến thức để làm một số bài tập

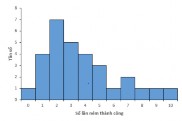
GV chiếu bài tập

Bài 1: (B-18) (Biểu đồ Histogram) Một nghiên cứu đã được thực hiện để kiểm tra mức sống của các gia đình điển hình ở Knoxville. Biểu đồ sau đây cho thấy sự phân phối thu nhập gia đình cho những người ở thị trấn Knoxvill. Phát biểu nào sau đây có khả năng là một so sánh chính xác về thu nhập trung bình và gia đình trung vị ở Knoxville?

i. Thu nhập trung bình thấp hơn thu nhập trung vị.

ii. Thu nhập trung bình bằng thu nhập trung vị.

iii. Thu nhập trung bình lớn hơn thu nhập trung vị.

iv. Không thể xác định số đo nào lớn hơn từ biểu đồ đã cho.

Hoạt động

của HS

Nội dung

A. Hoạt động khởi động ( 7 phút)

Mục tiêu: Nhắc lại và củng cố các kiến thức về số trung bình, số trung vị và ý nghĩa của chúng.

HS lên bảng chọn bao lì xì và trả lời câu hỏi.

B. Hoạt động hình thành kiến thức

Hoạt động 1: Phương sai (15 phút)

Mục tiêu: Giúp học sinh nắm được công thức tính phương sai.

Phương pháp: Hoạt động cá nhân, hoạt động cặp đôi.

1. Phương sai

- Công thức tính phương sai:

n .(x x )2 n .(x x )2

s2 1 1 k k

N

f .(x x )2 f .(x x)2

1 1 k k

Trong đó: ni , fi lần lượt là tần số, tần suất của giá trị xi ; N là số các số liệu thống

kê; x là số trung bình của mẫu số liệu đã cho.

- Trong trường hợp bảng phân bố tần số, tần suất ghép lớp

n .(c x )2 n .(c x )2

s2 1 1 k k

N

f .(c x )2 f .(c x)2

1 1 k k

Trong đó, cilà giá trị đại diện của lớp thứ i .

* Chú ý:

- Khi hai mẫu số liệu có cùng đơn vị đo và có giá trị trung bình bằng hoặc xấp xỉ nhau, nếu phương sai của mẫu số liệu (so với số trung bình) càng bé thì độ phân