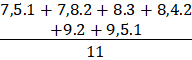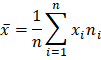Điểm Trung Bình Của Các Em Học Sinh Lớp 10A Trong Học Kì 1 Được Ghi Lại Trong Bảng Sau:

[0;5.0)

[5.0;6.5)

[6.5;8.0)

[8.0;10.0)

Tần số

0

6

19

15

Yếu

Trung Bình

Khá

Giỏi

Tần số

1

6

18

15

Hoạt động của HS

Nội dung ghi bài

A.HOẠT ĐỘNG KHỞI ĐỘNG

Mục tiêu: Ôn lại cách tìm giá trị trung bình, trung vị và mốt đã được học ở Đại số 10

Nội dung: Đưa ra một số bài tập và yêu cầu học sinh tìm trung bình, trung vị và mốt

-HS theo dõi

-HS đọc yêu cầu của VD1

HS trả lời: Để tìm trung bình, ta cộng tất cả giá trị các phần tử của dãy số lại rồi chia cho tổng số phần tử

HS trả lời: Để tính trung vị, đầu tiên ta sắp xếp các giá trị của dữ liệu theo thứ tự từ nhỏ đến lớn.

Nếu số phần tử của dãy số là lẻ thì trung vị là số chính giữa.

Nếu số phần tử của dãy số là chẵn thì trung vị là trung bình cộng của 2 số ở giữa.

HS đứng tại chỗ sắp xếp dãy số liệu

10, 13, 14, 15, 16, 17,

VD1: Cho số liệu về tuổi các học viên trong một lớp học tiếng Anh như sau: 10, 15, 13, 17, 18, 65, 20, 19,

22, 16, 21, 14

Hãy tìm trung bình và trung vị của dãy số liệu trên.

Giải

- Trung bình:

= 20,83

- Trung vị:

Sắp xếp các giá trị theo thứ tự từ nhỏ đến lớn:

10, 13, 14, 15, 16, 17, 18,

19, 20, 21, 22, 65

Ta nhận thấy, ở đây có 12 giá trị (quan sát), nên trung vị của dãy số này là trung bình cộng của 2 số ở giữa, đó là các giá trị thứ sáu và

thứ bảy.

18, 19, 20, 21, 22, 65

Dãy trên có 12 giá trị nên trung vị là trung bình cộng của giá trị thứ 6 và thứ 7

HS đọc đề

Điểm trung bình của học sinh là 8,3

Trung vị là 8,0

Đối với trung bình, ta nhân giá trị với tần số tương ứng, rồi cộng các kết quả và chia cho số giá trị

Đối với trung vị: Vì bảng có 11 giá trị nên trung vị là giá trị thứ 6 chính là 8,0

HS trả lời: Mốt là 3 HS tự đọc yêu cầu của VD3

HS trả lời: Chuyển bảng phân bố tần số ghép lớp

Trung vị: (17+18) / 2 =

17,5

VD2:

Điểm trung bình:

Trung vị:

Vì N = 11 nên trung vị của bảng này là giá trị ở vị trí thứ 6

Giá trị ở vị trí thứ 6 là 8,0

Vậy trung vị là 8,0

Mốt: M0 = 3

VD3: Trong một trường THPT, để tìm hiểu tình hình học Toán của lớp 10A, người ta cho lớp đó

m

7,5

7,8

8,0

8,4

9,0

số

1

2

3

2

2

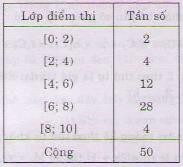
Hãy tính điểm trung bình của học sinh. Tìm trung vị và mốt của bảng trên.

?Một bạn giúp cô tìm điểm trung bình của học sinh và trung vị

? Em hãy trình bày cách tìm trung bình và trung vị đối với bảng số liệu này cho cả lớp lắng nghe

?Mốt của bảng số liệu trên là gì?

VD3: Trong một trường THPT, để tìm hiểu tình hình học Toán của lớp 10A, người ta cho lớp đó làm bài thi môn Toán theo cùng một đề thi và lập được bảng phân bố tần số ghép lớp sau đây

thành bảng phân bố tần số rời rạc rồi tìm trung bình và trung vị như ở VD2

HS trả lời: Tìm các giá trị đại diện cho mỗi lớp là trung bình cộng của 2 đầu mút của lớp tương ứng, và giữ nguyên tần số

HS trả lời: Các giá trị đại diện là 1; 3; 5; 7; 9. HS trả lời:

Trung bình: Trung vị:

làm bài thi môn Toán theo cùng một đề thi và lập được bảng phân bố tần số ghép lớp sau đây

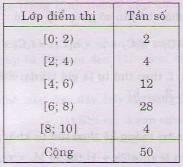
Giải

Bảng phân bố tần số rời rạc

Giá

trị

1

3

5

7

9

Tần

số

2

4

12

28

4

Trung bình:

Trung vị:

Ta thấy có 50 giá trị, nên trung vị là trung bình cộng của giá trị ở vị trí 25 và 26. Giá trị ở vị trí 25 là 7

Giá trị ở vị trí 26 là 7

Vậy trung vị là 7

B.HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

Hoạt động 1: Nhắc lại khái niệm và ý nghĩa của các giá trị trung bình, trung vị và mốt.

Mục tiêu: HS nhớ lại được những kiến thức đã học.

Nội dung: Đưa ra các phần lí thuyết và có ví dụ ở mức độ nhận biết và thông hiểu.

GV lần lượt nhắc lại khái niệm của các giá trị trị trung bình, trung vị và mốt.

- Giá trị trung bình:

- Đối với dãy số liệu rời rạc, công thức tính giá trị trung bình như thế nào?

- Đối với bảng tần số rời rạc, công thức tính giá trị trung bình là gì?

- Giá trị trung vị:

?Một bạn nhắc lại giúp cô cách tìm trung vị của một dãy số

- Mốt: Mốt Mo là giá trị có tần số lớn nhất trong bảng phân bố tần số.

Nếu trong bảng phân bố tần số có hai giá trị có tần số bằng nhau và lớn hơn tần số của các giá trị khác thì ta có hai giá trị đó là hai mốt

- Ý nghĩa của giá trị

HS suy nghĩ, trả lời: Lấy tổng các giá trị chia cho số giá trị.

HS trả lời: Tìm tích của mỗi giá trị và tần số tương ứng, rồi lấy tổng các kết quả đó chia cho tổng số phần tử.

-HS nêu cách tìm trung vị

HS trả lời: Giá trị trung bình và trung vị được lấy làm giá trị đại diện cho tập dữ liệu

HS suy nghĩ nhưng chưa trả lời được

1.Nhắc lại kiến thức

- Giá trị trung bình:

- Giá trị trung bình của một dãy số được

tính bởi công thức:

-Khi cho bảng phân bố tần số rời rạc

Giá

trị

…

Tần

số

…

Giá trị trung bình được tính bằng công thức

- Trung vị:

Số trung vị Me của một dãy gồm n số liệu thống kê được sắp thứ tự không

giảm (hoặc không tăng) là

-Số đứng giữa dãy (số hạng thứ ), nếu n lẻ.

-Trung bình cộng của hai

số đứng giữa dãy (số hạng thứ và ), nếu n chẵn.

- Mốt: Mốt Mo là giá trị có tần số lớn nhất trong bảng phân bố tần số.

Nếu trong bảng phân bố tần số có hai giá trị có tần số bằng nhau và lớn hơn tần số của các giá trị khác thì ta có hai giá trị đó là hai mốt.

- Ý nghĩa của giá trị trung bình và giá trị trung bình

Cả hai đại lượng này đều nhằm mục đích đo lường xu hướng tập trung của tập dữ liệu

Chú ý: Đối với dữ liệu có giá trị chênh lệch với các giá trị còn lại một cách bất thường (còn gọi giá trị ngoại lai), giá trị trung bình không thể đại diện thể hiện sự đặc trưng của dãy.

Khi đó giá trị trung vị lại

thể hiện đặc trưng của dãy tốt hơn.

Hoạt động 2: Tìm giá trị trung bình và trung vị thể hiện ở biểu đồ giá trị định tính

Mục tiêu: HS nắm được ở biểu đồ định tính, không thể xác định được giá trị trung

bình và trung vị

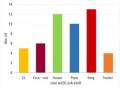
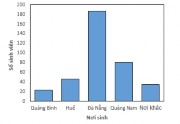
-GV đưa ra bài tập:

Bài tập 1: Biểu đồ sau đây cho thấy nơi sinh của các sinh viên trong một khóa học giới thiệu về thống kê

Hãy xác định trung vị. GV giải thích:

- Ta đã biết trung vị là giá trị ở giữa của dãy số liệu.

- Biểu đồ trên gồm các giá trị định tính, do đó, ta không thể tìm được trung vị.

GV nhấn mạnh lại kiến

thức

HS suy nghĩ trả lời

HS A: Trung vị là Đà Nẵng

HS B: Cần thêm dữ kiện mới có thể tìm ra trung vị

HS C: Không thể tìm ra trung vị

HS D: Trung vị là Huế

2.Biểu đồ giá trị định tínhĐối với biểu đồ gồm các giá trị định tính, ta không thể tìm được trung bình và

trung vị.

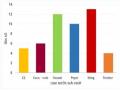
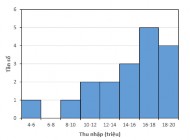
GV đưa ra bài tập

Bài tập 2: Một nghiên cứu đã được thực hiện để kiểm tra mức sống của các gia đình trong một tổ dân phố. Biểu đồ sau cho thấy sự phân phối thu nhập gia đình của những người trong tổ dân phố.

Hãy tìm trung vị thu nhập của các hộ dân trong tổ dân phố đó

GV phân tích câu trả lời của HS và chốt lại:

Trong biểu đồ tổ chức, diện tích các hình chữ nhật sẽ tỉ lệ với tần số (tần suất) lớp ghép. Do đó, khi xem xét phân bố dữ liệu, người ta dựa trên diện tích các hình chữ nhật chứ không phải

-HS suy nghĩ và trả lời

HS A: Trung vị của thu nhập là 12 triệu vì trong dãy giá trị thu nhập, 12 là giá trị chính giữa.

HS B: Trung vị của thu nhập là khoảng từ 12 đến 14 triệu vì trong biểu đồ trên có 8 cột, cột 12-14 đứng vị trí ở giữa.

HS C: Trung vị của thu nhập là 16 triệu vì tại giá trị 16 ta thấy nó chia đôi dữ liệu.

- Từ biểu đồ, ta có thể lập được bảng phân bố tần số ghép lớp

- Ta cần chuyển bảng

phân bố tần số ghép

3. Tìm trung bình, trungvị dựa vào biểu đồhistogram:

Lưu ý: Trong biểu đồ tổ chức, diện tích các hình chữ nhật sẽ tỉ lệ với tần số (tần suất) lớp ghép. Do đó, khi xem xét phân bố dữ liệu, người ta dựa trên diện tích các hình chữ nhật chứ không phải dựa trên chiều cao.

Vì vậy trung vị trong trường hợp này là vị trí chia đôi diện tích của biểu đồ.

Nhìn trên biểu đồ ta thấy, vị trí 16 chia đôi diện tích của biểu đồ.

Vậy trung vị thu nhập của các hộ dân trong tổ dân phố đó là 16 triệu.

 Hãy tính trung bình và trung vị thu nhập của các hộ dân trong tổ dân phố đó.

Giải

Từ biểu đồ, ta có phân bố