Phát triển kiến thức và thực hành nghiệp vụ của giáo viên Toán tương lai để dạy học thống kê

PHỤ LỤC 2C

THANG ĐÁNH GIÁ PHIẾU HỌC TẬP 3

Bài tập 1.

1) Anh (Chị) hiểu như thế nào về độ phân tán (độ biến thiên) của một chuỗi dữ liệu thống kê?

Độ phân tán (Dispersion) là một thuật ngữ thống kê mô tả kích thước của phân phối các giá trị dự kiến cho một biến cụ thể. Độ phân tán có thể được đo bằng các chỉ số thống kê khác nhau, chẳng hạn như khoảng giá trị, phương sai và độ lệch chuẩn.

2) Theo anh (chị) những tham số thống kê nào có thể dùng để mô tả độ phân tán của dữ liệu thống kê? Giải thích rõ.

Độ phân tán (độ biến thiên) có thể được xác định thông qua các tham số thông kê như: khoảng biến thiên (Range), Độ lệch tuyệt đối trung bình (Mean Absolute Deviation), Phương sai (Variance), Độ lệch chuẩn (Standard Deviation), Hệ số biến thiên (Coefficient of Variation).

• Khoảng biến thiên (Range) trong thống kê, là một đại lượng mô tả mức độ phân tán của dữ liệu. Khoảng biến thiên được tính bằng cách lấy giá trị quan sát lớn nhất trừ đi giá trị quan sát nhỏ nhất.

Công thức:

R Xmax Xmin

X max : giá trị lớn nhất của dãy dữ liệu

X min : giá trị nhỏ nhất của dãy dữ liệu

• Độ lệch tuyệt đối trung bình (Mean Absolute Deviation): là trung bình số học của các độ lệch tuyệt đối giữa các lượng biến với số trung bình.

xi x ni

Công thức:

x : giá trị trung bình

n : tổng số biến

d i1

xi : giá trị của biến thứ ni

• Phương sai (Variance) của một biến ngẫu nhiên là một độ đo sự phân tán thống kê của biến đó, nó hàm ý các giá trị của biến đó thường ở cách giá trị kì vọng bao xa.

Công thức:

s21mn x2nx 2

i i

n i1 

• Độ lệch chuẩn (Standard Deviation) là một đại lượng thống kê mô tả dùng để đo mức độ phân tán của một tập dữ liệu đã được lập thành bảng tần số.

1

i 1



n x nx

i i







Công thức: s 

Khi hai tập dữ liệu có cùng giá trị trung bình cộng, tập nào có độ lệch chuẩn lớn hơn là tập có dữ liệu biến thiên nhiều hơn.

• Hệ số biến thiên (Coefficient of Variation) là một đại lượng thống kê mô tả dùng để đo mức độ biến động của tương đối của những tập hợp dữ liệu có giá trị bình quân khác nhau. Hệ số này được tính bằng cách lấy độ lệch chuẩn chia cho giá trị trung bình. Giữa 2 tập hợp dữ liệu, tập nào có hệ số biến thiên lớn hơn là tập có mức độ biến động lớn hơn. Nhược điểm của hệ số biến thiên khi dùng để đo mức độ biến động là nếu giá trị bình quân gần 0 thì chỉ một biến động nhỏ của giá trị bình quân cũng có thể khiến cho hệ số này thay đổi lớn. Ưu điểm của nó là có thể dùng để so sánh mức độ biến động của 2 tập dữ liệu có giá trị bình quân khác nhau.

Một quy tắc dựa trên thực nghiệm (rule of thumb) được áp dụng khi đánh giá mức độ biến động của riêng một tập dữ liệu là nếu hệ số biến thiên nhỏ hơn 1 thì tập dao động nhỏ, nếu lớn hơn 1 thì tập dao động lớn.

Công thức: Hệ số biến thiên = Độ lệch chuẩn / Giá trị trung bình

CV 



Ở chương trình phổ thông, khi xét độ phân tán của dữ liệu người ta thường dùng các giá trị như khoảng biến thiên, phương sai và độ lệch chuẩn.

Bài tập 2:

1) Dựa vào đặc điểm của biểu đồ, hãy cho biết lượng mưa ở vùng nào có độ phân tán lớn hơn? Giải thích.

Trả lời:

Hai biểu đồ cho là biểu đồ cột, trục tung biểu diễn lượng mưa của các tháng. Độ phân tán được đánh giá bởi độ lệch (độ lệch chuẩn) giữa các cột so với lượng mưa trung bình hàng tháng. Khi độ lệch (độ lệch chuẩn) giữa các cột dữ liệu càng nhiều thì độ phân tán của dữ liệu càng lớn.

Vì vậy biểu đồ của vùng B sẽ có độ phân tán lớn hơn hơn vùng A.

2) Hãy đánh giá tính đúng/sai của các câu trả lời trên và giải thích tại sao đúng/sai.

HS2 đúng.

Học sinh

Đúng/Sai	Giải thích
HS1	S	Vì độ phân tán không phải được đánh giá bởi lượng mưa của các tháng mà phụ thuộc vào sự chênh lệch lượng mưa của các tháng với giá trị trung bình.
HS2	Đ	Vì các cột của vùng B có độ chênh lệch so với giá trị trung bình nhiều hơn vùng A nên vùng B sẽ có độ lệch chuẩn lớn hơn vùng A độ phân tán vùng B lớn hơn vùng A
HS3	S	Giá trị trung bình của dữ liệu không đánh giá được độ phân tán của dữ liệu
HS4	S	Mặc dù biểu đồ không biểu diễn số liệu cụ thể lượng mưa từng tháng nhưng chúng ta vẫn có thể so sánh độ phân tán của dữ liệu ở hai biểu đồ dựa vào loại biểu đồ và

Có thể bạn quan tâm!

Xem toàn bộ 277 trang tài liệu này.

Thang đánh giá bài tập 2.2

Mã số

Sự miêu tả

Xác định chính xác tính đúng/sai và giải thích rõ ràng cho câu trả lời

của cả bốn HS.

Xác định chính xác tính đúng/sai nhưng chỉ đưa ra lời giải thích cho

câu trả lời đúng ba trong bốn HS trong đó có câu trả lời đúng của HS2.

(i) Xác định tính đúng/sai chính xác của 4 HS nhưng chỉ giải thích đúng 2 trong 4 HS.

(ii) Xác định tính đúng/sai không chính xác (không xác định được câu trả lời đúng là của HS2) nhưng có đưa ra lời giải thích đúng cho câu trả

lời của hai trong bốn HS.

(i) Xác định tính đúng/sai không chính xác và chỉ đưa ra lời giải thích đúng câu trả lời của một trong bốn HS.

(ii) Xác định tính đúng/sai chính xác

Không xác định được tính đúng/sai và giải thích sai, không có yếu tố toán

học phù hợp trong câu trả lời hoặc không đưa ra bất kì phản hồi nào.

3) Hãy dự đoán xem lí do nào mà mỗi học sinh đã đưa ra câu trả lời như trong câu hỏi 2) ở trên.

Học sinh

Dự đoán lí do đưa ra các câu trả lời của học sinh
HS1	HS chưa nắm được khái niệm độ phân tán và cho rằng số tháng có lượng mưa nhiều hơn thì sẽ có độ phân tán nhiều hơn nên cho rằng lượng mưa vùng A có độ phân tán nhiều hơn vùng B.
HS2	HS nắm được khái niệm độ phân tán và biến so sánh độ phân tán dựa vào hình dạng phân bố của biểu đồ cột.
HS3	HS chưa nắm được khái niệm độ phân tán nên chỉ dựa vào giá trị trung bình bằng nhau mà kết luận độ phân tán lượng mưa của 2 vùng là như nhau.
HS4	HS nghĩ rằng phải có số liệu cụ thể để tính toán thì mới so sánh được. HS chưa biết cách so sánh độ phân tán dựa vào hình dáng phân bố của biểu đồ cột.

Thang đánh giá bài tập 2.3

Mã số

Sự miêu tả
4	Đưa ra những dự đoán hợp lí, rõ ràng cho câu trả lời của cả 4 HS.
3	Đưa ra dự đoán hợp lí, rõ ràng cho 3 trong 4 câu trả lời của các HS.
2	Đưa ra dự đoán hợp lí, rõ ràng cho 2 trong 4 câu trả lời của các HS.
1	Chỉ đưa ra dự đoán đúng cho câu trả lời của 1 HS.
0	Đưa ra các câu trả lời không có ý nghĩa hoặc không đưa ra bất kì phản hồi nào.

4) Theo anh (chị), học sinh THPT sẽ gặp những khó khăn hay sai lầm gì khi so sánh độ phân tán của dữ liệu được trình bày dưới dạng biểu đồ cột như Bài tập 2 này (dự đoán ít nhất ba khó khăn/sai lầm và lí giải).

STT

Khó khăn, sai lầm của HS khi làm bài tập 2.1
1	HS không nắm được khái niệm độ phân tán và không biết được độ phân tán được đánh giá thông qua những tham số nào.
2	HS không xác định được loại biểu đồ và không biết cách đọc thông tin trên biểu đồ.
3	HS mắc sai lầm cho rằng độ phân tán được so sánh thông qua giá trị trung bình và cho rằng độ phân tán của dữ liệu là như nhau nếu chúng có giá trị trung bình bằng nhau. (Hiểu nhầm ĐBT là GTTB)
4	HS chỉ biết so sánh độ phân tán dựa vào việc tính toán giá trị của các tham số thống kê chứ chưa biết dựa vào hình dáng của biểu đồ cột để so sánh độ phân tán của dữ liệu nên: 4A + Khi biểu đồ không cho giá trị các cột dữ liệu thì HS cho rằng biểu đồ không đủ dữ liệu để tính toán nên không so sánh được độ phân tán. 4B + HS thiếu kĩ năng phân tích biểu đồ, hình dáng của biểu đồ nên không thể so sánh được độ phân tán dữ liệu giữa các biểu đồ.
5	HS mắc sai lầm cho rằng độ phân tán của dữ liệu phụ thuộc vào chiều cao của cột giá trị. Nếu chiều cao của cột giá trị càng lớn thì độ phân tán càng cao và ngược lại chiều cao của các cột thấp thì độ phân tán của dữ liệu càng thấp.
6	HS sai lầm có thể sẽ hiểu độ phân tán là độ chênh lệch giữa các đơn vị với nhau nên sẽ đi so sánh lượng mưa giữa mỗi tháng với nhau.
7	7A: Không hiểu đề bài do không có kiến thức. 7B: Chưa biết tính toán, thiết lập các mối quan hệ giữa các đại lượng để đưa ra so sánh và nhận xét.

5) Giả sử bạn cần dạy về độ phân tán của dữ liệu thống kê được cho dưới dạng biểu đồ cột. Hãy đưa ra ít nhất ba chỉ dẫn hoặc lưu ý cụ thể để giúp học sinh THPT xác định đúng độ phân tán của dữ liệu dựa trên đặc điểm hình dạng của biểu đồ cột (mà không cần phải thực hiện các phép tính).

STT

Chỉ dẫn, lưu ý giúp HS xác định độ phân tán của dữ liệu trên biểu

đồ cột

Nêu khái niệm độ phân tán và những tham số thống kê để mô tả độ phân tán (ở phổ thông thường sử dụng các tham số như giá trị trung

bình, phương sai và độ lệch chuẩn để xét độ phân tán của dữ liệu).

Khi hai tập dữ liệu có cùng giá trị trung bình cộng, tập nào có độ lệch chuẩn lớn hơn là tập dữ liệu có độ phân tán nhiều hơn. Vì vậy, trên biểu đồ ta so sánh giá trị của các cột với giá trị trung bình, nếu mức độ chênh lệch giá trị dữ liệu của biểu đồ nào lớn hơn thì sẽ có độ phân tán lớn

hơn.

Dựa vào hình dạng phân bố của biểu đồ cột, nếu biểu đồ có hình dạng bằng phẳng hơn thì sẽ có độ phân tán thấp hơn biểu đổ có hình dạng

nhấp nhô.

Sự chênh lệch giá trị của các cột lớn hơn thì có độ phân tán lớn, ngược

lại chênh lệch giữa các cột nhỏ thì có độ phân tán thấp.

Bài tập 3:

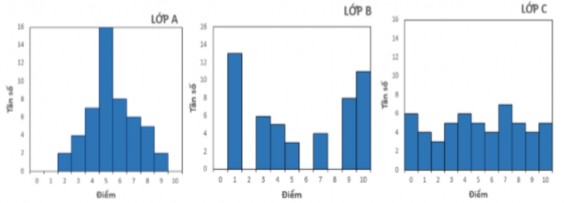
1) Dựa vào đặc điểm của các biểu đồ, hãy cho biết điểm của lớp nào có độ phân tán thấp nhất, cao nhất. Giải thích.

+ Điểm của lớp A có độ phân tán thấp nhất vì biểu đồ có đỉnh trung tâm lớn nên có nhiều giá trị gần với giá trị trung bình nhất.

+ Điểm của lớp B có độ phân tán cao nhất vì biểu đồ có dạng hình chữ U nên có nhiều giá trị cách xa giá trị trung bình nhất.

2) Anh (Chị) hãy đánh giá tính đúng/sai của các câu trả lời trên và giải thích rõ tại sao đúng/sai.

Học sinh

Đúng/Sai	Giải thích
HS1	Sai	Vì các biểu đồ cho là biểu đồ histogram, chiều cao của cột dữ liệu biểu diễn tần số chứ không phải giá trị dữ liệu nên không thể sử dụng chênh lệch chiều cao của các cột để so sánh độ phân tán của dữ liệu.
HS2	Đúng	Vì biểu đồ histogram A có đỉnh trung tâm có tần số lớn nên có nhiều giá trị tập trung xung quanh giá trị trung bình nên sẽ có độ phân tán thấp hơn, biểu đồ C có dạng hình chữ U có nhiều giá trị cách xa giá trị trung bình nên sẽ có độ phân tán lớn nhất.
HS3	Sai	Vì số lượng giá trị dữ liệu không đo độ phân tán của dữ liệu.

Thang đánh giá bài tập 3.2

Mã số

Sự miêu tả
4	Xác định chính xác tính đúng/sai và giải thích rõ ràng cho câu trả lời của cả ba HS.
3	Xác định chính xác tính đúng/sai nhưng chỉ đưa ra lời giải thích đúng cho câu trả lời hai trong ba HS trong đó có câu trả lời đúng của HS2.
2	Xác định chính xác tính đúng/sai nhưng chỉ đưa ra lời giải thích đúng cho câu trả lời của một HS.
1	Xác định tính đúng/sai không chính xác và có đưa ra lời giải thích cho câu trả lời của các HS nhưng không đúng.
0	Không xác định được tính đúng/sai và giải thích sai, không có yếu tố toán học phù hợp trong câu trả lời hoặc không đưa ra bất kì phản hồi nào.

3) Hãy dự đoán xem lí do nào mà mỗi học sinh đã đưa ra câu trả lời như trong câu hỏi 2) ở trên.

Học sinh

Dự đoán lí do đưa ra các câu trả lời của học sinh
HS1	HS nhầm lẫn biểu đồ histogram là biểu đồ cột nên dựa vào sự chênh lệch của các cột để suy ra độ phân tán của dữ liệu.
HS2	HS nắm được khái niệm độ phân tán và biết so sánh độ phân tán dựa vào hình dạng phân bố của biểu đồ cột.
HS3	HS chưa nắm được khái niệm độ phân tán của dữ liệu được biểu diễn trên biểu đồ histogram, cho rằng biểu đồ nào có nhiều cột giá trị dữ liệu nhất thì có độ phân tán cao nhất.

Thang đánh giá bài tập 3.3

Mã số

Sự miêu tả
4	Đưa ra những dự đoán hợp lí, rõ ràng cho câu trả lời của cả 3 HS.
3	Đưa ra dự đoán hợp lí, rõ ràng cho 2 trong 3 câu trả lời của các HS.
2	Đưa ra dự đoán hợp lí, rõ ràng cho 1 trong 3 câu trả lời của các HS.
1	Đưa ra dự đoán cho câu trả lời của các HS nhưng không có ý nghĩa dự đoán.
0	Không đưa ra bất kì phản hồi nào.

Bài tập 3.4

Theo anh (chị), học sinh THPT sẽ gặp những khó khăn hay sai lầm gì khi so sánh độ phân tán của dữ liệu được trình bày dưới dạng biểu đồ histogram như Bài tập 3 này (dự đoán ít nhất ba khó khăn/sai lầm và lí giải).

STT

Khó khăn, sai lầm của HS khi làm bài tập 3.1
1	HS không nắm được khái niệm độ phân tán và không biết được độ phân tán được đánh giá thông qua những tham số nào.
2	HS không xác định được loại biểu đồ histogram và không biết cách đọc thông tin trên biểu đồ.
3	HS mắc sai lầm cho rằng biểu đồ histogram nào có sự chênh lệch các cột nhiều nhất thì có độ phân tán cao nhất hoặc chỉ so sánh trung bình để kết luận.

HS mắc sai lầm cho rằng biểu đồ histogram nào có số lượng cột nhiều hơn thì có độ phân tán lớn hơn.
5	HS chỉ biết so sánh độ phân tán của dữ liệu dựa vào việc tính toán giá trị của các tham số thống kê chứ chưa biết dựa vào hình dáng của biểu đồ histogram để so sánh độ phân tán của dữ liệu.
6	Sai lầm về hình nhận hình dạng biểu đồ: 6A: Biểu đồ càng trải đều thì độ phân tán càng cao 6B: Biểu đồ có cột trung tâm cao nhất thì có độ phân tán cao nhất
7	Không xác định được giá trị trung bình trên biểu đồ histogram