Diện Tích Dưới Đường C Ng Đ C Trưng H Ạt Động Của Bộ Thu Nhận

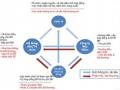
huấn luyện được d ng để ước lượng tham số mô hình. Dữ liệu kiểm tra d ng để kiểm định mô hình đã ước lượng với dữ liệu huấn luyện. Ý tưởng là dành nhiều dữ liệu huấn luyện ước lượng mô hình để có những giá trị tham số ổn định.

áp dụng mô hình vào dữ liệu kiểm tra

Dữ liệu huấn luyện

Ước lượng tham số mô hình

Dữ liệu đầy đủ

Dữ liệu kiểm tra

Hình 3.2: Chiến ược d ng v iể định ô hình

N : N ễ ă ấ 2 2

3.4.6. Kiể định mô hình hồi quy logistic

3.4.6.1. Tiêu chí thông tin Akaike

Tiêu chí thông tin Akaike (Akaike Information Criterion - AIC). Trong mô hình hồi quy logistic, theo Hastie, T. và cộng sự (2016), AIC được định nghĩa là:

( ̂)

Trong đó là số mẫu khảo sát, ( ̂) là giá trị lớn nhất cùa hàm likelihood của mô hình trên tập dữ liệu, log() có cơ số e được gọi là logarit tự nhiên và là số tham số trong mô hình.

Để sử dụng tiêu chí AIC cho việc lựa chọn mô hình, chúng tôi chỉ cần chọn mô hình có AIC nhỏ nhất trong tập hợp các mô hình được xem xét (Hastie, T. và cộng sự, 2016)

3.4.6.2. Tiêu chí thông tin Bayesian

Trong thống kê, tiêu chí thông tin Bayesian (BIC) là một tiêu chí để lựa chọn mô hình; mô hình có BIC thấp nhất được ưa thích. Một phần, nó dựa trên hàm likelihood và nó liên quan chặt chẽ đến tiêu chí AIC. Khi chọn được mô hình phù

hợp, có thể tăng thêm likelihood bằng cách thêm các tham số, nhưng làm như vậy có thể dẫn đến việc tạo ra một phân tích tương ứng quá chặt chẽ hoặc chính xác với một tập hợp dữ liệu cụ thể và do đó có thể không phù hợp với dữ liệu bổ sung hoặc dự đoán các quan sát trong tương lai. Cả BIC và AIC đều cố gắng giải quyết vấn đề này bằng cách đưa ra một điều khoản phạt cho số lượng tham số trong mô hình; mức độ phạt trong BIC lớn hơn trong AIC (Murphy, K. P., 2012).

Schwarz (1978) đã phát triển BIC bằng cách ông ta đã đưa ra một lập luận Bayesian cho việc áp dụng nó và được xuất bản trong một tạp chí khoa học.

BIC được định nghĩa trong hồi quy logistic như sau (Hastie, T. Và cộng sự, 2016):

( ̂) ( )

Trong đó ( ̂) là giá trị lớn nhất cùa hàm likelihood của mô hình trên tập dữ liệu, log() có cơ số e được gọi là logarit tự nhiên, là số số mẫu khảo sát và là số tham số trong mô hình.

3.4.6.3. Ma trận nhầm lẫn

Làm thế nào chúng ta có thể đo lường hiệu quả mô hình của mình hiệu quả tốt hơn, hiệu suất tốt hơn Và đó là lí do ma trận nhầm lẫn (Confusion Matrix) ra đời. Ma trận nhầm lẫn là một phép đo hiệu suất với 4 kết hợp khác nhau của các giá trị dự đoán và thực tế (Stehman và Stephen, 1997) (xem Bảng 3.3).

Bảng 3.3: Ma trận nhầm lẫn

Kết quả

dự báo

Kết quả khảo sát thực tế
Hộ sẵn lòng tham gia	Hộ không sẵn lòng tham gia
Hộ sẵn lòng tham gia	TP	FP
Hộ không sẵn lòng tham gia	FN	TN

Có thể bạn quan tâm!

Xem toàn bộ 251 trang tài liệu này.

Ngu n: Tác gi t ng hợp

1/ TP - True Positive: Dự báo Hộ sẵn lòng tham gia và kết quả thực tế Hộ sẵn lòng tham gia.

2/ FP - False Positive: Dự báo Hộ sẵn lòng tham gia nhưng kết quả thực tế Hộ không sẵn lòng tham gia (Sai số loại 1).

3/ FN - False Negative: Dự báo Hộ không sẵn lòng tham gia nhưng kết quả thực tế Hộ sẵn lòng tham gia.

4/ TN - True Negative: Dự báo là Hộ không sẵn lòng tham gia và kết quả thực tế Hộ không sẵn lòng tham gia (Sai số loại 2).

Ma trận nhầm lẫn cực kỳ hữu ích để đo Độ nhạy, Độ đặc hiệu, Độ chính xác.

+ Độ nhạy (Sensitivity): là tỷ lệ Dự báo hộ sẵn lòng tham gia và kết quả thực tế Sẵn lòng tham gia (TP) trên tổng số hộ sẵn lòng tham gia được khảo sát thực tế ( ).

+ Độ đặc hiệu (Specificity): là tỷ lệ Dự báo là Hộ không sẵn lòng tham gia và kết quả thực tế Hộ không sẵn lòng tham gia (TN) trên tổng số hộ không sẵn lòng tham gia được khảo sát thực tế (TN+FP).

+ Độ chính xác (Accuracy): là tỷ lệ của tổng dự báo đúng (TP+TN) trên tổng số kết quả của khảo sát (TP+FP+TN+FN).

3.4.6.4. Diện tích dưới đường c ng đ c trưng h ạt động của bộ thu nhận

Các thước đo để đánh giá mô hình hồi qui logistic quan trọng nhất gồm độ nhạy, độ đặc hiệu và chỉ số phân định AUC tức là diện tích dưới đường cong đặc trưng hoạt động của bộ thu nhận (Fawcett, Tom 2006). Một mô hình dự báo tốt phải có độ nhạy và độ đặc hiệu cao (gần 1). Tuy nhiên, nếu chúng ta điều chỉnh ngưỡng

xác suất của mô hình dự đoán để tăng độ nhạy thì sẽ làm giảm độ đặc hiệu, hoặc tăng độ đặc hiệu thì sẽ làm giảm độ nhạy. Do đó, biểu đồ đặc trưng hoạt động của bộ thu nhận (ROC) được xem như công cụ dung h a độ nhạy và độ đặc hiệu. Biểu đồ ROC có đồ thị có một tung là Độ nhạy và trục hoành là (1 – Độ đặc hiệu).

ROC là một đường cong xác suất. Đường cong phân phối màu đỏ thuộc nhóm “Hộ sẵn lòng tham gia” (Kết quả khảo sát) và đường cong phân phối màu vàng thuộc nhóm “Hộ không sẵn lòng tham gia” (Kết quả khảo sát).

Trường hợp AUC = 1 (Diện tích hình vuông): Khi hai đường cong hoàn toàn không trùng nhau, mô hình có một số đo lý tưởng về độ phân tách. Nó hoàn toàn có thể phân biệt giữa lớp “Hộ sẵn lòng tham gia” và lớp “Hộ không sẵn lòng tham gia”.

Hình 3.3: Trường hợp AUC = 1

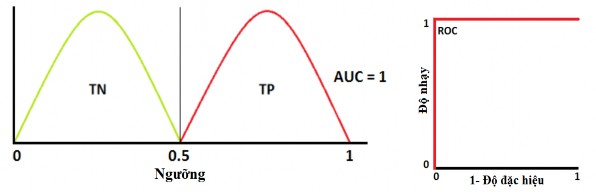
Ngu n: Tác gi t ng hợp

Trường hợp 0.5 < AUC < 1: Khi hai phân phối trùng nhau, sẽ xuất hiện sai số loại 1 và sai số loại 2. Tùy thuộc vào ngưỡng, chúng ta có thể giảm thiểu hoặc tối đa hóa chúng. Khi AUC là 0,7, điều đó có nghĩa là có 70 khả năng mô hình đó sẽ có thể phân biệt giữa lớp tích cực và lớp tiêu cực.

Hình 3.4: Trường hợp 0.5 < AUC < 1

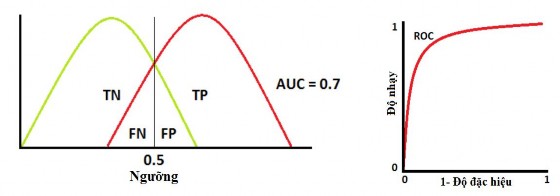
Ngu n: Tác gi t ng hợp

Trường hợp AUC = 0.5 (Diện tích hình tam giác vuông cân): Đây là tình huống tồi tệ nhất. Khi AUC xấp xỉ 0,5, mô hình không có khả năng phân biệt đối xử giữa lớp “Có” và lớp “Không”.

Hình 3.5: Trường hợp AUC = 0.5

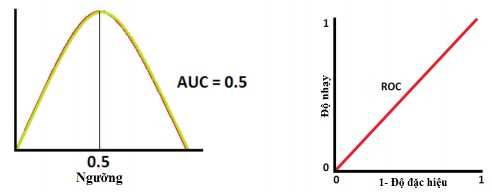
Ngu n: Tác gi t ng hợp

Diện tích AUC tối thiểu là 0,5 và tối đa là 1. Một mô hình dự đoán tốt và có thể áp dụng vào thực tế phải lớn hơn 0,7 (Xem Bảng 3.4). Chỉ số AUC rất có ích trong việc số sánh 2 hay nhiều mô hình khác nhau. Mô hình nào có chỉ số AUC lớn hơn thì mô hình đó có độ chính xác hơn.

Bảng 3.4: Ph n ại chỉ số AUC

AUC

Đánh giá mô hình
≥ 0,9	Rất tốt
0,8 ≤ 0,9	Tốt
0,7 ≤ 0,8	Trung bình
0,6 ≤ 0,7	Không tốt
0,5 ≤ 0,6	Không d ng được

Ngu n: Nguyễ ă ấn (2020)

3.4.6.5. Chỉ số Brier

Điểm Brier được đề xuất bởi Glenn W. Brier vào năm 1950. Nó là một hàm điểm thích hợp để đo độ chính xác của các dự đoán xác suất và nó được áp dụng cho các nhiệm vụ trong đó các dự đoán phải gán xác suất cho một tập hợp các biến rời rạc loại trừ lẫn nhau. Tập hợp các biến có thể có thể là nhị phân hoặc phân loại về bản chất và xác suất được chỉ định cho tập kết quả này phải tổng hợp thành 1. (trong đó m i xác suất riêng lẻ nằm trong khoảng từ 0 đến 1).

Chỉ số Brier được biểu diễn như sau:

∑(

)

trong đólà xác suất được dự đoán,kết quả thực tế của sự kiện tại điểm t (0 nếu điều đó không xảy ra và 1 nếu điều đó xảy ra), N là số trường hợp dự báo.

Trong thực tế, đó là sai số bình phương trung bình của dự báo. Do đó, điểm Brier càng thấp đối với một tập hợp các dự đoán thì càng tốt. Lưu ý rằng điểm Brier có giá trị giữa 0 và 1 vì xác suất dự đoán luôn nằm giữa 0 và 1 nên ta có thể kết luận rằng điểm Brier càng gần 0 thì mô hình càng chính xác.

3.4.6.6. Bootstrap

Phương pháp bootstrap (Efron. B, 1979) dựa vào lý thuyết chọn mẫu ngẫu nhiên có hoàn lại. Phương pháp chọn mẫu này nhằm mục đích tạo ra nhiều mẫu ngẫu nhiên từ một mẫu, và qua cách chọn này, tập hợp những mẫu có thể đại diện cho một quần thể. Một ưu điểm lớn của bootstrap là tính đơn giản của nó. Đây là một cách đơn giản để lấy được các ước tính về sai số tiêu và khoản tin cậy cho các ước lượng phức tạp của phân phối, chẳng hạn như điểm phân vị, tỷ lệ, tỷ lệ chênh lệch và hệ số tương quan. Bootstrap cũng là một cách thích hợp để kiểm soát và kiểm tra tính ổn định của kết quả. Mặc d đối với hầu hết các bài toán, không thể biết khoảng tin cậy thực sự, nhưng về mặt cơ bản thì bootstrap chính xác hơn các khoảng tiêu chuẩn thu được bằng cách sử dụng phương sai mẫu và các giả định về độ chuẩn (DiCiccio TJ, Efron B, 1996). Bootstrap cũng là một phương pháp thuận tiện giúp tránh chi phí lặp lại thử nghiệm để lấy các nhóm dữ liệu mẫu khác. Chính vì thế mà phát triển của phương pháp bootstrap được xem là một cuộc cách mạng quan trọng trong khoa học thống kê ở thế kỷ 21. Phương pháp Bootstrap sẽ được tác giả sử dụng trong việc tính chỉ số AUC của mô hình hộ nông dân sẵn l ng tham gia bảo hiểm cây cà phê theo chỉ số năng suất.

3.4.7. Xây d ng t n đồ

Theo Grimes (2008), Kattan và cộng sự (2010), một toán đồ (nomogram) bao gồm một tập hợp n thang đo, một thang đo tương ứng cho m i biến trong một phương trình. Khi biết các giá trị của (n-1) biến thì giá trị của biến không xác định có thể dự đoán được. Từ biểu đồ sẽ thu được kết quả dự báo rất nhanh và đáng tin cậy bằng vài thao tác với máy tính. Người dùng chỉ cần tra cứu dữ liệu thì có thể thu được kết quả dự báo vấn đề quan tâm. Trong luận án này, tác giả sẽ xây dựng toán đồ của mô hình nghiên cứu việc hộ nông dân sẵn l ng tham gia bảo hiểm cây cà phê theo chỉ số năng suất. Toán đồ với một mô hình sẽ được trình bày trong phần kết quả chương 4.

3.5. Kết luận chư ng 3

Trong chương 3, tác giả trình bày quy trình nghiên cứu, khu vực nghiên cứu. Đồng thời, tác giả liệt kê các phương pháp nghiên cứu định tính gồm phương pháp trao đổi tay đôi, phương pháp hội thảo khoa học, phương pháp chuyên gia để có thêm các bằng chứng đáng tin cậy nhằm củng cố các yếu tố nghiên cứu. Ngoài ra, tác giả trình bày phương pháp nghiên cứu định lượng như thống kê mô tả, sử dụng phương pháp BMA theo hồi quy logistic và phương pháp BMA theo hồi quy probit để xác định mô hình và các biến số liên quan. Bên cạnh đó, tác giả sử dụng sử dụng kỹ thuật tách dữ liệu cũng như các chỉ số AIC, BIC, xác suất hậu định, ma trận nhầm lẫn và AUC để kiểm định và phân tích mô hình. Cuối chương, tác giả trình bày việc xây dựng toán đồ của mô hình nhằm dự đoán nhanh khả năng tham gia bảo hiểm cà phê của hộ nông dân.