Tính Toán, Mô Phỏng Số Hiệu Quả Giảm Dao Động Xoắn Cho Trục Máy

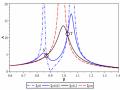
DVA-MQT là thiết kế DVA với các nghiệm tối ưu được xác định theo phương pháp cực tiểu mô men bậc hai, công thức (3.78) và (3.79).

DVA-MEVR là thiết kế DVA với các nghiệm tối ưu được xác định theo phương pháp cực đại độ cản tương đương, công thức (3.87) và (3.88).

và tương tự như vậy DVA-MKE là thiết kế DVA với các nghiệm tối ưu được xác định theo phương pháp cực tiểu hóa năng lượng, công thức (3.96) và (3.97).

Gọi E là phần năng lượng truyền từ trục (hệ chính) sang bộ hấp thụ động lực DVA [2], [15]. Ta có [2]:

E (t)a(t)

(4.1)

Để có thể phân tích và đánh giá hiệu quả giảm dao động của các thiết kế DVA theo từng phương pháp, tiêu chuẩn tính toán và các kích động khác nhau, tác giả sử dụng công thức trong [2], [15]:

k l

ˆ2[i] ˆ2[i]

H 



k

ˆ2[i]



.100%

(4.2)

Trong đó:

H là hiệu quả giảm dao động khi kết cấu có lắp DVA, %

k

ˆ là đường bao đáp ứng của kết cấu khi chưa lắp DVA, rad



l

ˆ là đường bao đáp ứng của kết cấu khi lắp DVA, rad

4.1. Tính toán, mô phỏng số hiệu quả giảm dao động xoắn cho trục máy

Để thực hiện tính toán và mô phỏng số hiệu quả giảm dao động xoắn của trục máy tác giả sử dụng số liệu mô phỏng trong công bố [35] của GS Hosek và các cộng sự (Hình 1.2, chương 1 luận án này). Số liệu mô phỏng như sau:

Trục máy có độ cứng xoắn ks=k1=1.125.105 kgm2/s2

Trục máy chịu cản môi trường có hệ số cản nhớt cs=c1=22.5 kgm2/s

Mô men quán tính khối lượng của trục Jr=I1=1.125.10-1 kgm2

Trục có bán kính quán tính ρr=0.15 m

83

Các số liệu thiết kế đã biết (được chọn trước và yêu cầu kỹ thuật của quy trình thiết kế và lắp ráp) của bộ hấp thụ DVA bao gồm:

- Số lò xo-cản nhớt sử dụng: n = 4

- Bán kính quán tính của đĩa DVA: ρa = 0.15 m

- Khoảng cách lắp ráp lò xo: e1 = 0.075 m

- Khoảng cách lắp bộ cản nhớt: e2 = 0.12 m

- Khối lượng đĩa DVA: ma = 0.2 kg

- Mô men quán tính khối lượng của đĩa DVA: Ja = 4.5.10-3 kgm2

Với bộ số liệu trên, các đại lượng không thứ nguyên được xác định như sau:

- Tỷ số khối lượng: μ = 0.04 = 4%

- Tỷ số bán kính quán tính khối lượng: η = 1

- Tỷ số vị trí lắp lò xo: γ = 0.5

- Tỷ số vị trí lắp cản nhớt: λ = 0.8

Các giá trị tối ưu của tỷ số α và tỷ số cản nhớt  xác định theo các phương pháp trên được thống kê trong bảng 4.2.

Bảng 4.2. Dữ liệu số của các tham số tối ưu

Phương pháp tính toán

αopt	ξopt
Hai điểm cố định	0.961	0.093
Cực tiểu mô men bậc hai	0.971	0.076
Cực đại độ cản tương đương	0.980	0.078
Cực tiểu hóa năng lượng	0.951	0.076

Có thể bạn quan tâm!

• Nghiên Cứu, Phân Tích, Tính Toán Và Xác Định Các Tham Số Tối Ưu Của Bộ Hấp Thụ Dao Động Dva
• Đồ Thị Hàm Khuếch Đại Biên Độ - Tần Số Với Α=0.9, Μ=0.04, Η=1,
• Xác Định Tham Số Tối Ưu Trong Trường Hợp Trục Chịu Kích Động Va Chạm
• Mô Phỏng Số Trường Hợp Trục Máy Chịu Tác Dụng Của Kích Động Va Chạm.
• Năng Lượng E Với Dva-Mevr Khi Hệ Chính Không Cản Chịu Kích Động Ngẫu Nhiên
• Sự Thay Đổi Của Đường Cong Khuếch Đại Biên Độ Khi Thay Đổi Tỷ Số Cản Với

Xem toàn bộ 153 trang tài liệu này.

4.1.1. Mô phỏng số trường hợp hệ chịu tác dụng của kích động điều hòa.

Như phân tích trong chương 3 của luận án này, khi hệ chính chịu kích động điều hòa thì phương pháp xác định tham số tối ưu của bộ hấp thụ động lực DVA phù hợp nhất là phương pháp hai điểm cố định. Điều này có nghĩa là khi hệ chính chịu kích động điều hòa, ta nên sử dụng thiết kế tối ưu DVA-FPM.

Trong phần này, tác giả mô phỏng số với trường hợp trục máy chịu xoắn có lắp bộ hấp thụ DVA-FPM và chịu tác động của mô men kích động điều hòa có dạng:

M=M0sin(ωt) với M0 = 200 Nm.

Để thấy được hiệu quả giảm dao động xoắn của các thiết kế DVA tối ưu khác nhau, khi mô phỏng tác giả thực hiện trên ba trường hợp hệ chính không cản, có cản bé (cs = 5 kgm2/s) và cản lớn (cs = 22.5 kgm2/s [35]).

Điều kiện ban đầu như sau:

2

r (0)  10 rad

1

r(0)  0s

a (0)  0rad

1

a(0)  0s

Các đáp ứng của hệ chính và của bộ hấp thụ dao động khi hệ chính chịu tác động của kích động điều hòa có tần số kích động nằm ngoài vùng cộng hưởng (ω = 62.8 s-1) được thể hiện từ hình 4.1 đến hình 4.3.

Hình 4.1. Dao động xoắn của trục trong giai đoạn chuyển tiếp ban đầu với tần số ω =

62.8 s-1 của kích động

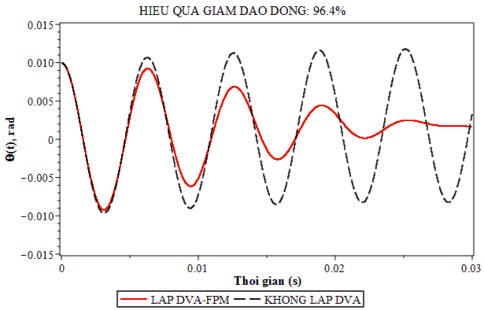
Từ kết quả mô phỏng trên các hình 4.1 ta thấy rằng khi chưa lắp bộ hấp thụ dao động dao động xoắn của trục có dạng tuần hoàn với biên độ không thay đổi (0.02 rad). Nhưng khi lắp bộ hấp thụ dao động DVA-FPM dao động xoắn của trục được giảm rất nhanh trong giai đoạn chuyển tiếp (hình 4.1).

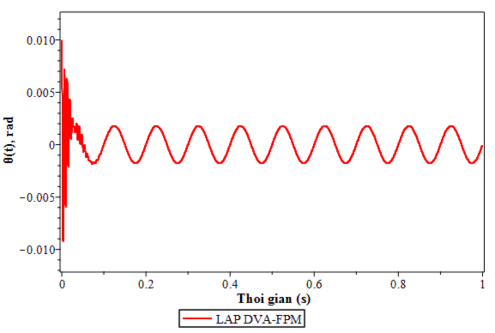
Hình 4.2. Dao động xoắn của trục trong giai đoạn bình ổn với tần số kích động ω = 62.8 s-1 của kích động

Từ kết quả mô phỏng trên các hình 4.2, trong giai đoạn dao động bình ổn (từ 0.1s trở đi), biên độ dao động xoắn chỉ còn 0.004 rad so với 0.02 rad khi chưa lắp DVA. Điều này cho thấy hiệu quả giảm dao động với cả bốn thiết kế DVA được trình bày trong luận án là tốt. Hiệu quả giảm dao động được tính theo công thức (4.2) trong trường hợp này là 96.4%.

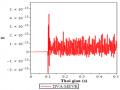
Từ đồ thị trên hình 4.3 mô tả phần năng lượng E cho thấy rằng phần lớn đồ thị nằm ở phía trên trục hoành. Nên khi lấy tổng tích phân của E sẽ là một số dương. Vì vậy năng lượng truyền từ trục sang bộ hấp thụ dao động DVA cũng là dương. Điều này chứng tỏ việc lắp thêm DVA-FPM có tác dụng tốt trong việc giảm năng lượng dao động của hệ chính.

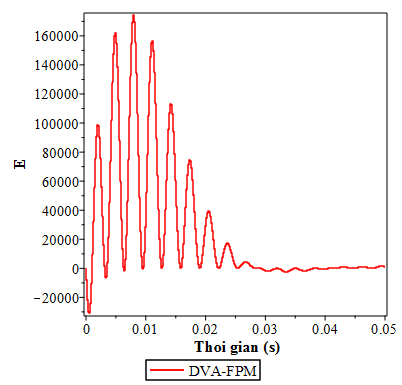
Hình 4.3. Đồ thị mô tả năng lượng E với tần số ω = 62.8 s-1 của kích động

Các mô phỏng và tính toán trên đây được thực hiện với trường hợp kích động có tần số nằm ngoài vùng cộng hưởng của hệ. Trường hợp tần số của kích động bằng tần số riêng của hệ, hệ sẽ xảy ra cộng hưởng với biên độ lớn và rất nguy hiểm.

Tần số riêng của cơ hệ được xác định như sau:

det(M2 K) 0 (4.3)

ks

Jr Ja

Trong trạng thái cản tới hạn ∞, bộ hấp thụ DVA và trục máy coi như bó cứng thành một vật có mô men quán tính khối lượng là Jr+Ja, khi đó tần số cộng hưởng được xác định như sau:



re (4.4)

Thay các số liệu mô phỏng ở trên và các phương trình (2.33), (2.35) vào phương trình (4.3) và giải phương trình này thu được hai tần số cộng hưởng của cơ hệ là ωre1 và ωre3. Từ phương trình (4.4) ta thu được tần số cộng hưởng ωre2.

Các tần số cộng hưởng của cơ hệ theo các thiết kế tối ưu DVA khác nhau được liệt kê trong bảng 4.3.

Bảng 4.3. Tần số cộng hưởng của hệ

Tần số cộng hưởng

ωre1	ωre2	ωre3
DVA-FPM	887.41	980.58	1083.52

Trong các tính toán và mô phỏng số sau đây tác giả thực hiện với tần số của kích động là ω = 1000 s-1 (hệ làm việc trong vùng cộng hưởng) [35]. Các đáp ứng của hệ chính khi lắp bộ hấp thụ dao động DVA-FPM khi hệ làm việc trong vùng cộng hưởng được thể hiện trên các hình 4.4 đến hình 4.6.

a) Hệ chính không cản (cs = 0)

b) Hệ chính có cản nhỏ (cs = 5kgm2/s)

c) Hệ chính có cản (cs = 22.5 kgm2/s)

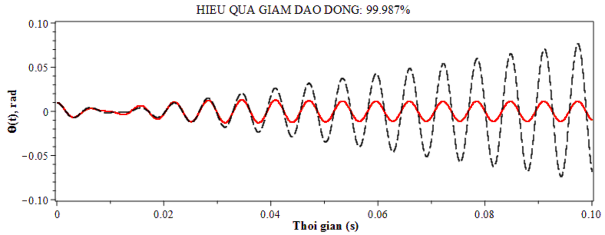
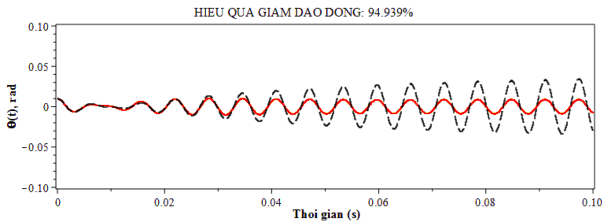
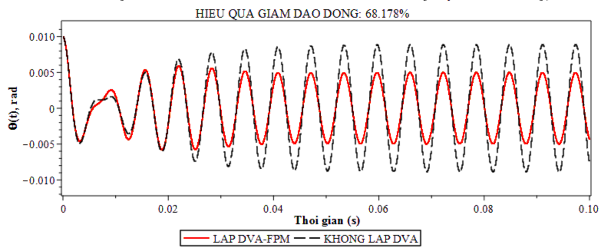
Hình 4.4. Đáp ứng của hệ khi lắp và không lắp DVA-FPM

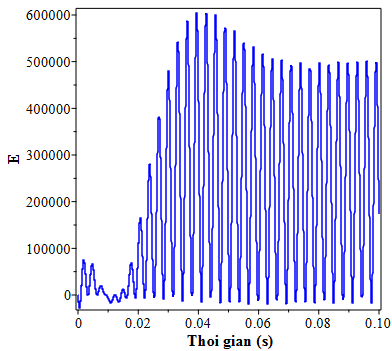
Hình 4.5. Đồ thị mô tả năng lượng E với DVA-FPM, hệ chính không cản.

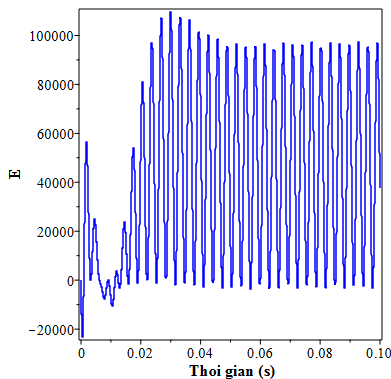
Hình 4.6. Đồ thị mô tả năng lượng E với DVA-FPM, hệ chính có cản, cs=22.5 kgm2/s Bảng 4.4. Hiệu quả giảm dao động của các thiết kế DVA khi hệ chính chịu kích động tuần hoàn với tần số cộng hưởng.

Thiết kế DVA

Hiệu quả giảm dao động (%)
cs = 0 kgm2/s	cs = 5 kgm2/s	cs = 22.5 kgm2/s
DVA-FPM	99.987	94.939	68.178

Hình 4.4 đến hình 4.6 mô tả hiệu quả giảm dao động xoắn của trục máy khi lắp bộ hấp thụ dao động DVA-FPM. Khi hệ chịu kích động tuần hoàn với tần số của kích động là ω = 1000s-1 (vùng tần số cộng hưởng), kết quả tính toán hiệu quả giảm dao động xoắn theo công thức (4.2) được liệt kê trong bảng 4.4.

Từ các hình 4.4 đến 4.6 và bảng 4.4 ta thấy rằng ngay cả trong trường hợp hệ chịu kích động tuần hoàn và làm việc trong vùng cộng hưởng, hiệu quả giảm dao động xoắn khi lắp DVA-FPM vẫn rất tốt. Trong khi với trường hợp khi chưa lắp DVA-FPM biên độ dao động xoắn của trục có xu hướng tăng thì khi lắp DVA-FPM với thiết kế tối ưu biên độ dao động xoắn được giữ bình ổn với giá trị nhỏ so với khi chưa lắp. Cụ thể với việc lắp bộ hấp thụ DVA-FPM (hình 4.4), sau khoảng 0.04s đầu tiên dao động xoắn

Xem tất cả 153 trang.