1
C n244 (1 2 )2
2 4 2 2 2 2 2 4
C2 n(1) n(2 )
C 4242m2n3
3 r r s
2 4 2 2 2 2 2 4
C4 n n(1 ) (2 )
Giải hệ phương trình (3.76), (3.77) ta thu được các tham số tối ưu của bộ hấp thụ động lực DVA:
2
n(2 2 )
opt 2
2 2(4 32 )
22 n(12 )(2 2 )
n(12 )
(3.78)
opt
Xác định tham số tối ưu theo phương pháp cực đại độ cản tương đương.
Từ hệ phương trình vi phân dao động (2.37), (2.38) ta biến đổi về dạng:
(3.79)
m 2k nk e2nc e2
M (t)
(3.80)
r r s a 1 a a 2 a
Từ (3.80) ta xác định được mô men cản tương đương tác dụng lên trục máy (hệ chính) như sau:
M nk e2
nc e2(3.81)
eqv a 1 a a 2 a
Thay các đại lượng không thứ nguyên trong các phương trình (3.20)-(3.23) vào phương trình (3.81), ta có:
M nm 2222nm 22(3.82)
eqv a s r a a s r a
M
2
n
m
2 2
a s r a
nm
2
2 2 2
a
s r a
2
Hệ số cản tương đương của bộ hấp thụ động lực DVA tác động vào hệ chính được xác định như sau:
ctd
(3.83)
Xét trường hợp hệ chính chịu tác dụng của kích động ngẫu nhiên ồn trắng, các giá trị trung bình trong (3.83) là các thành phần của ma trận mô men bậc hai trong phương trình ma trận Lyapunov (3.62) [39], nghĩa là:
nm 2 2P nm 222 2P
ctd
a s r 34 a s r 32
P33
(3.84)
Để cực đại ctđ điều kiện cực đại của hàm hai biến được áp dụng vào phương trình (3.84). Ta có:
ctd
0
*
c td
0
*
(3.85)
(3.86)
Giải hệ phương trình (3.85), (3.86) ta thu được các tham số tối ưu của bộ hấp thụ động lực DVA như sau:
opt
*
n(12)
2
2
n
*
(3.87)
opt
3.3. Xác định tham số tối ưu trong trường hợp trục chịu kích động va chạm
(3.88)
Trong phần này trình bày tính toán xác định tham số tối ưu cho DVA bằng cách sử dụng phương pháp cực tiểu hóa năng lượng với hàm mục tiêu là tích phân năng lượng gây ra dao động cho hệ chính đạt cực tiểu. Mục đích chính là giảm thành phần dao động riêng của hệ chính.
Ta dùng phép đổi biến số như sau:
y1
y2 a
y3y1
(3.89a)
y4y2a
Từ phương trình vi phân dao động (3.5) đưa về phương trình:
y
trong đó:
By + F
y1
(3.89b)
y
y
2 a
y
3
y4 a
F là véc tơ lực kích động trong (3.12)
M (t)
F m 2
r r
0
Ma trận B được xác định trong (3.61)
0 0 1 0
0 0 0 1
B 2
n222
0 n
2
s s s
2
12 n222
12 n222
s
0
s 2 2
s
Mục tiêu của luận án ở phần này là thiết kế tối ưu bộ hấp thụ động lực DVA nhằm giảm thành phần dao động riêng của cơ hệ nên ta xét phương trình vi phân dao động tự do của cơ hệ ứng với phương trình (3.89b) như sau :
y By
(3.89c)
với điều kiện đầu là y(0) = y0
Trong phần này tác giả sử dụng phương pháp cực tiểu hóa năng lượng sử dụng phiếm hàm động năng theo các tài liệu [63], [64]. Bài toán đặt ra là thiết kế các thông số của bộ hấp thụ động lực DVA sao cho phiếm hàm năng lượng
L 1 yT Pyo
(3.90)
2o
đạt giá trị cực tiểu, trong đó y0 là véc tơ điều kiện ban đầu, ma trận P là nghiệm của phương trình đại số Lyapunov
BT P PB Q (3.91a)
Với Q là ma trận trọng số. Với mục tiêu là cực tiểu năng lượng của hệ chính sử dụng phiếm hàm động năng nên ma trận trọng số Q sẽ được chọn như sau:
0 0 0 0
0 0 0 0
Q
(3.91b)
0 0 Q33 0
0 0 0 0
trong đó Q33 là trọng số.
Trong trường hợp này nó chỉ có tác dụng như một hằng số nhân và không ảnh hưởng đến kết quả tính toán tối ưu, do đó để đơn giản ta chọn Q33 = 1, như vậy ma trận trọng số Q sẽ có dạng:
0 0 0 0
0 0 0 0
Q
0 0 1 0
0 0 0 0
(3.92)
Thay các ma trận trong (3.61) và (3.92) vào phương trình Lyapunov (3.91) và giải hệ phương trình này ta thu được ma trận P như sau:
P11 P12 P13 P14
P P P P
P
21 22 23 24
P31 P32 P33 P34
(3.93)
P P P P
trong đó:
41 42 43 44
P11
D1D2D3s
D4
1
D n244 (12 )2
2
D n24 (12 )
D 4 n222 (2 2 ); D 2n24
P22
P33
3 4
s
34n
22
E1 E2
E3
1
E 4n244 (12)3
2 2 2 4 2 2 2
E2n1n1 2
3
s
E 2n24
P44
n 24 (12 ) 42
2
P12 P21
s
s
2n22(12) 2
222
P P 1
13 31 2
P P 1
14 41
P23 P32
2
n22 (1 2 ) 22
P P
1 n22 ;
P P
G1 G2
24 42 2
34 43
3
G
1
G n3442n(24 42 )
G 2 n(224 42 ) 2 G 222
2 3 s
Thay (3.93) vào (3.90) ta tìm được phiếm hàm L như sau:
n244(12)3
L / 4n24
0 2 2 2 2 4 2 2 2 2 4
(1) n (1) 2n
s (3.94)
Để cực tiểu hàm mục tiêu L, điều kiện cực tiểu của hàm hai biến được áp dụng:
L
L
0
*
(3.95)
0
*
Giải hệ phương trình (3.94, 3.95) ta tìm tham số tối ưu cho DVA là:
2n(2 2 )
*
2n(1 2 )
2 (4 32 24 )
(12 )2 2n(2 2 )
*
(3.96)
(3.97)
3.4. Các bước thiết kế bộ hấp thụ dao động DVA giảm dao động xoắn cho trục.
Quá trình thiết kế tìm thông số tối ưu của bộ hấp thụ DVA thường được thực hiện theo các bước sau:
Bước đầu tiên: chọn khối lượng và bán kính của bộ hấp thụ dao động theo tỷ lệ ma=μmr và ρa= ηρr để tăng đặc tính tắt dần cho dao động xoắn của trục và sao cho μ chỉ khoảng vài phần trăm để không thay đổi bản chất động lực của cơ hệ [20].
Bước thứ hai chọn số bộ lò xo-cản nhớt n với lưu ý nên chọn n là số chẵn, chẳng hạn, n=2, n=4, … [26].
Bước thứ ba ta chọn vị trí lắp đặt lò xo và bộ cản nhớt của bộ hấp thụ dao động sao cho thuận lợi trong quá trình lắp đặt và chế tạo bộ hấp thụ.
Các thông số ở trên nên được chọn sao cho tỷ số α được tính theo các công thức (3.47), (3.78), (3.87) và (3.96) xấp xỉ bằng 1 và dao động của hệ chính và DVA ngược pha nhau (nghĩa là tần số dao động riêng của bộ hấp thụ DVA và của hệ chính xấp xỉ bằng nhau), khi ấy hiệu quả giảm dao động xoắn cho trục sẽ tốt hơn.
Bước cuối cùng: hệ số lò xo ka và hệ số cản nhớt ca tính toán theo các công thức (3.54) và (3.55) hoặc (3.78), (3.79), (3.87), (3.88), (3.96) và (3.97). Từ đó cho phép ta chọn lò xo và cản nhớt tối ưu cho thiết kế bộ hấp thụ dao động.
3.5. Kết luận chương 3
Chương 3 đã nghiên cứu lý thuyết, tính toán các tham số tối ưu của bộ hấp thụ dao động DVA. Các kết quả nghiên cứu thu được như sau:
Trường hợp 1. Trục máy chịu kích động điều hòa. Các tham số tối ưu được xác định theo phương pháp hai điểm cố định.
![]()
opt
2
2
3
2n(12)
opt
n 2 1
Trường hợp 2. Trục máy chịu kích động ngẫu nhiên
Xác định theo phương pháp cực tiểu mô men bậc hai
2
n(2 2 )
2 2(4 32 ) 22 n(12 )(2 2 )
opt 2
n(12 )
opt
Xác định theo phương pháp cực đại độ cản tương đương
opt
n(12)
2
2
n
opt
Trường hợp 4. Trục máy chịu kích động va chạm. Các tham số tối ưu được xác định theo phương pháp cực tiểu hóa năng lượng.
*
*
2n(2 2 )
2 (4 3224)
(12 )2 2n(2 2 )
2n(12 )
Các kết quả nghiên cứu này được tác giả tính toán và lập trình trên phần mềm Maple, đây là phần mềm được các nhà khoa học trên thế giới chuyên dùng và cho kết quả tin cậy. Để đánh giá và mô phỏng hiệu quả giảm dao động của trục máy khi lắp bộ DVA với các thông số tối ưu tìm được ở trên, tác giả sẽ trình bầy trong chương 4 của luận án.
CHƯƠNG 4. TÍNH TOÁN, MÔ PHỎNG SỐ HIỆU QUẢ GIẢM DAO ĐỘNG VÀ PHÁT TRIỂN CHO HỆ CHÍNH NHIỀU BẬC TỰ DO
Trong chương 3, tác giả đã tính toán và xác định các tham số tối ưu của bộ hấp thụ dao động DVA giảm dao động xoắn cho trục máy. Các kết quả được trình bày dưới dạng nghiệm giải tích tường minh. Từ các kết quả thu được ở chương 3, ta thấy rằng có nhiều tiêu chuẩn thiết kế tối ưu để tìm ra bộ thông số tối ưu cho thiết kế bộ hấp thụ dao động tùy thuộc vào mỗi loại kích động khác nhau tác dụng vào hệ chính. Mỗi tiêu chuẩn tính toán cho ta một kết quả khác nhau. Để thấy được hiệu quả giảm dao động xoắn của việc lắp bộ hấp thụ động lực DVA, trong mục này sẽ trình bày các kết quả tính toán và mô phỏng số với mô hình trục máy có cản và không cản có lắp bộ hấp thụ DVA với các thiết kế theo các nghiệm giải tích đã xác định trong chương 3. Các kết quả giải tích tối ưu được xác định trong chương 3 được liệt kê trong bảng 4.1.
Bảng 4.1. Các tham số tối ưu của bộ hấp thụ dao động theo các phương pháp khác nhau
αopt | ξopt | |
Kích động điều hòa (Hai điểm cố định) | n 2 1 | 2 3 2 2n(12 ) |
Kích động ngẫu nhiên (Cực tiểu mô men bậc hai) | 2 n(2 2 ) 2 n(12 ) | 2 2(4 32 ) 22n(12)(2 2) |
Kích động ngẫu nhiên (Cực đại độ cản tương đương) | n(12 ) | 2 2 n |
Kích động va chạm (Cực tiểu hóa năng lượng) | 2n(2 2) 2n(12) | 2 (4 3224) (1 2)22n(2 2) |
Có thể bạn quan tâm!
-
 Mô Phỏng Số Dao Động Xoắn Của Trục Máy Có Lắp Bộ Hấp Thụ Dva.
Mô Phỏng Số Dao Động Xoắn Của Trục Máy Có Lắp Bộ Hấp Thụ Dva. -
 Nghiên Cứu, Phân Tích, Tính Toán Và Xác Định Các Tham Số Tối Ưu Của Bộ Hấp Thụ Dao Động Dva
Nghiên Cứu, Phân Tích, Tính Toán Và Xác Định Các Tham Số Tối Ưu Của Bộ Hấp Thụ Dao Động Dva -
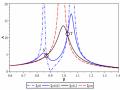
 Đồ Thị Hàm Khuếch Đại Biên Độ - Tần Số Với Α=0.9, Μ=0.04, Η=1,
Đồ Thị Hàm Khuếch Đại Biên Độ - Tần Số Với Α=0.9, Μ=0.04, Η=1, -
 Tính Toán, Mô Phỏng Số Hiệu Quả Giảm Dao Động Xoắn Cho Trục Máy
Tính Toán, Mô Phỏng Số Hiệu Quả Giảm Dao Động Xoắn Cho Trục Máy -
 Mô Phỏng Số Trường Hợp Trục Máy Chịu Tác Dụng Của Kích Động Va Chạm.
Mô Phỏng Số Trường Hợp Trục Máy Chịu Tác Dụng Của Kích Động Va Chạm. -
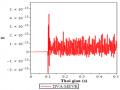
 Năng Lượng E Với Dva-Mevr Khi Hệ Chính Không Cản Chịu Kích Động Ngẫu Nhiên
Năng Lượng E Với Dva-Mevr Khi Hệ Chính Không Cản Chịu Kích Động Ngẫu Nhiên
Xem toàn bộ 153 trang tài liệu này.

Để thuận tiện trong việc tính toán và mô phỏng số và tính toán hiệu quả giảm dao động theo các phương pháp giải tích, tác giả ký hiệu:
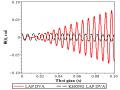
DVA-FPM là thiết kế DVA với các nghiệm tối ưu được xác định theo phương pháp hai điểm cố định theo các công thức (3.47) và (3.55).