Năng Lượng E Với Dva-Mevr Khi Hệ Chính Không Cản Chịu Kích Động Ngẫu Nhiên

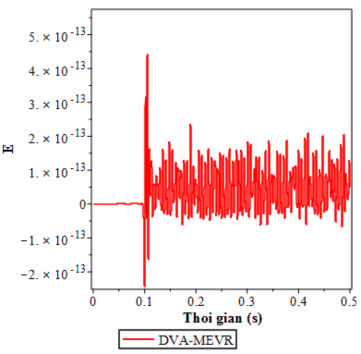
Hình 4.16. Năng lượng E với DVA-MEVR khi hệ chính không cản chịu kích động ngẫu nhiên

Bảng 4.6. Hiệu quả giảm dao động của các thiết kế DVA khi hệ chính chịu kích động ngẫu nhiên

Thiết kế DVA

Hiệu quả giảm dao động (%)
cs = 0 kgms-2	cs = 5 kgms-2	cs = 22.5 kgms-2
DVA-MQT	97.058	95.464	95.758
DVA-MEVR	96.988	95.909	96.013

Có thể bạn quan tâm!

Xem toàn bộ 153 trang tài liệu này.

Từ các kết quả mô phỏng trên các hình 4.11 đến 4.16 và các kết quả tính toán hiệu quả giảm dao động xoắn được liệt kê trong bảng 4.6 ta thấy rằng với cả hai thiết kế tối ưu trong trường hợp hệ chịu kích động ngẫu nhiên đều mang lại hiệu quả giảm dao động tốt (đều đạt trên 95%).

Đặc biệt ta nhận thấy rằng trường hợp hệ chính không cản và có cản hiệu quả giảm dao động chênh nhau không đáng kể (khoảng 1.3% với DVA-MQT và 0.975% với DVA-MEVR). Điều này chứng tỏ nghiệm giải tích tối ưu đã xác định được ở chương 3 không những cho đáp ứng tốt với trường hợp hệ chính không cản mà còn đáp ứng tốt với trường hợp hệ chính có cản.

4.2. Phát triển kết quả nghiên cứu cho trường hợp hệ chính nhiều bậc tự do

4.2.1. Mô hình nghiên cứu và phương trình vi phân dao động xoắn của trục máy nhiều bậc tự do

JrN

Jr ( N 1)

Jr1

Jr 2

0

ksN

ks ( N 1)

ks 2

ks1

Hình 4.17. Mô hình trục máy nhiều bậc tự do lắp bộ hấp thụ dao động DVA Khảo sát mô hình trục máy (hệ chính) có N bậc tự do, mỗi bậc tự do được mô

hình hóa gồm một lò xo xoắn có độ cứng xoắn là ksi và một đĩa có mô men quán tính khối lượng Jri như hình 4.17.

Để giảm dao động xoắn cho trục máy, ta lắp bộ hấp thụ dao động DVA dạng đĩa- lò xo-cản nhớt vào phần ngõng trục thông qua moay ơ (hub) của bộ hấp thụ dao động DVA. Liên kết giữa trục máy và bộ hấp thụ DVA là liên kết then hoa, do đó rotor của DVA sẽ quay cùng trục khi trục máy chuyển động quay. Sơ đồ cấu tạo của bộ hấp thụ dao động DVA được biểu diễn trên hình 2.2 (chương 2 của luận án này).

Cơ hệ khảo sát có N+1 bậc tự do, trong đó hệ chính có N bậc tự do và bộ hấp thụ dao động DVA có một bậc tự do. Chọn tọa độ suy rộng độc lập là góc quay φi của bậc tự do thứ i (i=1, 2, …, N) và góc quay tương đối φa của đĩa DVA so với bậc tự do thứ nhất.

Động năng của cơ hệ

T TaTi

i1

(4.5)

trong đó

T: động năng của cơ hệ;

Ta: động năng của bộ hấp thụ dao động DVA

Ti: động năng của bậc tự do thứ i;

N: số bậc tự do của hệ chính

Động năng của bậc tự do thứ i được xác định như sau:

T 1 J  2

(4.6)

i 2 ri i

Động năng của DVA là:

T 1 J

a 2 a

1

a

(4.7)

Vậy động năng của cơ hệ là:

T 1J  2 1J

2

(4.8)

i1 2

ri i

2 a 1 a

Hàm thế năng của cơ hệ

1

2 N 12

nk (e )

2 a 1 a

ksi (i i1)

i1

(4.9)

trong đó: N 1 0t

Hàm hao tán:

(rad)

1 nc

(e2a)

(4.10)

Phương trình vi phân chuyển động của cơ hệ

Áp dụng phương trình Lagrange loại II cho hệ có N+1 bậc tự do ta có:

d T T

Q* (i  1..N 1)

dt  

 i

(4.11)

i 

trong đó:

i i i

Q* M (t)

i  1

(i  1..N 1)



i i  1

(4.12)

Thay (4.8), (4.9), (4.10) và (4.12) vào phương trình (4.11) ta thu được phương trình vi phân mô tả dao động xoắn của hệ N+1 bậc tự do:

J () nc e2nk e2

a 1 a a 2 a a 1 a

Jr11Ja(1a)ks1 21M (t)

Jr22ks1 21ks2 32

............................................

Jrjj ks( j 1) j j 1 ksj j1 j 

(4.13)

............................................

Jr ( N 1)N 1 ks( N 2) N 1 N 2 ks( N 1) N N 1 

JrNN

ks( N 1) N N 1 ksN N 0t

Gọi θj là góc xoắn của bậc tự do thứ j so với đầu trái của trục, ta có:

j j 0t

( j  1..N )

(4.14)

Gọi θj(j-1) là góc xoắn tương đối của hai bậc tự do liền kề nhau, ta có:

j ( j 1) j j 1 ( j  1..N )

(4.15)

N N 0 N

0 N

0t

(4.16)

Thay (4.14) vào (4.15), ta có:

j ( j 1) j 0t j 1 0t j j 1 ( j  1..N )

(4.17)

Đạo hàm cấp hai theo thời gian hai vế của phương trình (4.14) với lưu ý Ω0=const, ta có:

 

(i  1..N )

(4.18)

j j

Thay (4.15), (4.17) và (4.18) vào hệ phương trình (4.13) ta thu được hệ phương trình vi phân dao động mô tả dao động xoắn của hệ khảo sát như sau:

J () nc e2nk e2

a 1 a a 2 a a 1 a

J  J (  ) k 

M (t)

r1 1 a 1 a s1 2 1

J 

k



k



r 2 2

s1 2 1

s 2 3 2

............................................

Jrj

ks ( j 1) j j 1 ksj j 1 j 

(4.19)

............................................

Jr ( N  k

k



1) N 1

J  k

s ( N 2)



N 1 N 2

k 

s ( N 1)

N N 1

rN N s( N 1)

N N 1

sN N

4.2.2. Nghiên cứu xác định tham số tối ưu của bộ hấp thụ dao động giảm dao động xoắn cho trục máy nhiều bậc tự do

Khi thực hiện tính toán và mô phỏng số các kết quả nghiên cứu trong mục này, tác giả nhận thấy rằng với mô hình trục máy có N bậc tự do, với bậc tự do thứ N các đường cong của hàm khuếch đại biên độ (ứng với mọi giá trị của tỉ số cản nhớt) luôn đi qua các điểm cố định (tồn tại các điểm cố định mà tại các điểm này hàm khuếch đại biên độ của bậc tự do thứ N không phụ thuộc vào tỷ số cản nhớt). Trong khi các bậc tự do khác của mô hình trục máy N bậc tự do không tồn tại các điểm cố định trên đồ thị hàm khuếch đại biên độ của chúng.

Trong phạm vi nghiên cứu của luận án, với mục đích phát triển phương pháp điểm cố định (trình bày trong chương 3 của luận án này với mô hình trục máy một bậc tự do) cho mô hình trục máy N bậc tự do để xác định các tham số tối ưu của bộ hấp thụ dao động DVA, tác giả tập trung thiết lập hàm khuếch đại biên độ và phát triển phương pháp điểm cố định để xác định tham số tối ưu của bộ DVA giảm dao động xoắn cho bậc tự do thứ N. Kết quả mô phỏng số (được trình bày trong mục 4.2.3 của chương này) cho thấy với các tham số tối ưu của bộ hấp thụ dao động DVA không những mang lại hiệu

quả tốt trong việc giảm dao động xoắn cho bậc tự do thứ N và còn có hiệu quả tốt cho các bậc tự do còn lại.

Xác định hàm khuếch đại biên độ A của bậc tự do thứ N

Từ hệ phương trình vi phân dao động xoắn (4.19) ta có tần số dao động riêng của bộ hấp thụ dao động DVA là:

2 k / m

(4.20)

a a a

Ta đặt:

2 k / J

(4.21)

si si ri

Trong phạm vi nghiên cứu phát triển của luận án, tác giả giả định độ cứng xoắn và mô men quán tính khối lượng của mỗi bậc tự do là như nhau:

ks1 ks 2

 ...ksN

ks

(4.22)

J J  ...J J J m 2

(4.23)

r1 r 2 r 3 rN r r r

Do đó ta có: Ωsi = Ωsj = Ωs với i≠j

Ta đặt các đại lượng không thứ nguyên như sau:

μ = ma /mr, η = ρa / ρr, λ = e1 / ρr, α = ωa /Ωs, β = ω /Ωs, ξ = ca /(ma ωa)

Xét trường hợp mô hình trục máy chịu tác động của mô men kích động tuần hoàn (hình 4.17) được biểu diễn dưới dạng phức như sau:

M (t ) Mˆe It

(4.24)

Trong đó:

Mˆlà biên độ phức của kích động

là tần số của lực kích động tuần hoàn

Khi hệ chính chịu tác động của kích động điều hòa thì đáp ứng biên độ của các tọa độ suy rộng được biểu diễn như sau:

i i

ˆeIt

(4.25)

It

aˆae

(4.26)

Trong đó:

i

và ˆa

là biên độ dao động phức của bậc tự do thứ i và DVA

Để xác định được biên độ phức tổng quát cho bậc tự do thứ N, tác giả lần lượt khảo sát mô hình trục máy có N = 1, 2, 3 … bậc tự do.

Xét mô hình trục máy có 1 bậc tự do (N=1)

Đáp ứng biên độ của các tọa độ suy rộng được biểu diễn như sau:

ˆeIt

(4.27)

It

aˆae

(4.28)

Thay N=1 và các phương trình (4.24), (4.27) và (4.28) vào hệ phương trình (4.19) ta thu được hệ phương trình vi phân dao động:

2 2

2 It

2 2 2

It

2 It

Mˆ 2

It 

 (



 1)

se

s ˆ 

se

sˆase

s ˆ 



se s 



22n2eIstˆ

I2n2eIstˆ222eIstˆ222eIstˆ

s a

s a s

s a 

(4.29)

Hệ phương trình (4.29) thu được trùng với hệ phương trình (3.16) cho mô hình SDOF (trình bày trong chương 3 của luận án này). Điều này chứng tỏ độ tin cậy của hệ phương trình vi phân dao động (4.19) khi áp dụng cho mô hình trục 1 bậc tự do. Việc xác định các tham số tối ưu được thực hiện như mục 3.1 của luận án này.

Xét mô hình trục máy có 2 bậc tự do (N=2)

Đáp ứng biên độ của các tọa độ suy rộng được biểu diễn như sau:

ˆ eIt

(4.30)

1 1

2 2

ˆ eIt

(4.31)

It

aˆae

(4.32)

Thay N=2, các đại lượng không thứ nguyên ở trên và các phương trình (4.24), (4.30), (4.31) và (4.32) vào hệ phương trình (4.19) ta thu được hệ phương trình vi phân dao động:

 (2 1)  eI st 222

2 (

) MeI st

2

s a s 1 2

2 s (1  22 )

2(22eIst) eIstn2

(I 22 )

(4.33)

1 a s s a

Giải hệ phương trình (4.33) ta thu được biên độ phức của dao động xoắn của bậc tự do thứ N = 2 (bậc tự do thứ hai) là:

ˆ  (22n 22 ) I(n2 ) M 

X2 IY2



s 

(4.34)

trong đó:



X x

(22n 22 ) y

22n22 222n 



(4.35)

2 2 22 42 22n 



2 2 2

Y x (n2) y 322n 32n 2n(4.36)

x2  1

y2  2 

(4.37)

(4.38)

So sánh các công thức (4.34), (4.35), (4.36) với các công thức (3.20), (3.21), (3.22) và (3.23) ta thu được biên độ phức của dao động xoắn của bậc tự do thứ 2 như sau:

ˆ 

A1 IA2

M 

2 x A y A Ix A y A k 

(4.39)

2 1 2 3 2 2 2 4 s 