Đồ Thị Hàm Khuếch Đại Biên Độ - Tần Số Với Α=0.9, Μ=0.04, Η=1,

Mˆ

ks

1 2

A2 A22

A2 A22

3

4

ˆ 

Có thể bạn quan tâm!

• Tính Toán Tham Số Tối Ưu Trong Trường Hợp Hệ Chính Có Nhiều Bậc Tự Do
• Mô Phỏng Số Dao Động Xoắn Của Trục Máy Có Lắp Bộ Hấp Thụ Dva.
• Nghiên Cứu, Phân Tích, Tính Toán Và Xác Định Các Tham Số Tối Ưu Của Bộ Hấp Thụ Dao Động Dva
• Xác Định Tham Số Tối Ưu Trong Trường Hợp Trục Chịu Kích Động Va Chạm
• Tính Toán, Mô Phỏng Số Hiệu Quả Giảm Dao Động Xoắn Cho Trục Máy
• Mô Phỏng Số Trường Hợp Trục Máy Chịu Tác Dụng Của Kích Động Va Chạm.

Xem toàn bộ 153 trang tài liệu này.

(3.26)

Đặt:

A A 

2

2 2

1 2

A A 

2

2 2

3

4

A (3.27)

A được gọi là hàm khuếch đại biên độ.

X 2 Y 2

V 2 W 2

Thay các hệ số A1, A2, A3, A4 trong các phương trình (3.20)-(3.23) vào biểu thức (3.27) trên ta thu được hàm khuếch biên độ-tần số đại như sau:

A (3.28)

Trong đó:

X n2

Y 22 n22

V 3n22 32n2n

W 2322n 222n 

22 42 22n

(3.29)

(3.30)

(3.31)

(3.32)

Hàm khuếch đại A với  0

A 0

(3.33)

H

K

trong đó

H 22n 22

K 2 222 n 2 22n 42 22n 22

Hàm khuếch đại A với 

1

442 242 2224 221

A 

(3.34)

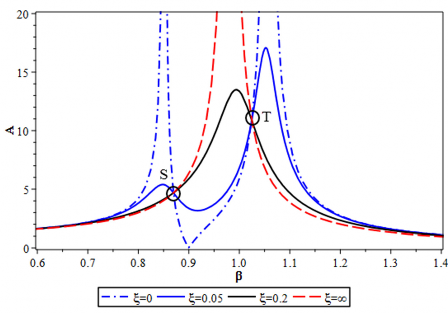
Hình 3.1. Đồ thị hàm khuếch đại biên độ - tần số với α=0.9, μ=0.04, η=1,

γ=0.5, λ=0.8 và n=4.

Hình 3.1 mô tả đồ thị của hàm khuếch đại biên độ-tần số A theo tỷ số cản nhớt ξ.

Ta thấy rằng với hai trường hợp tới hạn

 0 (không cản) và (cản tới hạn) đều

dẫn tới đỉnh của đồ thị hàm khuếch đại tiến ra vô cùng. Điều đó cho thấy giữa hai giá trị này tồn tại một giá trị tối ưu nào đó của tỉ số cản . Ngoài ra tính chất không cản của hệ chính dẫn tới sự tồn tại của hai điểm cố định S, T không phụ thuộc vào tỉ số cản của bộ hấp thụ dao động DVA.

Bước đầu tiên của phương pháp điểm cố định là tìm hai điểm cố định S, T. Giả sử hai điểm S, T có hoành độ là β1, β2.

Để A không phụ thuộc vào ξ thì:

A 0



(3.35)

Thay (3.27) vào (3.35) ta có:



( A2 A2 A2 A2 )

A A 

2

2 2

1 2

A A 

2 2 2

3 4

1 4 2 30

(3.36)

2 2 2 2

A4A3 

Từ (3.36) ta có:

1 4 2 3

A2 A2 A2 A2  0

1 4 2 3

A2 A2 A2 A2

(3.37)

(3.38)

A2 A2

12

(3.39)

A2 A2

3 4

từ đó suy ra:

A1

A3

A2

A4

(3.40)

22n 22

22n22222n 4222n 22

n2

322n 32n 2n

Thay (3.20)-(3.23) vào phương trình (3.40) ta thu được:



(3.41)

Giải phương trình (3.41) ta thu được các giá trị tối ưu của β như sau:

n (1)  2

4

2

2

2 4

n n(1)

2 2 2

4

2



2 2 2

1

2

2  2



1,opt (3.42)

n (1)  2

4

2 2 2 4

n n(1)

2 2 2

4

2



2 2 2

1

2

2  2

2,opt 

(3.43)

Thay β=β1,opt và β=β2,opt vào biểu thức của hàm khuếch đại (3.27) ta thu được giá trị của hàm khuếch đại tại hai điểm cố định S và T.

A



1

B1 B2B3

S (3.44)

A



1

B1 B2B3

T (3.45)

trong đó

4n2(2 1)24 2222n 4

1

B  (2  1)

2

3

B 2242n  (222n 1)2 22n B 2 (2  2)

Theo Den Hartog [29], muốn đồ thị của hàm khuếch đại biên độ A không thay đổi lớn trong khoảng giữa hai đỉnh thì trước hết cần phải cho hai điểm S và T có độ cao bằng nhau, nghĩa là:

A2 A4

A2 A4

A A (3.46)

S T 1 2

Thay (3.20)-(3.23) vào phương trình (3.46), sau đó giải phương trình ta thu được tham số tối ưu của α như sau:



(3.47)

opt n 1 2 

Tiếp theo ta tìm hệ số cản ξ để đường cong biên độ-tần số đạt cực đại tại các điểm cố định S và T.

Để thỏa mãn điều kiện này ta có :

A 0





Từ phương trình (3.27) ta có:

A2 A2 A22 A2 A22

3 4 1 2

Đạo hàm hai vế của phương trình (3.49) theo β và giải ra nghiệm ξ2

(3.48)

(3.49)

A2 A A3 AA2 A A

A1

2 

3 3 1 

A2 A A4 AA2 AA

A2

(3.50)

4 

4 

2 

Thay điều kiện (3.48) vào phương trình (3.50) ta có:

A2 A

A3 A

A1

2 

3 1 

A2 A

A4 A

A2

(3.51)

4 2 

Thay các giá trị tối ưu α = αopt và β1 =β1,opt trong các phương trình (3.42), (3.47) vào phương trình (3.51) ta thu được:

A1 A1 A2 A3 A3

2 

1 A A2 A2 A

A4

(3.52)

2

4



opt , 1,opt

Tương tự thay các giá trị tối ưu α = αopt và β2 =β2,opt trong các phương trình (3.43), (3.47) vào phương trình (3.51) ta thu được:

A1 A1 A2 A3 A3

2 

2 A A2 A2 A

A4

(3.53)

2 

4

opt ,

2,opt

Theo Brock [24] tỷ số cản nhớt tối ưu ξopt được xác định như sau:

opt

* 

(3.54)

2 2

1 2

2

2

2

3

2n(1 2)

Thay (3.52) và (3.53) vào (3.54) ta thu được tỷ số cản tối ưu là:

opt

* 

(3.55)



Như vậy khi trục máy chịu tác động của mô men kích động điều hòa, thì các tham số tối ưu của bộ hấp thụ dao động xoắn DVA được xác định bằng phương pháp điểm cố định (các bước tính toán, biến đổi được lập trình tự động trên phần mềm Maple 2016) thu được các kết quả dưới dạng giải tích như sau:





2  2

1,2,opt 

1

4n2(21)24 2222n 4

n(2 1)22 2 2



opt 

2

2

3

2n(1 2)

opt 

n 12 

3.2. Xác định tham số tối ưu trong trường hợp trục máy chịu kích động ngẫu nhiên

Với trường hợp tính toán tham số tối ưu của bộ hấp thụ động lực DVA khi trục máy chịu tác dụng của kích động ngẫu nhiên, trong luận án này tác giả sử dụng phương pháp cực tiểu mô men bậc hai và phương pháp cực đại độ cản tương đương.

Phương pháp cực tiểu mô men bậc hai

Phương pháp cực tiểu mô men bậc hai áp dụng cho cơ hệ chịu tác động của mô men kích động ngẫu nhiên ồn trắng M(t) có mật độ phổ Sf .

Từ phương trình vi phân dao động dạng ma trận (3.5) ta đưa về phương trình trạng thái:

y (t) By(t) H f M (t)

trong đó:

(3.56)

T

y(t) là véc tơ trạng thái ứng với các đáp ứng của hệ và được xác định như sau:

y(t) a

a

(3.57)

Hf là véc tơ định vị của kích động [47]

1 T

H fM (t ) 0 M F 

(3.58)

Thay (3.9) và (3.12) vào phương trình (3.58) ta thu được véc tơ định vị của kích động

Hf:

0 

0 





 1 

H f 

Jr

(3.59)



1 

J 

r 

Ma trận hệ thống B được xác định như sau [11], [60] :

B 

0 E 

(3.60)



-M-1K -M-1C

Trong (3.60), E là ma trận đơn vị.

Thay (3.9), (3.10) và (3.11) vào phương trình (3.60) ta thu được ma trận hệ thống B như sau:

 0 0 1 0 

 0 0 0 1 



B 2

n222

0 n

2 

s s s 

2

12 n222

12 n222 

s



0

s 2 2 

s





Ma trận mô men bậc hai P là nghiệm của phương trình ma trận Lyapunov [67]

(3.61)

H H

f

f f

BP + PBT + S T = 0

(3.62)

Các thành phần của ma trận P được xác định bằng cách giải phương trình (3.62).

P11 P12 P13 P14 

P P P P 

P 

21 22 23 24 

(3.63)

P31 P32 P33 P34 

P P P P 

trong đó:

41 42 43 44 

1

S n244122n n24(12) 222(2 2) 4

f

r r s

P11 2

P



1 Sf

m243n24



(3.64)

r r s

22 2 m242n3

(3.65)

f

P33 

S (424n244n224n22  2222n 4 ) 2n2m244

s r r

(3.66)

P44

1Sf

r r s

2 m242n(3.67)

P P 1 S f

12 21 2

P13 P31  0

n22(21) 2

r r s

m2422n3

(3.68)

(3.69)

P P

1Sf

r r s

14 41

2 m2422

(3.70)

P P S f

r r s

23 32

224m22

(3.71)

P24

P

P42  0

s r r

f

P 

S (22n 2 )

(3.72)

(3.73)

34 43

2n24m22

Ta nhận thấy rằng ma trận mô men bậc hai P là ma trận đối xứng. Mô men bậc hai của chuyển dịch của hệ chính là thành phần P11.

Các tham số tối ưu được tìm làm tối ưu mô men bậc hai của đáp ứng hệ chính P11 [67]. Điều kiện cực tiểu là:

P11  0



P11  0



(3.74)

(3.75)

Thay (3.64) vào (3.74) và (3.75) ta thu được hệ phương trình sau:

S f (3C1 C2 )  0 2C3

S f (C1 C4 )  0 2C3

trong đó:

(3.76)

(3.77)