Cở Sở Lý Thuyết Phương Pháp Phần Tử Hữu Hạn Nguyên Tử

CHƯƠNG 2 TÍNH TOÁN DAO ĐỘNG CỦA TẤM VÀ

ỐNG NA NÔ SỬ DỤNG MÔ HÌNH PHẦN

TỬ HỮU HẠN NGUYÊN TỬ

2.1 Cở sở lý thuyết phương pháp phần tử hữu hạn nguyên tử

2.1.1 Thiết lập và giải phương trình trong AFEM

i i

Việc thiết lập và giải phương trình trong phương pháp phần tử hữu hạn nguyên tử đã được trình bày trong tài liệu [1, 71], cụ thể xét một hệ N nguyên tử. Gọi ro, r tương ứng là véc

tơ vị trí của nguyên tử i ban đầu và sau khi chuyển vị trong không gian,

u r rolà

i i i

i i

chuyển vị của nguyên tử i , rij rj ri là véc tơ nối giữa hai nguyên tử i, j . u , f tương ứng

là điều kiện biên chuyển vị và ngoại lực tác dụng lên nguyên tử i .

Khi đó tổng năng lượng ET

của hệ sẽ bằng nội năng của hệ trừ đi lượng cân bằng với

công của ngoại lực như sau [1, 75]:

ET r E rfi .ri , (2.1)

i1

trong đó:

r r ,r ,..., r

Tlà véc tơ vị trí của hệ và

E E r 

là nội năng hay thế năng

1 2 N

tương tác của hệ N nguyên tử.

Khi hệ ở trạng thái cân bằng, năng lượng đạt giá trị cực tiểu nên đạo hàm bậc nhất của tổng năng lượng của hệ khi đó phải bằng không. Ta có:

ET  0

r

(2.2)

Khai triển chuỗi Taylor hàm năng lượng ET

quanh vị trí cân bằng ban đầu

1 2

roro,ro,..., roT

ta có [71]:

ET r ET

roET





r

r ro

.u 1uT

2 E

rr

r ro

.u  ,

(2.3)

trong đó u r ro

là chuyển vị đủ nhỏ quanh vị trí cân bằng ro. u càng nhỏ khai triển

gần đúng (2.3) sẽ càng chính xác.

Thế phương trình (2.3) vào (2.2) chú ý bỏ qua vô cùng bé bậc cao ta có:

E E 2 E

. (2.4)

T T T

.u  0

r r

r ro

rr o

r r

Biến đổi phương trình (2.4) ta được:

Ku P , (2.5)

trong đó:

P ET

r

r ro

f 

E

r

rro

(2.6)

là lực của hệ ở trạng thái chưa cân bằng. Thành phần này sẽ tiến tới 0 khi hệ tiến tới vị trí cân bằng mới.

2 E

(2.7)

rr

rro

rr

r ro

là ma trận độ cứng của hệ ở trạng thái cân bằng ban đầu.

Quá trình tính toán thiết lập phương trình AFEM nêu trên được tác giả lập trình trên phần mềm Matlab.

2.1.2 Phần tử trong AFEM

Trong một hệ các nguyên tử, có thể coi mỗi một nguyên tử chỉ tác động qua lại chủ yếu với những nguyên tử gần với chúng, hình thành nên nhóm nguyên tử tương tác lân cận. Như vậy có thể hiểu rằng một cấu trúc nguyên tử là bao gồm rất nhiều nhóm nguyên tử tương tác lân cận. Với phương pháp phần tử hữu hạn thang nguyên tử (AFEM) mỗi nguyên tử trong hệ được coi là một nút và mỗi nhóm nguyên tử tương tác lân cận trong hệ lúc này được coi là các phần tử. Các nghiên cứu đã chỉ ra rằng các cách xây dựng phần tử trong AFEM có thể được phân chia làm hai nhóm là: xây dựng phần tử dựa trên hàm thế năng sử dụng và xây dựng phần tử dựa trên cấu trúc của hệ nguyên tử.

2.1.2.1 Xây dựng phần tử dựa trên hàm thế

Theo cách xây dựng phần tử dựa trên hàm thế năng, người ta sử dụng một phần tử m nút để mô tả cho các thành phần của hàm thế.

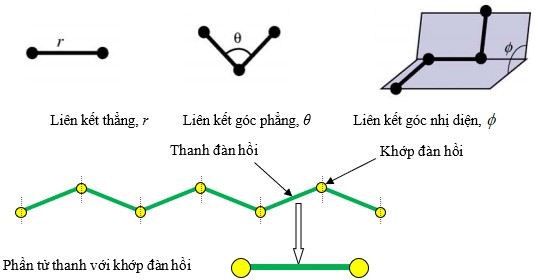
Hình 2.1 Kiểu phần tử thanh với khớp đàn hồi ba chiều mô phỏng liên kết trong ống SWCNT, nguồn [1, 111].

Ví dụ như Wang cùng cộng sự [126, 127] đã dùng một phần tử hữu hạn là một thanh có hai nút, mỗi nút là một nửa khớp đàn hồi có bậc tự do tịnh tiến và góc xoay như hình 3.4 để mô phỏng: liên kết thẳng, liên kết góc phẳng và liên kết góc nhị diện. Sun và Zhao [107] đã sử dụng kiểu phần tử này mô tả thế năng biến dạng dài, thế năng biến dạng góc và thế năng biến dạng xoắn để tính toán đặc trưng cơ học của SWCNT.

Lutz Nasdala và Gerald Ernst [82] đã phát triển phần tử hữu hạn gồm bốn nút để mô hình hóa cho thế năng xoắn DREIDING (hình 3.5).

Hình 2.2 Phần tử 4 nút được phát triển bởi Lutz Nasdala và Gerald Ernst [1, 82]

Zhang [132] đã đưa ra phần tử hữu hạn 6 nút để mô hình hóa thế năng thế hệ thứ hai của Brenner (hình 2.6).

Hình 2.3 Phần tử 6 nút mô hình hóa thế năng thế hệ thứ hai của Brenner [1, 132].

Tóm lại, việc xây dựng phần tử dựa trên hàm thế trong trường hợp này phụ thuộc trực tiếp vào hàm thế được chọn. Do đó, các vật liệu khác nhau nhưng sử dụng chung một dạng hàm thế thì ta cũng chỉ cần dùng một kiểu phần tử chung để mô phỏng chúng.

2.1.2.1 Xây dựng phần tử dựa trên cấu trúc nguyên tử

Phần tử hữu hạn trong trường hợp này bao gồm một nguyên tử trung tâm cùng với tất cả các nguyên tử khác nằm trong phạm vi tương tác với nguyên tử trung tâm đó. Cách xây dựng phần tử này năm 2004 đã được Liu cùng các đồng nghiệp đề xuất [71]. Khi đó các vật liệu khác nhau sẽ phải dùng các phần tử khác nhau để mô phỏng.

Hình 2.4 Phần tử khi lấy một nút làm trung tâm dùng cho mô hình: a) ống SWCNT; b) kim cương [1].

Ví dụ xét trong cùng một bán kính tương tác, mỗi phần tử trong ống cácbon na nô đơn lớp có 10 nguyên tử (1 nguyên tử trung tâm có 3 nguyên tử gần nhất và 6 nguyên tử gần thứ hai), trong khi kim cương là 17 nguyên tử (1 nguyên tử trung tâm có 4 nguyên tử gần nhất và 12 nguyên tử gần thứ hai) như hình 2.4.

Trong cách xây dựng phần tử này ta thấy không liên quan tới một dạng hàm thế cụ thể nào. Hay nói cách khác với cùng một cấu trúc của một vật liệu, ta vẫn chỉ chọn một kiểu phần tử duy nhất để mô phỏng cho một hàm thế bất kỳ. Dễ thấy phần tử trong trường hợp

này sẽ có khá nhiều nguyên tử (nút). Các phần tử trùng lặp nhau rất nhiều nút, dẫn tới việc tính toán ma trận phần tử và ghép nối ma trận tổng sẽ khó khăn. Để tránh điều này, ma trận độ cứng của mỗi phần tử lúc này khác FEM truyền thống ở chỗ tiêu điểm là nút trung tâm, thể hiện qua việc tất cả các đạo hàm bậc hai đều ít nhất một lần đạo hàm theo biến của tọa độ nút trung tâm, các thành phần khác bằng không. Điều này đảm bảo, các phần trùng nhau, lặp lại giữa các phần tử vẫn chỉ được tính một lần tới ma trận tổng thể. Một lợi thế khác là việc ghép nối ma trận tổng thể rất dễ dàng vì hàng thứ i trong ma trận tổng được xác định duy nhất từ ma trận phần tử có nút i là trung tâm. Tuy vậy việc xác định thế năng tương tác của phần tử trước khi tính ra ma trận độ cứng phần tử trong trường hợp này là không hề đơn giản.

Tuy có nhiều cách xây dựng phần tử khác nhau trong AFEM, nhưng tất cả đều cho ra chính xác ma trận độ cứng tổng thể từ đạo hàm bậc hai của hàm thế năng vì cả hai đều không sử dụng hàm dạng. Chúng chỉ khác nhau ở kiểu phần tử sử dụng. Do đó, nếu cùng sử dụng cùng một dạng hàm thế năng, cả hai cách xây dựng phần tử nêu trên đều cho ra kết quả tương tự. Nói cách khác, với một hệ xác định, khi ta chọn các kiểu phần tử khác nhau sẽ dẫn tới ma trận độ cứng phần tử khác nhau nhưng khi ghép nối lại sẽ cho ra một ma trận độ cứng tổng thể của hệ không đổi. Có nghĩa là trong AFEM không còn khái niệm chia lưới mịn hay không mịn. Điều này có thể giải thích là do trong AFEM vị trí các nút không thay đổi, vì nó chính là vị trí các nguyên tử trong hệ, chỉ phụ thuộc vào cấu trúc nguyên tử đang xét. Trong khi đó, việc chia lưới, chọn phần tử trong FEM truyền thống lại rất linh hoạt, và vị trí các nút trong hệ khi dùng FEM sẽ thay đổi theo sự chia lưới phần tử. Kết quả thu được trong FEM cũng ít nhiều bị ảnh hưởng bởi sự chia lưới thô hay mịn đó. Thêm một sự khác biệt nữa giữa AFEM và FEM là các phần tử trong FEM truyền thống chỉ có nút và biên chung. Trong khi AFEM, các phần tử gối lên nhau, trùng nhau một phần trong không gian.

2.1.2.3 Phần tử sử dụng trong luận án

Trong luận án này, tác giả đã sử dụng dạng phần tử được xây dựng dựa trên hàm thế là phần tử biến dạng dài hai nút và phần tử biến dạng góc ba nút [1]. Ưu điểm của việc sử dụng dạng phần tử được xây dựng dựa trên hàm thế năng là thuận tiện cho việc tính thế năng và thiết lập ma trận độ cứng phần tử. Hơn nữa, chỉ cần xây dựng một lần duy nhất mô hình phần tử hữu hạn để mô phỏng cho nhiều vật liệu khác nhau khi sử dụng chung một dạng hàm thế năng.

2.2 Mô hình phần tử hữu hạn nguyên tử với hàm thế điều hòa

2.2.1 Thông số hàm thế điều hòa

Theo cách tiếp cận tuyến tính, thế năng biến dạng dài giữa hai nguyên tử có thể được biểu diễn theo công thức:

E 1k l l 2, (2.8)

ij 2 r ij o

trong đó

lij

là khoảng cách giữa hai nguyên tử

i, j . khi hệ ở trạng thái cân bằng thì

lij lo . k

là tham số lực biến dạng dài. Hàm thế điều hòa cho biến dạng dài (2.8) chỉ phù

hợp khi hệ có biến dạng nhỏ.

Thế năng biến dạng góc giữa ba nguyên tử có thể được biểu diễn như sau:

E 1k 2, (2.9)

ijk 2 ijk o

trong đó ijk

là góc có đỉnh là nguyên tử j tạo bởi hai liên kết thẳng ji và jk . Khi hệ ở vị

trí cân bằng thì ijk o . Hàm thế điều hòa dạng này cũng chỉ phù hợp khi hệ có biến dạng nhỏ.

Trong luận án này, các-bon, BN, SiC là các vật liệu được chọn để mô phỏng. Chúng là các tấm, ống vật liệu na nô có cấu trúc dạng lục giác phẳng đơn lớp nên thông số kích thước

duy nhất cần được xác định là chiều dài liên kết l ở vị trí cân bằng ban đầu (hình 1.2a).

Các thông số hằng số lực trong hàm thế và chiều dài liên kết chi tiết trong bảng 2.1.

l của các vật liệu được nêu

Bảng 2.1 Các hằng số lực và chiều dài liên kết ban đầu của các vật liệu graphene, BN,

SiC ở nhiệt độ không độ Kelvin [1]

Vật liệu

Nguyên tử 1	Nguyên tử 2	Ce r kcal/(mol.Å2)	Ce 121 kcal/(mol.rad2)	Ce 212 kcal/(mol.rad2)	l0 Å
Các-bon	C	C	1051	195	195	1,42
BN	B	N	856	95	191	1,45
SiC	Si	C	447	155	105	1,77

Có thể bạn quan tâm!

Xem toàn bộ 133 trang tài liệu này.

Trong đó chiều dài liên kết ban đầu được lấy từ tài liệu tham khảo [101]; các hằng số lực của mô hình vật liệu graphene được tham khảo từ tài liệu [20], của vật liệu BN tham khảo từ tài liệu [60]; hằng số lực biến dạng góc trong mô hình vật liệu SiC được tham khảo từ tài liệu [97] còn hằng số lực biến dạng dài của SiC được tham khảo từ tài liệu [41].

2.2.2 Mô hình cơ học phân tử

Bonded

Nonbonded

Thế năng tương tác giữa các nguyên tử gồm thế năng tương tác liên kết ( E ) và thế năng tương tác phi liên kết ( E ) có thể được biểu diễn như sau [1, 3, 64]:

E E E

E E

, (2.10a)

Bonded r



E E

E , (2.10b)

Nonbonded vdw el

trong đó

E, E, Evdw

và Eel

tương ứng là thế năng đến từ biến dạng xoắn, đảo liên kết, lực

van der Waals và tương tác điện từ được bỏ qua trong nghiên cứu của luận án này. Do đó thế năng của hệ còn lại là:

E Er

E

. (2.10c)

Trong đó

E là thế năng biến dạng dài và E

là thế năng biến dạng góc. Ở biến dạng nhỏ

r 

chúng thường được mô tả bởi dạng hàm điều hòa như sau:

M e e 2

ErCrlij

e1

, (2.11)

N e e 2

ECijk ijk 

e1

, (2.12)

trong đó:

l

ijk

e là biến dạng dài của liên kết thẳng thứ e giữa hai nguyên tử i và nguyên tử j , e là

biến dạng góc giữa hai liên kết thẳng ji và jk (hình 2.5).

M và N tương ứng là tổng số biến dạng dài và biến dạng góc của hệ.

Ce và C e là hằng số lực tương ứng cho biến dạng dài và biến dạng góc.

r ijk

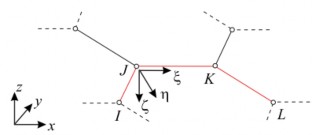
HìHìnnhh 2.52.5 MMôô hìnhhình haihai kkiểuiểu phầnphần ttửử:: a)a) phầnphần tửtử biếnbiến dạngdạng dàidài lvà biến dạng dài l ;

ij ij

ijk

b) phần tử biến dạng góc và biến dạng góc [1].

ijk

Với những tấm vật liệu cấu tạo bởi hai loại nguyên tử sẽ có hai giá trị C e

tương ứng phụ

thuộc vào kiểu nguyên tử ở đỉnh của góc có biến dạng. Trong hình 2.5b, nguyên tử i và k

là cùng loại. Các ma trận độ cứng được thiết lập dựa trên hàm thế điều hòa được tham khảo từ tài liệu [63].

2.2.3 Ma trận độ cứng phần tử

Trong mô hình phần tử hữu hạn nguyên tử (AFEM), nguyên tử và chuyển vị nguyên tử được coi là các nút và chuyển vị nút tương ứng. Phần tử biến dạng dài và biến dạng góc được mô hình hóa thành bởi phần tử biến dạng dài hai nút và phần tử biến dạng góc ba nút như trong hình 2.5. Cần lưu ý rằng trong trong các phần mềm phần tử hữu hạn thì các phần tử lò xo dễ dàng mô tả phần tử biến dạng dài theo phương trình (2.11). Trong khi đó, rất khó để mô tả phần tử biến dạng góc, xem ở phương trình (2.12) do sự quay của các-bond liên quan. Ở đây, năng lượng biến dạng dài và biến dạng góc được mô tả thành đa thức bậc hai của chuyển vị của các nguyên tử. Nó cho phép xây dựng một cách rõ ràng các ma trận độ cứng phần tử.

2.2.3.1 Ma trận độ cứng của phần tử biến dạng dài hai nút

Ma trận độ cứng phần tử biến dạng dài hai nút được trình bày trong tài liệu [1] cụ thể theo hình 2.5a thế năng biến dạng của một phần tử hai nút sẽ là:

Ee1Cele2. (2.13)

r 2 r ji

Xét tương tác giữa hai nguyên tử i và j . Khoảng cách giữa chúng là e

có thể được

biểu diễn thông qua tọa độ xi,yi,zicủa nguyên tử i và tọa độ x j, y j, z jcủa nguyên tử

j như sau:

le2x x 2y y 2z z 2. (2.14)

ji i j i j i j

Vi phân hai vế phương trình (2.14), ta có:

le le

x x

x x

y y

y

y

z z

z

z

. (2.15)

ji ji i j i j i j i j i j i j

Đặt xi q1,yi q2 ,zi q3 và xj q4 ,yj q5 ,z j q6

là các chuyển vị của nguyên

tử i và j theo các trục

x, y và z tương ứng. Phương trình (2.15) trở thành:

le 1 x q q

y q q z

q q , (2.16)

ji e ij 1 4

ij 2 5

ij 3 6 

trong đó:

xij xi xj ,

yij yi yj ,

zij zi z j . (2.17)