Tổng Hợp Các Thông Số Của Tấm Và Ống Vật Liệu Na Nô [1]



Xi xi



Yi R sin yi / R

(1.5)

Z R cos y / R1

ii

trong đó, R là bán kính ống được xác định như sau:



n2 mn m2

R  22

. (1.6)

Như vậy, một ống na nô được xác định về kích thước khi biết các thông số là cặp chỉ số

n, m

và chiều dài ống L, các thông số khác được tính phụ thuộc vào n, m

như trong

bảng 1.1.

Bảng 1.1 Tổng hợp các thông số của tấm và ống vật liệu na nô [1]

Ký hiệu

Tên gọi, mô tả

Công thức xác định

Chiều dài liên kết ban đầu

Khoảng cách giữa 2 nguyên tử gần nhất.



Góc liên kết

 32 l 2 

arccos Low buckled o

 2l 2 

Chiều dài véc tơ đơn vị

a a a  3l 2 2 

1 2 o Low buckled

a1,a2

Véc tơ đơn vị trong hệ tọa độ

x, y 

a 1 a, 3 a  , a 3 a, 1 a 

1 2 2 2 2 2 



Véc tơ xoắn

Ch OA na1 ma2

n, m là các số nguyên.

Đường kính ống

C a

D h n2 mn m2



Có thể bạn quan tâm!

Xem toàn bộ 133 trang tài liệu này.

Bên cạnh cấu trúc lục giác lý tưởng như trên, tấm và ống vật liệu sau khi tổng hợp được cũng thường xuất hiện các khuyết tật. Trong đó luận án này nghiên cứu sinh có xét đến khuyết tật mất nguyên tử liền kề của tấm vật liệu na nô hình 1.6.

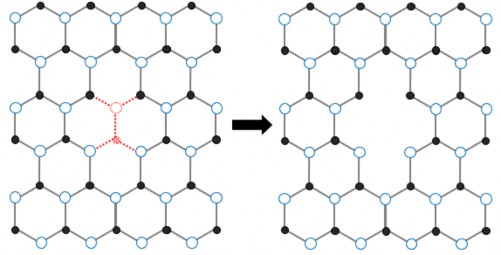
Hình 1.6 Khuyết tật mất nguyên tử liền kề của tấm vật liệu na nô lục giác [1]

1.3 Tổng quan về nghiên cứu dao động tự do của kết cấu na nô lục giác

Hashemnia và cs [54] và Ávila và cs [15] đã phân tích dao động của tấm graphene dựa trên cấu trúc na nô sử dụng mô phỏng cơ học phân tử, trong đó tương tác giữa các nguyên tử được mô tả bởi các thanh chịu kéo (nén), uốn và xoắn. Gupta và Batra [50] và Chowdhury và cs [31] đã tính toán tần số dao động tự do của tấm graphene sử dụng mô hình động lực học phân tử MD. Arghavan và Singh [9, 10, 54] sử dụng mô hình cấu trúc nguyên tử để xác định tần số riêng và dạng dao động riêng của tấm graphene có hình dạng khác nhau, chịu những điều kiện biên khác nhau. Mohammadi và cs [78] đã nghiên cứu ảnh hưởng của tải trọng ban đầu trong mặt phẳng lên tần số dao động của tấm graphene tròn thông qua lý thuyết tấm liên tục không cục bộ. Murmu và cs [81] đã nghiên cứu dao động của tấm graphene dưới ảnh hưởng của từ trường. Sử dụng phương pháp vi phân cầu phương và lý thuyết áp điện Arani và cs [7] đã khảo sát dao động phi tuyến của tấm BN. S Ajori [2] cùng cộng sự mô phỏng dao động của ống CNT sử dụng phương pháp động lực học phân tử (MD). Ansari cùng đồng sự [6] sử dụng phương pháp động lực học phân tử (MD) khảo sát dao động tự do xoắn của ống BN

Nhìn chung, các vật liệu na nô mới được phát hiện gần đây vẫn chưa có nhiều nghiên cứu dao động về kết cấu của những vật liệu này.

1.4 Một số phương pháp tính toán vật liệu na nô

Bên cạnh những phương pháp thực nghiệm phức tạp và đắt tiền ở thang na nô [8, 28, 42], có ba phương pháp chính để mô hình hóa kết cấu na nô: (a) mô hình nguyên tử (atomistic modeling), (b) mô hình lai nguyên tử - cơ học môi trường liên tục (hybrid atomistic- continuum mechanics) và (c) mô hình cơ học môi trường liên tục (continuum mechanics). Mô hình hóa nguyên tử bao gồm các phương pháp như động lực học phân tử cổ điển (MD), động lực học phân tử tight-binding (TBMD) và lý thuyết mật độ phiếm hàm (DFT) [8, 28, 42, 66]. Mô hình lai nguyên tử - cơ học môi trường liên tục cho phép kết hợp trực tiếp thế năng tương tác nguyên tử vào phân tích liên tục. Điều này được thực hiện bằng cách cân bằng thế năng phân tử của vật liệu cấu trúc na nô với năng lượng biến dạng cơ học của phần tử trong mô hình liên tục [65]. Cơ học liên tục bao gồm các lý thuyết dầm, tấm và vỏ cổ điển. Phương pháp cơ học liên tục ít tốn kém tài nguyên tính toán hơn so với hai cách tiếp cận trên và công thức của chúng tương đối đơn giản. Những lợi thế này làm cho mô hình liên tục được sử dụng như một cách thay thế để mô phỏng một số ứng xử trong các kết cấu na nô như mất ổn định [38, 124], truyền sóng [69, 123] và dao động tự do [17, 55, 61, 68, 110]. Vì lý thuyết cơ học liên tục dựa trên giả thuyết liên tục trong mô hình hóa, việc kiểm chứng kết quả bằng lý thuyết liên tục từ các kết quả có sẵn từ mô hình nguyên tử hoặc kết quả thực nghiệm là không thể thiếu được khi áp dụng lý thuyết này trong phân tích các kết cấu làm từ vật liệu na nô.

Có hai nhóm phương pháp thường được sử dụng để tính toán, mô phỏng các đặc trưng của vật liệu na nô nói chung và vật liệu na nô cấu trúc lục giác nói riêng. Nhóm phương pháp thứ nhất là ở cấp độ electron và nhóm thứ hai là cấp độ nguyên tử. Nhóm phương pháp ở cấp độ electron có phương pháp lý thuyết hàm mật độ (DFT), ở cấp độ nguyên tử thì có phương pháp mô phỏng động lực phân tử (MD). MD và DFT là hai phương pháp chuẩn mực được sử dụng nhiều trong các nghiên cứu lý thuyết hoá học, vật lý và khoa học vật liệu. Có rất nhiều các công trình nghiên cứu sử dụng hai phương pháp này. Nhiều nghiên cứu, phương pháp ra đời sau này thường lấy DFT và MD làm chuẩn để so sánh, kiểm nghiệm và đánh giá tính tin cậy.

Trong luận án này, tác giả sẽ kế thừa, phát triển phương pháp phần tử hữu hạn nguyên tử (AFEM) hay còn được gọi là phương pháp phần tử hữu hạn-động lực phân tử để khảo sát, tính toán các đặc trưng về dao động cho tấm và ống na nô có cấu trúc lục giác. Kết quả thu được từ AFEM cũng được so sánh chủ yếu với kết quả từ DFT, MD để đánh giá độ tin cậy của phương pháp cũng như mô hình.

1.4.1 Phương pháp lý thuyết mật độ phiếm hàm

Phương pháp cho kết quả chính xác nhất là phương pháp lý thuyết hàm mật độ vì nó dựa trên cơ học lượng tử. Nhược điểm của phương pháp này là khối lượng tính toán rất lớn [1, 95], đòi hỏi tài nguyên thiết bị nhiều vì các phương pháp dựa trên cơ học lượng tử tập trung đi tìm nghiệm của phương trình Schrödinger [1].

Tổng quát, trạng thái của một hệ hạt có thể được xác định thông qua hàm sóng thỏa

mãn phương trình Schrödinger như sau:

HE, (1.7)

trong đó H là toán tử Hamilton của hệ cơ học lượng tử. là hàm đặc trưng năng lượng ứng với trị số đặc trưng năng lượng E .

Trong cơ học lượng tử, một xấp xỉ thường được dùng là xấp xỉ Born-Oppenheimer, nó

giả thiết là các electron luôn ở trạng thái bền, chuyển động của chúng nhanh hơn nhiều so với chuyển động của các hạt nhân. Dựa vào đó, chuyển động của các electron có thể được xem xét riêng, như thể coi các hạt nhân khi đó đang đứng yên. Khi đó với một hệ có N electron, toán tử H cho mỗi electron được biểu diễn như sau:

H 12 1r , (1.8)

i 2i

j i ri rj

trong đó, thành phần

1 2

2 i

là toán tử động năng dựa trên hàm sóng electron. Thành phần

ri rj

1

j i

là toán tử tương tác giữa các electron với nhau, phần còn lại ri

là toán tử

tương tác giữa electron và hạt nhân. Tổng toán tử của N electron khi đó là:

H Hi , (1.9)

và trạng thái của các electron có thể biết thông qua giải phương trình trị riêng:

1 2

H,,...

E,,...,,...

(1.10)

1 2

trong đó i

là trạng thái riêng tương ứng với một phương trình trị riêng:

Hi

E. (1.11)

i i i

Để tìm lời giải chính xác cho phương trình (1.11) là rất khó, do đó có nhiều phương pháp xấp xỉ được đưa ra. Trong đó có hai phương pháp hay dùng hiện nay là phương pháp xấp xỉ Hartree-Fock và lý thuyết hàm mật độ (Density Functional Theory-DFT). Phương pháp

Hartree-Fock có những mặt hạn chế nên kết quả thu được cũng chưa thật sự phù hợp với thực nghiệm. Phương pháp DFT ra đời đánh dấu một bước tiến mới trong lĩnh vực tính toán mô phỏng [96].

DFT là một lý thuyết được dùng để mô tả các tính chất của hệ electron trong nguyên tử, phân tử, vật rắn, … trong khuôn khổ của lý thuyết lượng tử. Trong DFT, các tính chất của hệ N electron được biểu diễn qua hàm mật độ electron của toàn bộ hệ (là hàm của 3 biến tọa độ không gian) thay vì hàm sóng (là hàm của 3N biến tọa độ không gian). Vì vậy, lý thuyết hàm mật độ có ưu điểm lớn trong việc tính toán các tính chất vật lý cho các hệ cụ thể xuất phát từ những phương trình rất cơ bản của vật lý lượng tử. Nền tảng cơ bản của DFT là năng lượng ở trạng thái cơ bản là một hàm của mật độ electron, do đó về nguyên tắc có thể mô tả hầu hết các tính chất vật lý của hệ electron qua hàm mật độ. Năm 1964, Hohenberg và Kohn

[57] cho rằng trạng thái năng lượng của hệ electron đạt cực tiểu là một hàm của mật độ electron như sau:

E T r 

rr'drdr ' 

V r dr E

r , (1.12)

r r '



N XC 

trong đó hàm động năng T rlà một hàm của hàm mật độ electron. Thành phần thứ hai là thế năng tĩnh điện, thành phần thứ ba là thế năng của hạt nhân. Thành phần cuối cùng là hàm năng lượng tương quan. Một năm sau, Kohn và Sham nêu ra qui trình tính toán để thu được gần đúng mật độ electron ở trạng thái cơ bản trong khuôn khổ lý thuyết nêu trên, phương pháp của họ nói chung có liên quan tới phương pháp xấp xỉ mật độ địa phương. Sự thành công của phương pháp xấp xỉ mật độ địa phương cùng với khả năng tính toán ngày càng mạnh của công nghệ máy tính hiện đại tạo nên ứng dụng phổ biến của DFT. Nó đã được sử dụng rộng rãi và hiệu quả trong các ngành khoa học như: vật lý chất rắn, hóa học lượng tử, vật lý sinh học, khoa học vật liệu ... Kohn đã được ghi nhận những đóng góp của ông cho việc phát triển lý thuyết hàm mật độ bằng giải thưởng Nobel hóa học năm 1998.

Mô phỏng trong cơ học lượng tử cho kết quả rất tốt khi ứng dụng nghiên cứu các tính chất liên quan đến mật độ và phân bố điện tử. Tuy nhiên hạn chế của phương pháp này là chỉ mô phỏng cho hệ có số lượng nguyên tử nhỏ.

1.4.2 Mô phỏng động lực phân tử

Về cơ bản mô phỏng động lực phân tử (Molecular Dynamics – MD) là một phương pháp hạt bởi vì mục tiêu của MD là giải phương trình đặc trưng động lượng hạt dựa trên định luật 2 Newton như sau [72]:

i i

mr E r1,r2,...rNF ,

i  1, 2,...N

(1.13)

ri

trong đó mi , ri là khối lượng và tọa độ không gian của nguyên tử thứ i . E là thế năng của hệ được cho trước từ thực nghiệm.

Phương trình (1.13) có thể được rút ra từ hệ phương trình vi phân thường:

dpi

dt



dqi

dt

H

q

i , (1.14)

H

pi

với

qi , pi

là hệ tọa độ và mô men động lượng, H là toán tử Halminton có dạng:

N p2

H iE . (1.15)

i 2mi

Hệ gồm N nguyên tử thì phương trình trên là một hệ gồm N phương trình phi tuyến. Lời giải chính xác cho hệ đó là rất khó. Ta có thể tìm lời giải gần đúng qua việc chia các bước thời gian ∆t, sau mỗi bước thời gian đó, hệ các nguyên tử sẽ tới một trạng thái mới. Trạng thới mới được tính dựa trên các trạng thái trước đó nhờ vào các thuật toán, ví dụ như thuật toán Verlet. Việc chia bước thời gian càng nhỏ sẽ cho độ chính xác càng cao, nhưng ngược lại khối lượng tính toán tăng lên đáng kể. Do đó việc chọn bước thời gian tối ưu cần được quan tâm trong mô phỏng MD.

Như vậy, nếu biết được trạng thái ban đầu, và hàm thế năng của hệ ta hoàn toàn xác định được vị trí và động lượng của các nguyên tử ở các bước thời gian tiếp theo.

1.4.3 Phương pháp phần tử hữu hạn nguyên tử

Những phương pháp tính toán, mô phỏng thường được sử dụng như mô phỏng động lực phân tử (MD) và lý thuyết hàm mật độ (DFT) đều có ưu điểm là cho kết quả chính xác cao. Nhược điểm của hai phương pháp này chính là khối lượng tính toán lớn, đòi hỏi nhiều thời gian và tài nguyên thiết bị. Phương pháp áp dụng cho kết cấu vĩ mô như phương pháp phần tử hữu hạn truyền thống (FEM) không thể áp dụng cho các tính toán cấp độ nguyên tử trong trường hợp này vì kết cấu na nô là những hệ có hữu hạn các nguyên tử rời rạc. Trong khi đó, ứng xử của những kết cấu từ vật liệu thang vĩ mô đã hoàn toàn xác định và tích hợp trong FEM thông qua các mô hình phần tử đại diện như thanh, tấm, vỏ… chúng là những mô hình đã được tính toán từ các thí nghiệm thực tế như kéo, nén, uốn, xoắn.

Cần có một phương pháp khắc phục được nhược điểm của hai phương pháp trên trong khi vẫn có ưu điểm là cho kết quả tính toán chính xác. Phương pháp phần tử hữu hạn nguyên tử được đề xuất bởi Liu và cộng sự vào năm 2004 [71] (Atomistic finite element method hoặc Atomic-scale finite element method - AFEM). Một tên gọi khác của phương pháp này là phương pháp phần tử hữu hạn động lực phân tử. Phương pháp AFEM đã được sử dụng để tính toán, mô phỏng các kết cấu từ vật liệu cấu trúc na nô một cách hiệu quả thời gian gần đây [71, 75, 82, 83, 127]. Trong phương pháp này nguyên tử của hệ được coi là các nút và chuyển vị của các nguyên tử được xem như là các chuyển vị của các nút. Các phần tử trong AFEM được xây dựng để mô tả cho hàm thế năng. Từ hàm thế năng có thể xây dựng được ma trận độ cứng của các phần tử. Sau đó, ma trận độ cứng tổng thể được ghép nối từ các ma trận độ cứng phần tử giống như trong phương pháp phần tử hữu hạn truyền thống. Mối liên hệ giữa ngoại lực và chuyển vị của các nút cũng được mô tả bằng hệ phương trình đặc trưng. Nghiên cứu của Liu và cộng sự đã chứng minh khi dùng chung các thông số hàm thế thì phương pháp phần tử hữu hạn nguyên tử cho kết quả chính xác tương đương các phương pháp tính toán ở cấp độ nguyên tử như MD. Quá trình tính toán hội tụ sau ít bước lặp hơn của AFEM so với MD sẽ cho tốc độ tính toán nhanh hơn, tiết kiệm được thời gian và tài nguyên máy. Có được điều này là do AFEM sử dụng cả đạo hàm bậc nhất và đạo hàm bậc hai của hàm thế năng khi tính toán cực tiểu hóa năng lượng của hệ để tìm vị trí cân bằng, trong khi MD chỉ sử dụng đạo hàm bậc nhất của hàm thế năng [71]. Trong nghiên cứu này Liu chọn các phần tử dựa trên cấu trúc của nguyên tử bao gồm một nguyên tử làm trung tâm và tất cả các nguyên tử khác có tương tác với nguyên tử trung tâm này. Với cách chọn như vậy sẽ cho ra kết quả ma trận độ cứng cồng kềnh. Mặc dù Liu đã đưa ra phương pháp để ghép nối các ma trận độ cứng phần tử khá đơn giản nhưng để tính toán được ma trận của một phần tử gồm nhiều nguyên tử như trong trường hợp này lại không đơn giản. Nasdala và cộng sự [82, 83] đã đề xuất mô hình phần tử bốn nút để mô phỏng cho cả thế năng biến dạng uốn, xoắn và biến dạng dài giữa các nguyên tử. Wang và cộng sự đã đưa ra mô hình phần tử thanh thẳng với hai nửa khớp đàn hồi ở hai đầu, mỗi khớp có 6 bậc tự do như vậy phần tử

của Wang có 12 bậc tự do.

1.5 Kết luận chương

Sau phát hiện của Sumio Iijima về vật liệu các-bon là ống na nô các-bon đa lớp năm 1991 và ống na nô các-bon đơn lớp năm 1993. Đến nay đã có nhiều các vật liệu có cấu trúc tương tự khác được chứng minh tồn tại trên lý thuyết. Một vài vật liệu trong số đó đã được tổng hợp thành công

trên thực tế như SiC, BN, Si,... Các nghiên cứu tìm đặc trưng cơ, lý, hóa, dao động đã chứng minh rằng chúng có rất nhiều những đặc tính ưu việt, nhiều triển vọng để ứng dụng các vật liệu này vào trong thực tế, trên nhiều lĩnh vực như chế tạo linh kiện điện tử, cảm biến, máy tạo dao động, vật liệu na nô composite,...

Trong khi các phương pháp nghiên cứu bằng thực nghiệm còn nhiều hạn chế và đôi khi là không thực hiện được thì tính toán, mô phỏng số có nhiều ưu thế. Ngoài các phương pháp tính toán ở thang nguyên tử cho kết quả chính xác cao như mô phỏng động lực phân tử, lý thuyết hàm mật độ thì phương pháp phần tử hữu hạn thang nguyên tử (AFEM) lại khắc phục được nhược điểm khối lượng tính toán lớn của hai phương pháp trên. Kết quả là khi sử dụng AFEM sẽ tiết kiệm được thời gian tính toán và giảm chi phí cho tài nguyên máy.

Nghiên cứu sinh cùng người hướng dẫn nhận định phương pháp phần tử hữu hạn nguyên tử là phương pháp mới, còn nhiều điều có thể phát triển để áp dụng mô phỏng tìm đặc trưng dao động của các kết cấu từ vật liệu na nô. Luận án sẽ tập trung vào một số vật liệu mới được phát hiện như: boron nitride (BN), silicon carbide (SiC). Cụ thể, luận án sẽ đưa ra cách chọn phần tử đơn giản, phù hợp với hàm thế điều hòa để có thể tính toán ra ma trận độ cứng và ma trận khối lượng một cách thuận lợi nhất. Chi tiết hơn về phương pháp phương pháp phần tử hữu hạn nguyên tử cũng như việc thiết lập các phần tử, mô hình của luận án sẽ được trình bày trong phần tiếp theo.