p1t = C1 sin ω1t + α1; p2t = C2 sin ω2t + α2
Trở lại tọa độ suy rộng φ1, φ2 ta có
φ1t = C1 sin ω1t + α1+ C2 sin ω2t + α2φ2t = C1 sin ω1t + α1− C2 sin ω2t + α2
Các hằng số C1, C2, α1, α2 được xác định từ các điều kiện đầu φ10 = φ0, φ20 = 0 , φ 10 = 0 , φ 20 = 0.
Đạo hàm theo thời gian các hàm φ1, φ2 ta được
φ 1t = ω1C1 cos ω1t + α1+ ω2C2 cos ω2t + α2φ 21t = ω1C1 cos ω1t + α1− ω2C2 cos ω2t + α2
Từ các điều kiện đầu đã cho ta được hệ bốn phương trình xác định C1, C2, α1, α2
𝐶1 sin 𝛼1 + 𝐶2 sin 𝛼2 = 𝜑0
𝐶1 sin 𝛼1 − 𝐶2 sin 𝛼2 = 0
ω1C1 cos α1 + ω2C2 cos α2 = 0 ω1C1 cos α1 − ω2C2 cos α2 = 0
Từ hai phương trình thứ ba và thứ tư ta suy ra
cos α cos α 0 α α π
1 2 1 2 2
Từ hai phương trình đầu ta có
1
2C1 sin α1 = 2C2 sin α2 = φ0 → C1 = C2 = 2 φ0
Vậy dao động tự do của hệ hai con lắc có dạng
| ω1 ω2 | t cos | ω1 ω2 | t | |
| 2 | | | 2 | |
Có thể bạn quan tâm!
-
Hình Bài Tập 2 Hình 2.46 Hình Bài Tập 3 -
Phương Pháp Sử Dụng Phương Trình Lagrange Loại Ii. -
Đỗ Vòng Và Góc Xoay Của Đường Đàn Hồi Của Các Dầm Thẳng Có Tiết Diện Không Đổi. -
Phương Pháp Ma Trận Dạng Riêng (Ma Trận Cản Đặc Biệt) -
A Mô Hình Dao Động Bộ Tắt Chấn Động Lực Có Tính Đến Ma Sát Nhớt -
Dao Động Dọc Tự Do Của Thanh Đồng Chất Tiết Diện Không Đổi
Xem toàn bộ 182 trang tài liệu này.
φ t φ0 cos ω t cos ω t φ cos
1 2 1 2 0
| ω1 ω2 | t si | n | ω1 ω2 | t |
| 2 | | | 2 | |
φ t φ0 cos ω t cos ω t φ sin
2 2 1 2 0
Thí dụ 3.8 : Tính toán các tần số riên và dạng dao động riêng của mô hình dao động 3 bậc tự do như hình 3.8
x1
x2
x3
c
2c
c
2c
m m
m/2
Hình 3.8 Hình thí dụ 3.8
Lời giải : Biểu thức động năng và thế năng của hệ có dạng
T = 1 2 1
2 1 2
2 mx 1 + 2 mx 2 + 4 mx 3
1
Π = cx2 + c x 2 1 2
1
− x12 + c
2
x3 − x22 + cx2
3
Thế các biểu thức động năng và thế năng vào phương trình Lagrange loại II ta nhận được hệ phương trình vi phân dao động
m 0 0
x 1
3c −2c 0 x1 0
0 m 0
x 2+ −2c 3c −c x2 = 0
0 0 m 2
x 3
0 −c 3c x3 0
Phương trình tần số (Phương trình đặc trưng) có dạng
3c − ω2m −2c 0
−2c 3c − ω2m −c
= 0
0 −c
3c −
1
ω2m
2
Nếu ta đưa vào ký hiệu 𝜆 = 𝜔2 𝑚 thì phương trình đặc trưng có dạng
𝑐
−𝜆3 + 12𝜆2 − 39𝜆 + 24 = 0
Giải ra ta được
c
λ1 = 0,7985 → ω1 = 0,8936
m
c λ2 = 4,4549 → ω2 = 2,1107 m
c λ3 = 6,7466 → ω3 = 2,5974 m
Phương trình xác định các véc tơ riêng có dạng
3 − λ −2 0
−2 3 − λ −1
a1 0
a2 = 0
0 −1 3 − λ 2 a3 0
Từ phương trình thứ nhất ta suy ra
3 − λ ai− 2ai= 0 → ai= 2
a(i)
i 1 2
1 3 − λi 2
Từ phương trình thứ ba ta suy ra
6 − λ ai− 2ai= 0 → ai= 2
a(i)
i 1 2
3 6 − λi 2
2
Cho a(i) = 1 (i = 1, 2, 3) và thế các giá trị của λi vào các biểu thức trên ta nhận được ma trận dạng riêng
0,9085 −1,3747 −0,5338
𝐕 = 1 1 1
3.2.4 Các tọa độ chuẩn
0,3845 1,2944 −2,6789
Như đã biết bằng phép thế q = Vp (V là ma trận dạng riêng, p là véc tơ các tọa độ chính) ta có thể đưa phương trình vi phân dao động
M 𝐪 + C q = 0
về dạng vế trái tách rời nhau
µi p i + 𝛾ipi = 0 i = 1,2,…,n Trong đó µi và 𝛾i được xác định bởi các hệ thức
Do các phần tử của véc tơ vi của ma trận dạng riêng V được xác định sai khác một hằng số nhân, cho nên ta có thể chọn các véc tơ vi một cách thích hợp sao cho
1 0 … 0
𝐕𝐓 𝐌 𝐕 = 0 1 … 0 = 𝐄 (2.31)
… … … …
0 0 … 1
Ma trận dạng riêng được chọn như thế được gọi là ma trận dạng riêng chuẩn. Ta ký hiệu ma trận dang riêng chuẩn bằng Vn. Như thế nếu Vn là ma trận dạng riêng chuẩn thì ta có các hệ thức
1
2
ω2 0 … 0
𝐕𝐓 𝐌 𝐕 = 𝐄 ; 𝐕𝐓 𝐂 𝐕
= 𝐃
=0 ω2 … 0
𝐧 𝐧 𝐧
ω… … … …
n
0 0 … ω2
Bằng pháp thế q = Vn p ta có thể đưa phương trình
M 𝐪 + C q = 0
về dạng : E 𝐩 + 𝐃𝛚𝐩 = 𝟎
Các tọa độ chính p = [p1, p2,…,pn]T trong phép thế q = Vn p được gọi là các tọa độ chuẩn. Chú ý rằng các tọa độ chuẩn là các tọa độ chính đặc biệt. Ta vẫn sử dụng các ký hiệu pi để chỉ các tọa độ chuẩn. Bạn đọc cần chú ý đến chú giải trên để tránh nhầm lẫn sau này.
Nếu ta biết được ma trận dạng riêng
V = [v1, v2,…, vn] (2.32)
thì mà trận dạng riêng chuẩn được xác định bởi hệ thức
V 1 v , 1 v ,., 1 v
(2.33)
n α 1 α 2 α n
1 2 n
vTMv
i i
Trong đó các hằng số αi được xác định bởi công thức
μi
αi
(2.334)
Thí dụ 3.9: Hãy tính mà trận dạng riêng chuẩn của thí dụ 3.8. Cho biết m=10kg, c = 1000N/m
Lời giải: Từ ma trận dạng riêng V đã biết trong thí dụ 3.8 ta dễ dàng tính được
1
1
𝛼1 = ± 𝐯T 𝐌𝐯𝟏 = ±4,3581 (kg)2
1
2
𝛼2 = ± 𝐯T 𝐌𝐯𝟐 = ±6,1054 (kg)2
1
3
𝛼3 = ± 𝐯T 𝐌𝐯𝟑 = ±6,9808 (kg)2
Nếu chọn α1= 4,3581; α2 = 6,1054; α3 = 6,9808 thì ta có
1
α
Vn =
1
1
α
v1 ,
2
1
α
v2 ,
3
0,2085 −0,2252 −0,0765 v3= 0,2295 0,1630 0,1432
0,0882 0,2120 −0,3838
Nếu chọn α1= 4,3581; α2 = - 6,1054; α3 = - 6,9808 thì
1
α
Vn =
1
1
α
v1 ,
2
1
α
v2 ,
3
0,2085 0,2252 0,0765 v3= 0,2295 −0,1630 −0,1432
0,0882 −0,2120 0,3838
*Một vài trường hợp đặc biệt
Trong đoạn này giới hạn xét dao động tự do hệ hai bậc tự do. Phương trình vi phân dao động có dạng
m11&q&1 m12&q&2 c11q1 c12q2 0
m21&q&1 m22&q&2 c21q1 c22q2 0
(2.35)
Khi sử dụng các tọa độ chính hệ phương trình (2.35) đưa được về dạng
p 1 + ω2p1 = 0
1
2
p 2 + ω2p2 = 0
(2.36)
a) Trường hợp 1: ω1 = ω2 =ω. Khi đó nghiệm hệ phương trình (2.36) có dạng p1 = C1 sin(ωt + α1); p2 = C2 sin(ωt + α2) (2.37)
Cả hai tọa độ chính đều dao động điều hòa với cùng tần số ω. Từ hệ thức
q = V p
ta suy ra
q1 = A1sin (ωt + β1); q2 = A2sin (ωt + β2)
Trong trường hợp này cả hai tọa độ suy rộng đều thực hiện dao động điều hòa với cùng tần số ω. Nếu ta chọn tọa độ q1, q2 bất kỳ thì chúng cũng dao động điều hòa với tần số ω chung đó. Do đó phương trình dao động có dạng
q 𝟏 + ω2 q1 = 0 ; q 𝟐 + ω2 q2 = 0 (2.38)
1 2
b) Trường hợp 2: ω1 ≠ 0; ω2 = 0. Khi đó hệ phương trình (2.36) có dạng
1 1
&p&1 ω2p 0
&p&2 0
p1 C1 sin ω1t α1
p2 C2t C3
Như thế trong trường hợp ω1 ≠ 0; ω2 = 0 thì tọa độ chính p1 thực hiện dao động điều hòa với tần số ω1 còn tọa độ chính p2 hoặc luôn là hằng số (nếu C2 = 0) hoặc tăng lên vô cùng khi thời gian t tăng. Khả năng nào xảy ra phục thuộc vào các điều kiện đầu.
Nếu như ta chọn q1, q2 một cách tùy ý, thì từ các phương trình (2.10a) và (2.10b) ta có
c11 − m11 ω2+ v2c12 − m12 ω2= 0
2 2
c12 − m21 ω2+ v2c22 − m22 ω2= 0
2 2
Khi ω2 = 0, từ hai phương trình trên ta suy ra
2
v c11 c12
c12 c22
c12 = ± c11
c12
Bây giờ ta xét hệ cơ học thỏa mãn điều kiện trên. Ngoài ra ta còn giả thiết thêm c11 ≠ 0; c22 = 0; c12 = 0
Động năng và thế năng của hệ khảo sát có dạng
T 1m q&2 2m q&q& m q&2
2 11 1 12 1 2 22 2
Π 1 c q2
2 11 1
Thế vào phương trình Lagrange loại II ta được hệ phương trình vi phân m11q1+ m12q 2 + c11q1= 0
m12q1+ m22q 2 = 0
Hai phương trình này có thể viết lại dưới dạng như sau
2
&q& m12 &q&
m22
m2
m11 12 &q&+ c11q1=0
m22
Từ đó giải ra ta được
1
q1 = C1 sin(ω1t + β1); q2 = - m12 q
+ C2t + C3 (2.39)
Thế biểu thức q1 vào q2 ta được q1 = C1sin(ω1t + β1)
m22
q2 = - m12
m22
C1sin(ω1t + β1)+ C2t + C3 (2.40)
Như thế khi C2 ≠ 0 tọa độ suy rộng q2 sẽ tăng lên vô hạn khi t tăng. Chú ý rằng trong trường hợp này tọa độ q2 sẽ là tọa độ xyclic. Trạng thái cân bằng của hệ không thể thiết lập được đối với tọa độ xyclic.
Trong trường hợp tổng quát ta có
q1 = p1 + p2 = C1 sin(ω1t + α1) + C2t + C3
q2 = v1p1 + v2p2 = v1C1sin(ω1t + β1)+ v2C2t + v2C3 (2.41)
Thí dụ 3.10 : Cho hệ gồm hai khối lượng m1 và m2 nối với nhau bằng lò xo có độ cứng c như hình 3.9. Hãy tìm biểu thức nghiệm tổng quát và một tích phân đầu của hệ.
Lời giải : Động năng và thế năng của hệ có dạng
x1
x2
c
m1
m2
T = 1 2 1 2
m1x 1 + m2x 2
2 2
2
1 2
П = c(x2 – x1)
Thế các biểu thức động năng và thế năng vào phương trình Lagrange loại II ta được
m1x 2 + cx1 – cx2 = 0 m2x 2 - cx1 + cx2 = 0
Phương trình đặc trưng của hệ
Hình 3.9 Hình thí dụ 3.10
𝐂 − ω2
𝐌 =
c − ω2m1 −c
−c c − ω2m2
= 0
Từ đó suy ra
1
ω2 =
→ m1m2ω4 − c m1 + m2ω2 = 0
2
c(m1 m2 ) ; ω2 = 0
m1m2
Ma trận dạng riêng có dạng
V= 1 1
v v
1 2
Trong đó vi được xác định từ phương trình
𝑖
c - 𝜔2 m1 – cvi = 0 → vi = - m1
m
; v2 = 1
2
Vậy ta có
V = 1 1
−m1m2 1
Các phương trình chuyển động của hệ trong dạng tọa độ chính
1
p 1 + ω2 p1 = 0 p1 = A cos(ω1t + α)
p 2 = 0 p2 = B1 + B2t
Trở lại tọa độ x1, x2 ta có
x1 (t) = p1 (t) + p2 (t) = B1 + B2t + A cos(ω1t + α)
x2 (t) = - m1
m2
p1 (t) + p2 (t) = B1 + B2t -
m1 A cos(ω1t + α) m2
Các hằng số A, α, B1, B2 được xác định từ các điều kiện đầu Gọi xc là tọa độ khối tâm cơ hệ, theo định nghĩa khối tâm ta có
(m1 + m2)xc = m1x1 + m2(1+ x2)
Từ định lý bảo toàn động lượng ta có
(m1 + m2)x c = m1x 1 + m2x 2 = const (2.42)
Biểu thức (2.42) là một tích phân đầu của hệ
c) Trường hợp 3: ω1 ≈ ω2
Phương trình dao động ở dạng tọa độ chính
1
p 1 + ω2 p1 = 0 → p1 (t) = C1 sin(ω1t + α1)
2
p 2 + ω2 p2 = 0 → p2 (t)= C2 sin(ω2t + α1) Trong đó C1, C2, α1, α1 là các hằng số
Trở lại tọa độ q1, q2 theo (2.24) ta có
q1 = p1 + p2 = C1 sin(ω1t + α1) + C2 sin(ω2t + α1) (2.43) q2 = v1p1 + v2p2 = v1C1 sin(ω1t + α1) + v2C2 sin(ω2t + α1) (2.44)
do ω1 ≈ ω2 nên ω2 − ω1 ≪ ω1 . Nếu ta đặt
φ t = ω2 − ω1t + (α2 − α1) (2.45) thì φ (t) thay đổi chậm theo thời gian. Từ (2.43) ta suy ra
q1 = C1 sin(ω1t + α1) + C2 sin(ω2t + α1 +φ)
= C1 sin(ω1t + α1) + C2sin(ω2t + α1) cosφ + sinφ cos (ω2t + α1)
= (C1 + C2 cosφ) sin(ω2t + α1)+C2 sinφ cos (ω2t + α1)
Tính toán tương tự ta được
q2 = (v1C1 + v2C2 cosφ) sin(ω2 t + α1)+ v2C2 sinφ cos (ω2t + α1)
Nếu ta đặt
C1 + C2cosφ = A1 cosθ1; C2sinφ = A1 sinθ1
v1C1 + v2C2 cosφ = A2 cosθ2; v2C2 sinφ = A2 sinθ2 thì các biểu thức q1(t) ; q2(t) có dạng
q1(t) = A1(t) sin(ω1t + α1 + θ1)
q2(t) = A2(t) sin(ω1t + α1 + θ1) (2.46)
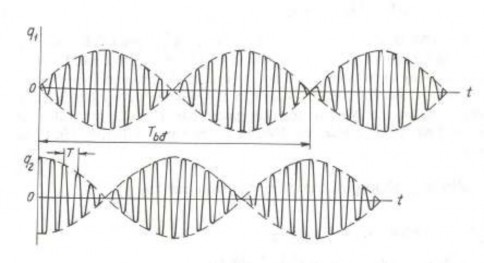
Hình 3.10 Hiện tượng phách trong dao động
Trong đó
A
= C2 + C2 + 2C C
cos φ ; tgθ
C2 sin φ
=
1 1 2 1 2
1 C1 + C2 cos φ
A = v2 C2 + v2 C2 + 2v v C C
cos φ ; tgθ
v2 C2 sin φ
=
1 1 1 2 2
1 2 1 2
1 v1C1 + v2 C2 cos φ
Do góc φ(t) thay đổi chậm theo thời gian nên các hàm A1, A2, θ1;θ2 thay đổi chậm theo thời gian. Từ (2.46) ta thấy chu kỳ thay đổi biên độ
2 π
ω
Tbd =
2
− ω1
rất lớn so với chu kỳ T = 2π ω1. Hiện tượng dao động như thế gọi là hiện tượng phách. Đồ thị dao động có dạng như hình 3.10
Thí dụ 3.11 : Tìm điều kiện xuất hiện hiện tượng phách đối với mô hình dao động trong thí dụ 3.7
Lời giải : Theo thí dụ 3.7 ta có
1
ω2 = g
l
; ω2 = g l
2cd2
+ ml2
2
Hiện tượng phách xuất hiện khi
ω ω = g ω2 ω2 << ω2
2 1 l 2 1 1
Từ các công thức trên suy ra điều kiện xuất hiện hiện tượng phách
2cd2 g 2cd2
ml2 =
l ml2 = g
3.3 DAO ĐỘNG TỰ DO CÓ CẢN
Phương trình vi phân dao động tự do có lực cản tỷ lệ với vận tốc của hệ n bậc tự do có dạng
M 𝐪 + B 𝐪 + C q = 0 (3.1)
Trong đó M, B, C là các ma trận vuông cấp n với các phần từ là các hằng số. Cũng giống như ở hệ một bậc tự do, tùy theo cấu trúc của ma trận cản B, hệ có thể thực hiện dao động tự do tắt dần và cũng có thể thực hiện chuyển động không dao động. Về phương diện dao động, ta quan tâm chủ yếu đến trường hợp hệ thực hiện dao động tự do tắt dần. Như thế bài toán quan trọng hàng đầu trong đoạn này là xác định khi nào hệ thực hiện dao động tự do tắt dần, sau đó mới đến thuật toán tìm nghiệm.
3.3.1 Phương pháp giải trực tiếp (ma trận cản tùy ý)
a) Phương trình xác định giá trị riêng
Ta tìm nghiệm của phương trình (3.1) dưới dạng
q(t) = 𝐪 eλ t , 𝐪 là véc tơ hằng (3.2)