Chọn Kích Thước Mặt Cắt . Nếu Biết Lực Dọc Và Ứng Suất Cho Phép Từ (4.25) Đễ Dàng Suy Ra Diện Tích Mặt Cắt Ngang:

như hình 4.15.

Vì mặt cắt ngang sau biến dạng vẫn phẳng và vuông góc với trục thanh cho nên sau khi biến dạng mặt cắt 1'-1' vẫn song song với mặt cắt 2-2 và mặt cắt 1-1. Vậy tất cả các thớ dọc của đoạn thanh đều có độ dãn dài như nhau là dz và biến dạng dài tương đối z là hằng số đối với tất cả các điểm trên mặt cắt.

dzconst dz

Theo định luật Hooke ta có:

(4.12)

z

z E

(4.13)

trong đó: E là hằng số tỷ lệ, được gọi là mô đun đàn hồi khi chịu nén hoặc chịu kéo, nó phụ thuộc vào vật liệu.

Từ (4.12) và (4.13) ta thấy ứng suất pháp phân bố đều trên toàn bộ mặt cắt

Có thể bạn quan tâm!

• Biểu Thức Động Năng Của Vật Rắn Chuyển Động
• Vật Quay Xung Quanh Một Trục Cố Định Với Vận Tốc 
• Phương Pháp Mặt Cặt Biến Thiên- Các Thành Phần Nội Lực Trên Mặt Cắt Ngang
• Quan Hệ Giữa Nội Lực Và Cường Độ Tải Trọng Phân Bố.
• Ứng Suất Pháp Của Dầm Chịu Uốn Ngang Phẳng
• Điều Kiện Cường Độ- Ba Bài Toán Cơ Bản

Xem toàn bộ 180 trang tài liệu này.

z E.z const

Thay vào (3.1) ta được:

Nz

z F

(4.14)

trong đó F là diện tích mặt cắt ngang.

4.2.3.4. Biến dạng dọc và ngang

1. Biến dạng dọc

Khi thanh chịu kéo hay nén đúng tâm, chiều dài l của thanh thay đổi một lượng l -

l được gọi là biến dạng dọc tuyệt đối. Từ công thức (4.12) ta có:

dz z .dz . (4.15)

Thay (4.14) vào (4.15) ta được:

dz 



l

Nz dz EF

N

(4.16)

Từ (4.16) ta có:

l z dz

0 EF

(4.17)

Trong trường hợp Nz/EF = const trên suốt chiều dài l hoăc

có tri ̣số không đổi

trong từ ng đoan

thanh thì (4.17) có dạng:

l Nz .l

EF

(4.18)

n

l 

N zi li

(4.19)

i 1 Ei Fi

trong đó EF được gọi là độ cứng của thanh khi kéo - nén.

Vậy: biến dạng dọc của một thanh chịu kéo (hoặc nén) đúng tâm tỷ lệ thuận với lực dọc và chiều dài thanh và tỷ lệ nghịch với độ cứng của thanh.

2. Biến dạng ngang

Theo phương ngang thanh cũng có biến dạng. Gọi x và y là biến dạng dài tương đối theo hai phương x và y, Poat- xông đã tìm được mối liên hệ giữa x, y và z như sau:

x = y = -z

trong đó:  là hệ số Poát - xông; nó phụ thuộc vào vật liệu.

Ví dụ: Thép:

 0, 25  0,33 ; Gang:

 0, 23  0, 27 ;

Nhôm:

 0,32  0,36 ; Đồng:

 0,31 0,34 .

Ví dụ 4.2. Một cột có sơ đồ chịu lực như hình vẽ 4.16. Tính ứng suất trong cột

và biến dạng dài tuyệt đối của cột. Biết: E  20.1010 N / m2 ,

P  2000N, P  5000N, P  7000N, F 10cm2 , F

 20cm2.

1 2 3 2 2

P

2000

-

3000

+

4000N

-

P

P

Bài giải

Ta có:

0,5m

1

Nz1 2000 200 N/cm2

F110

2

Nz 2 3000  300

N/cm2

F110

0,8m

3

Nz3 3000  150

N/cm2

0,5m 0,4m

F220

4

Nz 4 4000 200

N /cm2

F220

Để xác định biến dạng dài tuyệt đối của thanh ta sử dụng công thức (4.18) cho bốn đoạn thanh rồi cộng các kết quả lại.

Hình 4.16

l 

2000.0, 5 

3000.0,8 

3000.0, 4 

4000.0, 5

 2.105 m

20.1010.0, 001 20.1010.0, 001 20.1010.0, 002 20.1010.0, 002

Biến dạng dọc mang dấu dương nghĩa là thanh bị giãn dài ra.

Ví dụ 4.3.

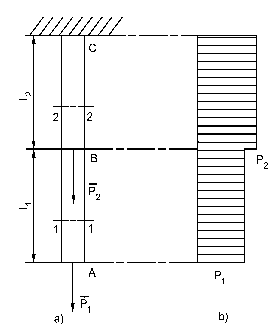
Một thanh thép dài 4m (hình 4.17a) có tiết diện vuông mỗi cạnh a = 20mm chịu hai lực P1 = 80kN ở mút A và P2 = 20kN ở điểm giữa B. Cho biết E = 2.105N/mm2,  = 0,25. Hãy tính chuyển vị của mút thanh và biến dạng tuyệt đối của kích thước ngang tại mặt cắt nguy hiểm.

Bài giải:

1. Lập biểu đồ lực dọc

2. Biến dạng dọc (độ giãn) của thanh:

l l

l

Nz l

Nz l

1N

N 

4,5mm

1 2

1 2 EF EF EF z1 z2

Các mặt cắt nguy hiểm thuộc đoạn BC: ứng suất pháp bằng:

Nz100.103

2250N / mm2

z F 400

Biến dạng dọc (tương đối) của đoạn này bằng:

250

0,00125 0,125%

z E 2.105

Biến dạng ngang: ex = ey = ez = 0,25.0,00125 = 0,03125%

Biến dạng tuyệt đối của mặt cắt ngang (lượng co):

a xa 0,0003125.20 0,00625mm

Biến dạng ngang rất nhỏ so với biến dạng dọc.

4.2.3.5. Đặc trưng cơ học của vật liệu

Hình 4.17

Để nghiên cứu khả năng chịu lực của vật liệu, ta thường tiến hành các thí nghiệm kéo, nén đối với các loại vật liệu khác nhau. Vật liệu được chia làm hai loại: vật liệu dẻo và vật liệu giòn. Vật liệu dẻo là vật liệu bị phá hoại khi biến dạng khá lớn như: thép, đồng, nhôm. v.v... Vật liệu giòn là vật liệu bị phá hoại ngay khi biến dạng còn nhỏ như gang, đá, bê tông.v.v...

0

Mẫu thí nghiệm kéo nén được gia công theo tiêu chuẩn qui định của nhà nước. Mẫu thí nghiệm thường có hình dạng như hình 4.18. Chiều dài thí nghiệm là đoạn có

đường kính

d const . Diện tích mặt cắt ngang ban đầu là

d0

F d2 /4 .

l0

Hình 4.18

P

Pb

P®

PchPtl

1. Kéo vật liệu dẻo

Tương quan giữa biến dạng l và trị số lực kéo P được biểu diễn trên hình 3.9, quá trình chịu kéo của vật liệu được chia thành 3 giai đoạn:

a) Giai đoạn đàn hồi: Tương quan giữa P và l

132 l

Hình 4.19

là bậc nhất. Lực lớn nhất trong giai đoạn này là lực tỷ lệ Ptl. Tương ứng với Ptl ta có gới hạn tỷ lệ:

tl

Ptl Fo

(4.20)

b) Giai đoạn chảy: Lực kéo không tăng nhưng biến dạng tăng liên tục, tương quan giữa biến dạng và lực là đường nằm ngang. Lực tương ứng với giai đoạn này là Pch và ta có giới hạn chảy là:

ch

Pch Fo

(4.21)

c) Giai đoạn củng cố: Tương quan giữa P và l là đường cong. Lực lớn nhất giai đoạn này là PB và ta có giới hạn bền là:

P

B B

Fo

(4.22)

Nếu ta gọi chiều dài của mẫu sau khi đứt là l1 và diện tích chỗ thắt khi đứt là F1 ta có các định nghĩa sau:

Biến dạng dài tỷ đối (tính theo %) là:

Hình 4.20

l1 lo

l

100%

Độ thắt tỷ đối (tính theo phần trăm) là:

Fo F1 100%

Fo

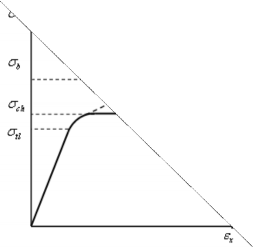
Từ biểu đồ tương quan giữa P và l ta dễ dàng suy ra biểu đồ tương quan giữa biến dạng dài tương đối z = l/ l và ứng suất z = P/Fo như hình 4.20. Khi kể đến sự thay đổi của tiết diện trong quá trình biến dạng thì biểu đồ tương quan giữa ứng suất và biến dạng có đường nét đứt.

2. Nén vật liệu dẻo

Mẫu nén vật liệu dẻo hay vật liệu giòn thường có dạng hình trụ tròn hay hình lập phương (hình 4.21). Khi nén vật liệu dẻo biểu đồ quan hệ giữa biến dạng l và trị số lực P được biểu diễn trên hình 4.21a. Đối với nén vật liệu dẻo ta chỉ xác định

Pch

Ptl

a) l

b) c)

Hình 4.21

được giới hạn tỷ lệ và giới hạn chảy, còn giới hạn bền thì không xác định được do bề ngang

của mẫu phình ra làm diện tích tiết diện liên tục tăng. Mẫu thí nghiệm có dạng hình trống (hình 4.21c).

3. Kéo - nén vật liệu giòn

Biểu đồ kéo – nén vật liệu giòn có dạng đường cong như hình 4.22. Nhưng trong một giới hạn đàn hồi nào đó người ta cũng xem quan hệ giữa lực và biến dạng có dạng bậc nhất.

Đối với vật liệu giòn người ta chỉ xác định được giới hạn bền:

P

B B

Fo

(4.23) P

Đường qui ước

Với vật liệu giòn thì giới hạn bền khi kéo nhỏ hơn rất nhiều so với giới hạn bền khi nén.

Tóm lại, vật liệu dẻo có khả năng chịu kéo và nén như nhau, biến dạng khi phá hỏng các vật

PB B

Ptl A

liệu dẻo lớn hơn vật liệu giòn. Còn vật liệu giòn có khả năng chịu nén lớn hơn khả năng chịu kéo nhiều, biến dạng khi phá hỏng rất nhỏ.

4.2.3.6. Ứng suất cho phép- hệ số an toàn

Ta gọi ứng suất nguy hiểm (ký hiệu o) là trị số ứng suất mà ứng với nó vật liệu bị phá hỏng. Đối

với vật liệu dẻo thì 0 ch đối với vật liệu giòn thì 0 b .

Đường cong thực

l

Hình 4.22

Nhưng trong chế tạo vật liệu thường không đồng chất hoàn toàn, mặt khác trong quá trình sử dụng, tải trọng có thể vượt tải trọng thiết kế, điều kiện làm việc của kết cấu chưa được xem xét đầy đủ, các giả thiết khi tính toán chưa đúng với sự làm việc của kết cấu. Vì vậy ta không bao giờ tính toán các bộ phận theo o. Thường ta chọn

một hệ số an toàn n 1 để xác định trị số ứng suất cho phép:

o

n

4.2.4. Điều kiện cường độ- ba bài toán cơ bản

(4.24)

Như vậy muốn đảm bảo sự an toàn cho các cấu kiện khi thanh chịu kéo-nén đúng tâm thì ứng suất trong thanh phải thoả mãn điều kiện bền:

z Nz / F 

(4.25)

Từ điều kiện cường độ hay còn gọi là điều kiện bền ta có ba bài toán cơ bản:

1. Kiểm tra bền: giả sử biết tải trọng tác dụng lên thanh, biết giá trị của F và []. Trước tiên ta phải xác định nội lực và suy ra ứng suất lớn nhất. Cuối cùng đem so sánh với ứng suất cho phép theo công thức (4.25).

2. Chọn kích thước mặt cắt. Nếu biết lực dọc và ứng suất cho phép từ (4.25) đễ dàng suy ra diện tích mặt cắt ngang:

F Nz / 

(4.26)

3. Xác định tải trọng cho phép: Tương tự, từ (4.25) ta thấy trị số của lực dọc phải thoả mãn điều kiện:

Nz F 

Từ trị số của lực dọc ta có thể tìm được giá trị của tải trọng.

A

B



P

C

Ví dụ 4.4:

Cho kết cấu chịu lực như hình 4.23a. Thanh AB bằng thép, có mặt cắt ngang

(4.27)

hình tròn, đường kính suất cho phép của thép

d 0, 025m . ứng

 140MN / m2 .

NBC

NAB

u

P

Biết  30o . Hãy tính giá trị lớn nhất của

tải trọng P. a)

Bài giải

Dùng mặt cắt 1-1 tách nút B như

hình 4.23b. Chiếu lên phương u vuông góc thanh BC:

NAB sinP cos0

b)

Hình 4.23

(*)

Để tiết kiệm ứng suất trong thanh AB phải bằng ứng suất cho phép []. Lúc đó lực dọc trong thanh phải bằng:

NAB F.

d2

[] 

3,14.0, 0252

140 0, 0686

MN 

4 4

Từ phương trình (*) ta được:

P NAB .tg

P0, 0686.tg30o 0, 0396

MN

Ví dụ 3.3: Cũng bài toán trong Ví dụ trên. Nếu thanh BC làm bằng thép như thanh AB và mặt cắt ngang hình tròn. Hãy chọn đường kính cho thanh BC với giá trị của lực [P].

Giải

Trước tiên ta xác định nội lực trong thanh BC. Từ hình 4.23b ta được:

NBC

sinP 0

hay

NBC

P

sin

[P]

sin

0, 0396 0, 0792 MN

0, 5

Từ điều kiện bền:

NBC z F

4.0, 0792  140 MN / m2

d 2

Từ đó suy ra:

BC BC

dBC 0, 028m

4.3. XOẮ N THUẦ N TÚ Y CỦ A THANH THẲ NG

4.3.1. Khái niệm

Một thanh chịu xoắn thuần tuý là thanh mà trên mọi mặt cắt ngang chỉ có một

thành phần nội lực là mômen xoắn Mz.

Ngoại lực gây ra xoắn là những mômen xoắn tập trung, mômen phân bố nằm trong mặt phẳng vuông góc với trục thanh. (hình 4.24)

Hình 4.24

Trong kỹ thuật, chúng ta thường gặp ngoại lực tác dụng lên các trục thường được cho bởi số vòng quay n (vòng/phút) và công suất N (kW) thì mômen xoắn ngoại lực tác dụng lên trục truyền được quy đổi theo công thức sau:

M  9736. N ,

n

N.m

(4.28)

Nếu công suất được tính bằng mã lực thì mômen xoắn ngoại lực tác dụng lên trục truyền được quy đổi theo công thức sau:

M  7162. N ,

n

N.m

(4.29)

Các chi tiết hay kết cấu chịu xoắn thường gặp như: trục truyền chuyển động, các kết cấu không gian, dây lò xo.v.v…

4.3.2. Nôị lưc

và biểu đồ nôị lưc

Nôi

lưc̣ : Để xác điṇ h mô men xoắn nôi

lưc

trên các măt

cắt ngang của thanh, ta

dùng phương pháp măṭ cắt. Dấu của mô men xoắn nôi

lưc

quy ước như sau:

- Nếu nhìn vào măṭ cắt ta thấy mô men xoắn nôi hồ thì nó có dấu dương (>0).

lưc

quay cùng chiều kim đồng

- Nếu mô men xoắn nôi âm (<0).

lưc

quay ngươc

chiều kim đồng hồ thì nó có dấu

Biểu đồ nội lực: là đường biểu diễn sự biến thiên của mômen xoắn Mz doc trục của thanh. (Vẽ theo phương pháp mặt cắt biến thiên).

Ví dụ 4.5: Vẽ biểu đồ Mz cho thanh chịu lực như hình 4.25.

Bài giải

- Phản lực tại ngàm C:

Mz 0  Mc 900Nm

- Chia dầm thành hai đoạn:

theo

+ Đoạn AB cắt thanh ở mặt cắt z1 (0 z1  40cm)

ta tìm được Mz1 =300 Nm.

và xét sự cân bằng phần trái,

+ Đoạn BC cắt thanh ở mặt cắt z2 và xét sự cân bằng phần phải ta có: Mz2= 900 - 1000.z2

Vẽ biểu đồ Mz như trên hình 4.25.

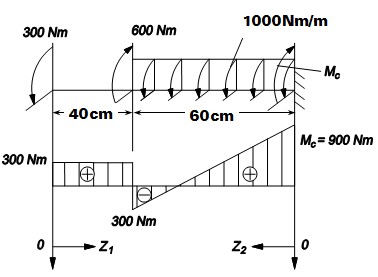
Hình 4.25

4.3.3. Ứng suất trên mặt cắt ngang

4.3.3.1. Ứng suất trên mặt cắt ngang của thanh có mặt cắt tròn

1. Thí nghiệm

Mz

z

z

a) b)

Hình 4.26

Khảo sát một thanh tròn chịu xoắn. Trước khi thí nghiệm ta kẻ ở mặt ngoài các đường thẳng song song với trục và các đường tròn vuông góc với trục. Các đường kẻ này tạo thành một lưới ô chữ nhật như hình 4.26a.

Sau khi chịu xoắn những đường thẳng kẻ song song với trục trở thành những đường xoắn ốc; những đường tròn không bị thay đổi và vẫn vuông góc với trục nhưng lưới ô chữ nhật trở thành lưới ô hình bình hành hình 4.26b.

2. Các giả thuyết tính toán

Từ thí nghiệm trên, ta có thể đưa ra các giả thuyết sau: