Quan Hệ Giữa Nội Lực Và Cường Độ Tải Trọng Phân Bố.

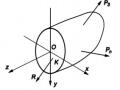
Giả thuyết 1: mặt cắt ngang ban đầu phẳng và thẳng góc với trục của thanh, khoảng cách giữa các mặt cắt là không thay đổi.

Giả thuyết 2: các bán kính của mặt cắt trước và sau thí nghiệm vẫn thẳng và có độ dài không đổi.

3. Công thức ứng suất tiếp



Mx

Trên cơ sở giả thuyết trên, chúng ta có thể xem sự xoắn thanh tròn là kết quả của biến dạng trượt do các

mặt cắt ngang xoay tương đối Mx

đối với nhau quanh trục z. Do

dF

đó, trong các mặt cắt ngang chỉ phát sinh ứng suất tiếp

Có thể bạn quan tâm!

• Vật Quay Xung Quanh Một Trục Cố Định Với Vận Tốc 
• Phương Pháp Mặt Cặt Biến Thiên- Các Thành Phần Nội Lực Trên Mặt Cắt Ngang
• Chọn Kích Thước Mặt Cắt . Nếu Biết Lực Dọc Và Ứng Suất Cho Phép Từ (4.25) Đễ Dàng Suy Ra Diện Tích Mặt Cắt Ngang:
• Ứng Suất Pháp Của Dầm Chịu Uốn Ngang Phẳng
• Điều Kiện Cường Độ- Ba Bài Toán Cơ Bản
• Cơ học ứng dụng - 21

Xem toàn bộ 180 trang tài liệu này.

vuông góc với bán kính. Các Mx ứng suất pháp trên các mặt

cắt ngang và dọc đều bằng không. Vì vậy trạng thái ứng

d

dz

a)

z

b)

Hình 4.27

suất tại mọi điểm của thanh tròn chịu xoắn là trạng thái ứng suất trượt thuần tuý.

Để thiết lập công thức tính ứng suất tiếp, ta tách một đoạn thanh có chiều dài

dz từ một thanh tròn chịu xoắn. Khi chịu xoắn mặt cắt nào đó sẽ bị xoay đi một góc

dso với mặt cắt khác. Góc đó gọi là góc xoắn. Còn góc trượt của thớ nằm cách trục

một khoảng

là 

(hình 4.27a).

Theo định luật Hooke ta có:

G.

(4.30)

trong đó 

là góc trượt tương đối giữa hai điểm nằm trên thớ dọc cách nhau

một khoảng

dz và cách trục thanh một khoảng là .

tg

AB

dz

.d

dz

(a)

Thay (a) vào (5.3) ta có:

G.G.. d

dz

(b)

Lấy một vi phân diện tích dF bao quanh điểm M cách trọng tâm mặt cắt một

khoảng

. Nội lực trên diện tích đó là .dF (hình 5.3b). Từ điều kiện cân bằng tĩnh

học, ta có:

..dF M z F

Thay (b) vào (c) ta có:

(c)

M z 

G d2dF



F dz

(d)

Vì trên một mặt cắt nên tỷ số

dconst dz

do đó công thức (d) được viết lại như sau:

M G. d

z dz

2dF G dJ



p

F dz

(e)

Suy ra:

d

dz

M z

G.J P

(4.31)

Đặt:

dM z

được gọi là góc xoắn tỷ đối.

dz G.JP

Tích số G.JP được gọi là độ cứng chống xoắn của mặt cắt ngang. Thay (4.31) vào (b) ta được:

M z 

JP

(4.32)

trong đó

là khoảng cách từ điểm cần tính ứng

suất đến trọng tâm mặt cắt.

Từ công thức (4.32), ta thấy ứng suất tiếp có quy luật phân bố như hình 4.28 và ứng suất tiếp đạt giá trị max tại những điểm nằm trên chu vi của mặt cắt:

max

M z max

max R

M z R M z

JP WP

(4.33)

Hình 4.28

W JP

P R

 0, 2D3

Wp được gọi là mômen chống xoắn của mặt cắt ngang.

Trong trường hợp tiết diện là hình vành khăn thì:

WP  0, 2D3 (14 )

(4.34)

trong đó:

d

D

4.3.3.2. Biến dạng và chuyển vị của thanh chịu xoắn

Biến dạng của thanh chịu xoắn được thể hiện bằng góc xoắn tương đối giữa các mặt cắt ngang. Từ công thức (4.31) ta có góc xoắn tương đối giữa hai mặt cắt ngang cách nhau một khoảng dz được tính theo công thức:

d

M z dz GJ p

(4.35)

Góc xoắn tương đối giữa hai mặt cắt cách nhau một đoạn l là:



l M

dzdz

0 0 G.JP

trong đó: Mz mômen xoắn là hàm của toạ độ theo trục thanh Mz(z);

(4.36)

J P 

R 4

2

mômen quán tính độc cực của mặt cắt ngang.

G là mô đun đàn hồi khi trượt.

Nếu Mz, G, JP là hằng số trên suốt chiều dài l của thanh thì (4.36) có dạng:

M z .l

G.J P

(rad) (4.37)

Tích số G.JP gọi là độ cứng của thanh chịu xoắn.

Trường hợp thanh có nhiều đoạn và tỷ số

thì công thức (4.36) có dạng:

M z

G.J P

không đổi trong từng đoạn chiều dài li

n



M zi .li

i1 Gi .J iP

(4.38)

Ví dụ 4.6: Cho thanh chịu lực, số liệu và kích thước như hình 4.29a. Vẽ biểu đồ nội lực, tính ứng suất tiếp lớn nhất ở các mặt cắt và góc xoắn tại đầu tự do của thanh. Biết G=8.106 N/cm2.

Bài giải

Biểu đồ nội lực được vẽ như hình 4.29b.

290 Nm

2,8cm

1220 Nm 360 Nm

4 cm

570 Nm

A

B

C

D

0,6 m

0,4 m

0,6 m

a)

290Nm

930Nm

+

-

b)

570Nm

Hình 4.29

Ứng suất tiếp lớn nhất trên các đoạn là:

max(AB)

M z ( AB)

WP( AB)

 29000

0,2.2,83

 6600 N / cm2

Mz(BC) 930007260N / cm2

max(BC)

WP(BC)

0, 2.43

Mz(CD) 570005420N / cm2

max(CD)

Tính góc xoắn:

WP(CD)

0, 2.43

D AB BC CD 

M i .li 29000.60 93000.40 57000.60 3

z 2, 3.10

rad

P

G.J i 8.106.0,1.2,84 8.106.0,1.44 8.106.0,1.44

4.3.4. Điều kiện cường độ– ba bài toán cơ bản

4.3.4.1. Điều kiện cường độ

Để đảm bảo điều kiện bền thì ứng suất tiếp quá giá trị ứng suất cho phép:

max

trong thanh không được vượt

max

M z

W

 []

(4.39)

trong đó:



p

ứng suất tiếp cho phép.

ứng suất cho phép được xác định như sau:

[] 0

n

trong đó

hỏng vật liệu.

0 là ứng suất nguy hiểm được xác định bằng thí nghiệm xoắn phá

Ta cũng có thể sử dụng các thuyết bền để xác định

. Nếu sử dụng thuyết bền

ứng suất tiếp lớn nhất thì



được xác định theo biểu thức sau:



[] 

2

Nếu sử dụng thuyết bền thế năng biến đổi hình dáng thì:



3

[] 

4.3.4.2. Ba bài toán cơ bản

- Kiểm tra bền theo (4.39);

- Chon

điṇ h kích thước mặt cắt ngang: W M z ;

p 

- Xác định tải trọng cho phép tác dụng lên thanh:

M z Wp 

Ví dụ 4.7: Cho một trục tròn chịu xoắn bởi các mômen như hình 4.30. Biết:

MA 100kNcm, MB MC 25kNcm, MD 50kNcm . Hãy xác định đường kính

trục theo điều kiện bền, cho

2kN / cm2 .

Bài giải: Dùng phương pháp mặt cắt, dễ dàng ta vẽ được biểu đồ mômen xoắn như hình 4.30b.

Trên đoạn CD, Mz có giá trị tuyệt đối lớn nhất

Mz 50kNcm .

Để xác định đường kính trục theo điều kiện bền, ta sử dụng công thức (4.39):

max

M z

W

 []

p

M

M

M

M

B

C

A

1m

1m

1m

a) D

50

50

Mz

b)

25

Hình 4.30

16Mz

3 

3 16.50

3,14.2

5, 03cm

16Mz

Hay:

d3

d 

Ta chọn d 5 cm .

Ví dụ 4.8

Cho một trục rỗng chịu lực như hình 4.31a. Các puli 1, 2, 3 là bị động có công suất N1 = 40 mã lực, N2 = 20 mã lực, N3 = 30 mã lực, puli 0 là chủ động.

a)

b)

Hình 4.31

Cho biết n =1000vòng/phút, =d/D =0,6, []=4500N/cm2, G=8.106N/cm2. Xác định D, d.

Bài giải:

Biểu đồ công suất được vẽ trên hình 4.31b. Mặt cắt nguy hiểm có N0 = 50 mã lực

MZ max

 71620 N  716200 50Ncm

n 1000

Chọn kích thước theo điều kiện bền (5-11), ta có:

Mz 

D3 4

716200.N0

Wp 

wP 

(1 ) 

16

n 

3

16 716200.N0

 n (1 )

4

D  3, 64cm

Vậy ta chọn: D=3,64; d=3,64 0,6 = 2,18 (cm).

4.4. UỐN PHẲNG CỦA THANH THẲNG

4.4.1. Khái niệm

Một thanh chịu uốn là thanh có trục bị uốn cong dưới tác dụng của ngoại lực.

Những thanh chủ yếu chịu uốn gọi là dầm.

x

z

Đường tải trọng

y

Mặt phẳng tải trọng

Ngoại lực gây ra uốn là những lực tập trung, lực phân bố có đường tác dụng vuông góc với trục dầm hoặc những

mômen tập trung, mômen phân bố nằm trong mặt phẳng chứa trục dầm.

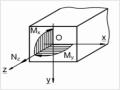
Mặt phẳng tải trọng là mặt phẳng chứa ngoại lực tác dụng (hình 4.32).

Đường tải trọng là giao tuyến của mặt phẳng tải trọng với mặt cắt ngang của dầm.

Mặt phẳng quán tính chính trung tâm là mặt phẳng chứa trục dầm và một trục quán tính chính trung tâm.

Mặt phẳng đối xứng là mặt phẳng

được tạo bởi trục đối xứng và trục dầm.

Nếu trục của dầm sau khi bị uốn

Hình 4.32

là một đường cong nằm trong mặt phẳng quán tính chính trung tâm thì sự uốn đó gọi là uốn phẳng.

Trong kỹ thuật, những dầm chịu uốn thường có mặt cắt ngang có ít nhất một trục đối xứng và mặt phẳng tải trọng trùng với mặt phẳng đối xứng, tức là đường tải trọng trùng với trục đối xứng của mặt cắt ngang. Trong những trường hợp này dầm chịu uốn phẳng.

Uốn phẳng được chia làm hai loại: uốn thuần tuý và uốn ngang phẳng.

- Uốn thuần tuý phẳng: Trên MCN của dầm chỉ có một thành phần mômen uốn Mx (My) nằm trong mặt phẳng quán tính chính trung tâm.

- Uốn ngang phẳng: Trên MCN của nó có hai thành phần nội lực là lực cắt Qy và mômen uốn Mx (hoặc Qx và My).

4.4.2. Nội lực và biểu đồ nội lực

4.4.2.1. Nội lực

Theo mục 4.1.3 các thành phần nội lực Qy và Mx được quy định về chiều như sau:

- Lực cắt Qy được coi là dương nếu pháp tuyến ngoài của mặt cắt ngang quay một góc 900 thuận chiều kim đồng hồ thì gặp chiều của lực cắt Qy.

- Mô men uốn Mx được coi là dương nếu nó làm thớ dưới trục dầm bị kéo tức là làm căng các thớ về phía dương trục y, (trong dầm chọn chiều dương y hướng xuống dưới).

4.4.2.2. Biểu đồ nội lực

1. Quan hệ giữa nội lực và cường độ tải trọng phân bố.

Xét một đoạn thanh giới hạn bởi hai mặt cắt 1-1 và 2-2. Hai mặt cắt cách nhau một khoảng dz chịu tác dụng của tải

trọng phân bố qz, qui ước hướng lên trên là chiều dương.

Qy Mx

N

q(z)

Mx+dMx

Nz+dNz

Mặt cắt 1-1 có

Mặt cắt 2-2 có:

Nz ,Qy , M x .

z

dz

Qy+dQy

Nz dNz ; Qy dQy ; Mx dMx .

Viết phương trình cân bằng cho đoạn thanh khảo sát ta được:

Z Nz dNz Nz  0

Y QyQydQyq z dz  0

dz2

Hình 4.33

M 0 Mx dM x M x Qydz q z. 2

dQz dz

chiều dài.

q( z )

: đạo hàm bậc nhất của lực cắt bằng cường độ của lực phân bố theo

dM x

dz

Qy

: đạo hàm bậc nhất của mômen uốn bằng lực cắt.

dM 2 ( x )

dz2

q( z )

: đạo hàm bậc hai của mômen uốn bằng cường độ lực phân bố theo

chiều dài. Vậy biểu đồ mômen uốn có cực trị tại Qy= 0.

2. Phương pháp vẽ nhanh biểu đồ

* Để vẽ nhanh và kiểm tra biểu đồ nội lực cần:

Dựa trên các nhận xét về bước nhảy:

- Tại mặt cắt có đặt lực tập trung, biểu đồ lực cắt có bước nhảy, trị số bước nhảy bằng trị số lực tập trung.

- Tại mặt cắt có mômen tập trung, biểu đồ mômen uốn có bước nhảy, trị số bước nhảy bằng trị số mômen tập trung.

Dựa trên các liên hệ vi phân giữa ngoại lực và nội lực:

- Trên đoạn thanh không có lực phân bố (q = 0), biểu đồ lực cắt (Qy) là hằng số, mômen uốn (Mx) là đường bậc nhất.

- Lực phân bố q=const - Qy bậc nhất, Mx là đường bậc hai.

- Trên đoạn thanh có q>0 (hướng lên) thì Qy đồng biến, trên đoạn thanh có q<0 (hướng xuống) thì Qy nghịch biến.

- Trên đoạn thanh có Qy>0 thì Mx đồng biến, trên đoạn thanh có Qy<0 thì Mx nghịch biến. Tại mặt cắt Qy = 0, Mx đạt cực trị:

+ Cực đại khi q < 0 (có chiều hướng xuống q ↓)

+ Cực tiểu khi q > 0 (có chiều hướng lên trên q↑)

Dựa trên tính đối xứng và tác dụng của tải trọng:

- Bề lòm của biểu đồ mômen uốn Mx luôn hứng lấy chiều tác dụng của lực phân bố.

- Trường hợp hệ có kết cấu đối xứng chịu tải trọng đối xứng, biểu đồ mômen uốn sẽ đối xứng, biểu đồ lực cắt sẽ phản đối xứng qua trục đối xứng của hệ. Nếu kết cấu đối xứng chịu tải trọng phản đối xứng thì biểu đồ lực cắt đối xứng và biểu đồ mômen uốn phản đối xứng.

Nếu biểu đồ trong đoạn đang xét là hằng số thì chỉ cần một giá trị ở điểm đầu hoặc điểm cuối của đoạn; nếu biểu đồ là đường bậc nhất thì cần hai giá trị ở hai đầu đoạn; nếu biểu đồ là đường cong thì cần ba giá trị tại điểm đầu, điểm cuối và tại nơi có cực trị; nếu không có cực trị thì cần biết chiều lồi lòm của biểu đồ theo dấu đạo hàm bậc hai.

Ví dụ 4.9:

Vẽ biểu đồ mômen uốn M và lực cắt Q của thanh chịu lực như hình vẽ 4.34a theo phương pháp vẽ nhanh.

Bài giải:

Xác định các phản lực liên kết:

MA=0 VB= 4qa

MB=0 VA= - qa

Như vậy VA có chiều hướng xuống.

Ta có các nhận xét và trình tự vẽ biểu đồ như sau:

* Với biểu đồ lực cắt Q:

- Tại mặt cắt A có lực tập trung VA = qa hướng xuống nên biểu đồ lực cắt có bước nhảy xuống. Giá trị bước nhảy bằng qa.

- Trên đoạn AB có lực phân bố đều hướng xuống nên biểu đồ lực cắt là đường bậc nhất xiên xuốcn) g. Lượng biến đổi lực cắt trên đoạn AB bằng hợp lực của lực phân bố trên đoạn đó là 2qa. Như vậy giá trị lực cắt tại mặt cắt bên trái B sẽ là 3qa.

- Tại mặt cắt B có lực tập trung VB = 4qa hướng lên nên biểu đồ lực cắt có bước nhảy lên. Giá trị bước nhảy bằng 4qa. Như vậy giá trị lực cắt tại mặt cắt bên phải B sẽ