Vật Quay Xung Quanh Một Trục Cố Định Với Vận Tốc 

Tbăng =

1 m v2 1 (m ) v2 1 mv2

2 k k 2 k2

Chú ý: vA = vB = v = R.;

IO1

IO2

I Q R2

2g

Động năng của cơ hệ được tính như sau:

Có thể bạn quan tâm!

• Các Đặc Trưng Hình Học Của Cơ Hệ Và Vật Rắn
• Biểu Thức Của Mômen Động Lượng Của Vật Rắn Quay
• Biểu Thức Động Năng Của Vật Rắn Chuyển Động
• Phương Pháp Mặt Cặt Biến Thiên- Các Thành Phần Nội Lực Trên Mặt Cắt Ngang
• Chọn Kích Thước Mặt Cắt . Nếu Biết Lực Dọc Và Ứng Suất Cho Phép Từ (4.25) Đễ Dàng Suy Ra Diện Tích Mặt Cắt Ngang:
• Quan Hệ Giữa Nội Lực Và Cường Độ Tải Trọng Phân Bố.

Xem toàn bộ 180 trang tài liệu này.

T T T

T T T

 1 Q

R22 1 Q R22 1 P1 v2 1 P2 v2 1 mv2 

O1 O2

A B bang

2 2g

2 2g

2 g A 2 g B 2



1 Q P1 P2 2



2 g

mv



Bây giờ ta chuyển sang tính công của các lực. Vì các lực sinh công chỉ gồm các trọng lực và ngẫu lực hằng nên có thể tính công hữu hạn:

A  ( P P )s M ( P P M )s

2 1 2 1 R

Áp dụng định lý động năng dạng hữu hạn ta nhận được:



1 Q P1 P2 2 M



2 g

Vậy: v 

mv

2g

(P2P1)R M

R(Q P1 P2 mg)

s



 ( P2 P1 R )s

3.3.4. Định lý bảo toàn cơ năng

3.3.4.1. Trường lực

Trường lực là khoảng không gian vật lý mà khi chất điểm chuyển động trong trường lực chịu tác dụng của lực chỉ phụ thuộc vào vị trí của nó. Trường trọng lực, trường các lực đàn hồi là những Ví dụ về trường lực.

Trường lực thế là trường lực mà công của lực tác dụng lên chất điểm không phụ thuộc vào dạng quỹ đạo điểm đặt của lực mà chỉ phụ thuộc vào vị trí đầu và vị trí cuối của nó. Lực do trường lực thế tác dụng lên chất điểm đặt trong nó được gọi là lực thế. Trường trọng lực, trường lực đàn hồi tuyến tính là trường lực thế; còn trọng lực, lực đàn hồi tuyến tính là những lực thế.

3.3.4.2. Thế năng

Khảo sát cơ hệ gồm các chất điểm M1, M2, …, MN nằm trong trường lực thế

dưới tác dụng của các lực có thế:

F1, F2 ,..., FN .

Ta quy ước M là tượng trưng cho vị trí của cơ hệ, ví dụ M1 là vị trí của cơ hệ

khi các chất điểm có các vị trí: M (1) , M (1) ,...,M (1) ;

1 2 N

M = Ak(MM0) (3.88)

Vì vị trí “0” được chọn tuỳ ý nên thế năng của cơ hệ tại một vị trí nào đó sai khác hằng số cộng tuỳ ý.

0

Rò ràng thế năng của cơ hệ tại vị trí “0” bằng không, tức là: M = 0

Vì lực thế chỉ phụ thuộc vào vị trí các chất điểm của cơ hệ, nên biểu thức công của nó cũng chỉ phụ thuộc vào vị trí các chất điểm của cơ hệ và do đó thế năng của cơ hệ cũng chỉ phụ thuộc vào vị trí các chất điểm cơ hệ, tức là:

 = (x1, y1, z1, x2, y2, z2,…, xN, yN, zN)

z M1 MN

M

0

F

1

M2

F

N

0

M

N

1

0

F2

M

2

O

y

x

Hình 3.21

Áp dụng công thức tính công ta được:

Thế năng của các trọng lực:

P1, P2 ,...,PN

 = P.h (3.89)

Trong đó (Hình 3.22): P = Pk;

h: là cao độ khối tâm của cơ hệ so với vị trí “0” được chọn, lấy dấu + trong trường hợp khối tâm cơ hệ nằm trên vị trí “0” và lấy dấu – trong trường hợp ngược lại.

z

M1 C

M

0

M

0 k

1

Pk

P1

O

x

Mk MN

C 0

0

MN

P

N

y

O1 O



z

Hình 3.23

Hình 3.22

Thế năng của lực đàn hồi tuyến tính: trường hợp lò xo

1c(z 

20

)2 2 

(3.90)

0

Trong đó: 0 là độ biến dạng của lò xo tại vị trí cân bằng tĩnh 0 so với trạng thái

không biến dạng O1 của lò xo. (Hình 3.23).

3.3.4.4. Định lý bảo toàn cơ năng

Giả sử hệ chuyển động trong trường lực thế từ vị trí đầu M0 đến vị trí M nào đó. Theo định lý động năng ta có:

TM TM 0

AM 0 M

Mặt khác theo tính chất thứ nhất của các lực thế, ta có:

Vậy: Hay:

AM 0 M

TM TM 0

TM M

0 

M M

M M

0 

M M

T 0 0

const

(3.91)

Đại lượng: E = T +  được gọi là cơ năng của cơ hệ, nó bằng tổng của động năng và thế năng của cơ hệ.

Vậy ta có định lý bảo toàn cơ năng:

Khi cơ hệ chuyển động trong trường lực thế thì cơ năng của cơ hệ được bảo toàn.

Hệ cơ học nghiệm đúng định luật bảo toàn cơ năng được gọi là hệ bảo toàn, còn lực tác dụng lên cơ hệ được gọi là lực bảo toàn. Như vậy lực thế là lực bảo toàn.

Nếu ngoài các lực bảo toàn còn có những lực không bảo toàn, chẳng hạn như lực ma sát, tác dụng lên cơ hệ thì cơ năng của cơ hệ sẽ biến đổi do có sự chuyển hoá giữa cơ năng của cơ hệ khảo sát với các dạng năng lượng khác. Cơ hệ như vậy được gọi là hệ không bảo toàn.

Hệ thức (3.91) còn được gọi là tích phân năng lượng.



0

C

P

Ví dụ 3.7. Một vật quay quanh trục nằm ngang O từ vị trí đầu được xác định nhờ góc 0 với vận tốc góc đầu 0. Tìm vận tốc góc của vật quay theo góc quay  của nó. Bỏ qua sức cản của không khí và ma sát tại ổ trục quay.

Khảo sát cơ hệ là con lắc vật lý (Hình 3.24)

Lực tác dụng: gồm phản lực trục quay O, không sinh công và trọng lực P là lực có thế.

Do đó ta có cơ hệ bảo toàn.

Áp dụng định lý bảo toàn cơ năng: E = T +  = const, ta có:

1 I2 Pl cos1 I2 Pl cos

Hình 3.24

2 2 0 0

Vậy:

2 2 2Pl (cos cos)

0 J0

3.4. ĐỘNG LỰC HỌC VẬT RẮN

Việc áp dụng trực tiếp phương trình cân bằng tĩnh học chỉ thuận tiện đối với cơ hệ gồm chỉ một số hữu hạn các chất điểm. Đối với trường hợp vật rắn cần tìm dạng thu gọn của hệ lực quán tính của vật rắn. Dưới đây sẽ trình bày kết quả thu gọn hệ lực quán tính của một số chuyển động thường gặp.

Đầu tiên ta chứng minh rằng đối với vật rắn có chuyển động bất kỳ, véc tơ

chính của hệ lực quán tính của nó luôn luôn bằng:

M

aC

Rqt' 

(3.92)

Trong đó: M là khối lượng của vật;

aC

là gia tốc khối tâm của vật.

Thực vậy, dựa vào định nghĩa của véc tơ chính của hệ lực và định nghĩa của khối tâm vật rắn, ta có:

k

mk ak MaC

Rqt' F qt 

Mômen chính của hệ lực quán tính của vật rắn chuyển động phụ thuộc vào dạng chuyển động cụ thể của vật rắn.

3.4.1. Vật rắn chuyển động tịnh tiến

F2=-mk aC

a

C

rk

Rqt

C

aC

Mômen chính của hệ lực quán tính đối với khối tâm

qt

vật rắn được tính như sau:

Mk(mk)

qt qt

qt 

mCmC(Fk) rkFkrkmkak

rk





Trong đó là véc tơ định vị của chất điểm Mk đối

với khối tâm C, tức

Chú ý rằng:

rk CMk ;

rC  0

(Hình 3.25).



qt 

Hình 4.3

Hình 3.25

akaC;mkrkMrC 0; Fk

Vậy:

mk ak maC

qt





mCrkmkak

akmkrk

aCmkrk

aCmkrk

aC MrC

Do đó thu gọn hệ lực quán tính của vật chuyển động

tịnh tiến về khối tâm C ta được một lực đặt tại khối tâm C. z

Rqt

B

M



aC

(3.93) 

a

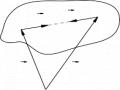
3.4.2. Vật quay xung quanh một trục cố định với vận tốc 

t

a

v

n

góc gia tốc góc K

K k

Chọn hệ trục tọa độ 0xyz gắn liền vào vật quay, trong Mk

đó 0z trùng với trục quay của vật (Hình 3.26). Lấy phần từ Mk’



qt

F

K

qtn

F

K

rk

có khối lượng mk và véc tơ định vị rk

(xk, yk, zk). Gia tốc của

O

117 A

Hình 4.5

chất điểm Nk bằng.

t n 

ak ak ak rk vk ;vk rk

Lực quán tính của chất điểm Mk sẽ là:

F qt m (m (

k k rk ) k vk )

Vậy mômen chính của hệ lực quán tính của vật rắn đối với gốc tọa độ O sẽ bằng:

qt

qt 



k

định theo cá

mo mo (Fk ) rk mk (rk ) rk mk (v )

Trong hệ trục tọa độ đã chọn, các véc tơ được xác

Hình 3.26

c véc

rk , n,



tơ đơn vị

i , j, k trên các trục tọa độ như sau:





rk xk i yk j zk k ;.k ;.k

Sau khi thực hiện các phép tính với chú ý rằng:



i j k; j k;k i j;i i j j k k  0

Ta được:

qt

mo

 (2



2

J yz Jzx )i  (



Jxz Jzy ) j Jzk

(3.94)

Trong đó:

I m y z ; I

m x z ; I

m (x2 y2 )

yz k k k xz

k k k z

k k k

rC

Véc tơ chính của hệ lực quán tính, như trên đã nêu, bằng:

M

aC

Rqt' 

M 

 ( )

rC



Sau khi thay: Chúng ta có:

rC xC i yC j zC k



Rqt M (x 2 y )i M ( y 2 x )J

(3.95)

C C C C

Như vậy thu gọn hệ thức quán tính của vật quay quanh một trục cố định về một điểm nằm trên trục quay của vật ta được một lực tính theo công thức (3.98) và một

ngẫu lực được tính theo công thức (3.95).

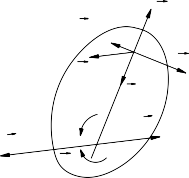
3.4.3. Vật rắn là tấm phẳng chuyển động song phẳng

,

ak

Lấy một chất điểm Mk, khối lượng mk có gia tốc 

ta có: (Hình 3.27)

t

a

MkC

F

qtc

K

qtn

F

K

F

Mk

qt2

K

an

n t

MkC

a

C

C

ak aC aM C aM C

R

qt'

k k

m

C

Trong đó: qt

C

an r 2 ; at r CM k

Hình 4.4

Hình 3.27

M k C k s M k C k s ; rk

Do đó :

F qt F qtc F qtn F qtt

k k k k



k

k

F qtc qtn

n qtt t

Trong đó:

k mmaC ; Fk

mk aM C ; Fk mk aM C

Vậy:

m qt m

(F qtc ) m

(F qtn ) m

(F qtt )

C C k C k C k

Chú ý rằng:

qtc





mC (Fk ) rk mk aC aC mk rk aC MrC  0

qtn

qtn

mC (Fk

)  0

vì các lực Fk

đi qua tâm lấy mômen C.

C

qtt

2 

mC (Fk

) mk rk s Jz s

Trong đó

IzC

m r 2

là mômen quán tính của tấm đối với trục thẳng góc với

k k

mặt phẳng tấm và qua khối tâm C.

Vậy:

m qt I 

C

z

s

C

Kết quả thu gọn hệ lực quán tính của tấm về khối tâm C sẽ là:

C

M

aC

Rqt 

qt 

(3.96)

C

mC I z s

Kết quả này còn đúng cho trường hợp vật rắn chuyển động song song với mặt phẳng đối xứng động lực của nó.

CÂU HỎI ÔN TẬP

1. Trình bày lực quán tính của chất điểm.

2. Trình bày nguyên lý Đalămbe đối với chất điểm, cơ hệ.

3. Trình bày phương pháp Tĩnh hình học- động lực.

4. Một vật nặng M có trọng lượng P = 10N treo vào đầu một sợi dây dài 30cm, đầu kia của sợi dây buộc vào điểm O cố định. Khi chuyển động của vật M vạch thành đường tròn trong mặt phẳng nằm ngang (M chuyển động tròn đều), lúc đó sợi dây hợp với đường thẳng đứng một góc 600.

Xác định vận tốc của vật nặng và sức căng của sợi dây.

5. Một thanh AB đồng chất được gắn bản lề vào một trục

v

O

H

M

Hình 3.28

quay thẳng đứng (Hình 3.29). Cho biết OA = a, OB = b. Trục quay đều với vận tốc góc

, chốt bản lề nằm ngang. Bỏ qua ma sát.

Tìm hệ thức giữa góc nghiêng  giữa trục quay và thanh AB và vận tốc góc 

khi chuyển động quay bình ổn, góc  là hằng số.

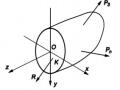
6. Một tấm hình chữ nhật đồng chất trọng lượng P quay đều quanh trục thẳng đứng với vận tốc góc  không đổi.

Hãy xác định lực xé tấm theo hướng vuông góc với trục quay trên tiết diện đi qua trục quay (Hình 3.30).

D

C1

P1



C2

P2

C

z

D

a

a

A z

B b

Hình 3.29

Hình 3.30

Phần 2: CƠ HỌC VẬT RẮN BIẾN DẠNG

Chương 4

CƠ HỌC VẬT RẮN BIẾN DẠNG

4.1. MỞ ĐẦU

Cơ học vật rắn biến dạng- Sức bền vật liệu là môn khoa học nghiên cứu sự chịu lực của vật liệu để đề ra phương pháp tính toán độ bền, độ cứng và độ ổn định của các công trình hay chi tiết dưới tác dụng của ngoại lực.

Yêu cầu về độ bền là vật liệu không bị phá vỡ, nứt.v.v… trong quá trình chịu lực.

Yêu cầu về độ cứng là biến dạng của các cấu kiện hay chi tiết trong quá trình chịu lực không lớn đến mức độ làm ảnh hưởng đến sự hoạt động bình thường của các cấu kiện hay chi tiết đó.

Yêu cầu về độ ổn định là các bộ phận của công trình hay chi tiết dưới tác dụng của ngoại lực vẫn giữ được hình dáng ban đầu.

Khi nghiên cứu tính toán trong Cơ học vật rắn biến dạng ta thường gặp ba dạng bài toán cơ bản sau:

Bài toán 1: Kiểm tra bền của chi tiết hay cấu kiện trong những trường hợp chịu lực khác nhau.

Bài toán 2: Xác định kích thước và hình dáng hợp lý của chi tiết và cấu kiện.

Bài toán 3: Xác định tải trọng cho phép có thể tác dụng lên chi tiết hay cấu kiện.

Đối tượng nghiên cứu của Sức bền vật liệu là a) vật rắn thực, tức là vật rắn khi chịu lực thì bị biến dạng. Ví dụ như thép, đồng, gang, gạch, đá… Đây

là điều khác biệt giữa đối tượng nghiên cứu của Cơ học vật rắn tuyệt đối và Cơ học vật rắn biến dạng

4.1.1. Các khái niệm về thanh

Các chi tiết công trình được phân loại theo tương quan kích thước hình học trong không gian: hình khối, hình tấm hoặc vỏ, hình thanh. b)

Khối: là những vật thể có kích thước theo ba phương tương đương nhau (hình 4.1a).

Tấm và vỏ: là những vật thể có kích thước theo hai phương rất lớn so với phương thứ ba

(hình 4.1b).

Thanh: là những vật thể có kích thước theo c) một phương rất lớn so với kích thước hai phương kia

Hình 4.1

Xem tất cả 180 trang.