Biểu Thức Động Năng Của Vật Rắn Chuyển Động

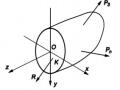
mômen động lượng của vật rắn đối với trục quay là

Lz Iz , trong đó I z

là đại lượng

không biến đổi theo thời gian, nên khi áp dụng công thức (3.61) ta được:

d(I dt

z ) I z

dI dt z

mz (Fk)

Có thể bạn quan tâm!

• Định Luật 2 (Định Luật Cơ Bản Của Động Lực Học)
• Các Đặc Trưng Hình Học Của Cơ Hệ Và Vật Rắn
• Biểu Thức Của Mômen Động Lượng Của Vật Rắn Quay
• Vật Quay Xung Quanh Một Trục Cố Định Với Vận Tốc 
• Phương Pháp Mặt Cặt Biến Thiên- Các Thành Phần Nội Lực Trên Mặt Cắt Ngang
• Chọn Kích Thước Mặt Cắt . Nếu Biết Lực Dọc Và Ứng Suất Cho Phép Từ (4.25) Đễ Dàng Suy Ra Diện Tích Mặt Cắt Ngang:

Xem toàn bộ 180 trang tài liệu này.

(3.65)

Phương trình (3.65) được gọi là phương trình vi phân chuyển động của vật quay quanh một trục cố định, nó còn có thể viết dưới dạng:

I zmz(Fk)

(3.66)

Ví dụ 3.5. Một dây treo vật nặng có trọng lượng Q quấn trên một tang tời có trọng lượng P và bán kính r. Bỏ qua khối lượng dây và ma sát tại ổ trục của tời. Hãy xác định gia tốc góc của tang tời khi vật nặng rơi xuống theo phương thẳng đứng. Cho biết bán kính quán tính của tang tời đối với trục quay của nó là . (Hình 3.15)

Bài giải R

Khảo sát cơ hệ chuyển động của gồm tang tời và vật nặng.

Các ngoại lực tác dụng lên cơ hệ gồm các lực

tời, vật nặng và phản lực R tại ổ đỡ.

Áp dụng (2.45) ta có:

P,Q

của tang O

P

d Lz

m (P) m (Q) mz (R)

dt z z

Biểu thức mômen quán tính của cơ hệ được tính theo công

thức:

tan g v

Q 2 P2 Qr2 Q

Từ đó:

Lz Lz

Lz

I z g r g 

Hình 3.15

dg dt

Qr

P2 Qr 2

Dấu – chứng tỏ tang quay nhanh dần đều theo chiều kim đồng hồ.

3.3.3. Định lý động năng

3.3.3.1. Động năng

Động năng của chất điểm có khối lượng m, chuyển động với vận tốc v là đại lượng vô hướng, được ký hiệu là T:

T 1 mv2

2

(3.67)

Động năng của cơ hệ là tổng động năng của các chất điểm thuộc cơ hệ



v

T 1 m 2

2 k k

(3.68)

Đơn vị của động năng là kgm2 / s2 .

3.3.3.2. Công và công suất

1. Công nguyên tố của lực

Công nguyên tố của lực F , điểm đặt của nó chuyển động theo đường cong C, sau khoảng thời gian dt thực hiện di chuyển nguyên tố ds được xác định theo công thức sau:

d ' A Ft ds

(3.69)

Trong đó Ft

là hình chiếu của lực lên phương tiếp tuyến của quỹ đạo tại điểm

đặt của lực F (Hình 3.16).

M

M1

v



M2

C

r

F

O

y

Hình 3.16

z

x

Công nguyên tố của lực

d' A

có thể dương, âm hoặc bằng không tùy thuộc góc

giữa lực F và vận tốc góc v của điểm đặt lực F là nhọn, tù hoặc góc vuông.

Công nguyên tố của lực còn được viết trong các dạng sau:

d' A F cos.ds F.d r F.v.dt Ft vt dt Fxdx Fy dy Fz dz

Trong đó:

là góc giữa lực F và vận tốc góc v ;

r là véc tơ định vị của điểm đặt lực;

(3.70)

Ft , vt là hình chiếu lên phương tiếp tuyến của quỹ đạo tại điểm đặt của lực F ;

Fx , Fy , Fz là các hình chiếu của lực F lên các trục tọa độ Đề các Oxyz .

Trong trường hợp chất điểm chịu tác dụng của nhiều lực thì F là hợp lực của các lực đó.

2. Công hữu hạn của lực

Khi điểm đặt lực F di chuyển từ vị trí M1 đến vị trí M2 công cả lực F ứng với di chuyển đó được xác định như sau:

s2 r2 t2 

M M

A 1 2 F cos.ds Fdr F.v.dt Fx dx Fy dy Fz dz

s1 r1 t1

M1M 2

Khi chất điểm chịu tác dụng của nhiều lực thì lực F là hợp lực của các lực đó

và rò ràng ta có tính chất sau:

Công (công nguyên tố) của hợp lực bằng tổng công (tổng công nguyên tố) của các lực thành phần.

Đơn vị của công là Nm còn được gọi là Jun (J).

3. Công suất



Công suất là công do lực sinh ra trong một đơn vị thời gian. Công suất được ký hiệu là W.

W d ' A

dt

F.dr 

 .



F v

dt

(3.71)

Biểu thức của công suất có thể viết trong các dạng sau:

W Fcos.v Ft .vt Fx xFy yFz z

Đơn vị của công suất là Oát (w) 1w= 1 J/s

3.3.3.3. Định lý động năng

Định lý. Đạo hàm theo thời gian động năng của chất điểm bằng công suất của lực tác dụng lên chất điểm:

dT 

dt



F.v

(3.72)

Chứng minh: Viết phương trình cơ bản của động lực học cho chất điểm, sau đó nhân vô hướng hai vế với vận tốc của chất điểm, ta có:



m.a.v F.v

Chú ý rằng:

m. 



a.v

ta có ngay:

d (1

dt 2

mv2 ) 

d (1

dt 2

mv2 ) dT

dt

dT 

dt



F.v

Đó là điều cần chứng minh.

v.

r

Phương trình (3.72) còn có thể viết như sau:

dT 

Vậy ta có:

F.dt

F.dd ' A

(3.73)

Định lý: Vi phân động năng của chất điểm bằng công nguyên tố của lực tác dụng lên chất điểm.

Định lý: Đạo hàm theo thời gian động năng của cơ hệ bằng tổng công suất của các nội lực và ngoại lực tác dụng lên cơ hệ:

dT F e .v F i .v

(3.76)

dt k k k k

Chứng minh. Đối với chất điểm Mk thuộc cơ hệ, có khối lượng mk, chịu tác

F

k

dụng của ngoại lực e

và nội lực

k

Fi , theo (3.72), ta có:

d 1 2 e i e i

(

dt 2

mk vk )  ( Fk

Fk ).vk Fk .vk Fk .vk

Khi lấy tổng theo hai vế của đẳng thức vừa nhận được, ta có:

d 1 2 d 1

2 dT e i

dt ( 2

mk vk ) 

dt 2

(mkvk) 

dt Fk .vk Fk .vk

Đó là điều cần chứng minh.

Tương tự với trường hợp của chất điểm ta có:

Định lý: Vi phân động năng của cơ hệ bằng tổng công nguyên tố của các ngoại lực và nội lực tác dụng lên cơ hệ.

k

k

dT F e.dr

F i .d

(3.75)

k

k

Chứng minh: Từ công thức (3.74) ta nhận được:

k

k

k

k

k

k

k

k

dT F e.v dt F i .v dt F e.dr F i .d

Đó là điều cần chứng minh.

Các định lý trên cho biết tốc độ biến đổi của động năng theo thời gian. Dưới đây sẽ trình bày các định lý về biến đổi của động năng trong khoảng thời gian hữu hạn (lượng tích tụ của động năng).

Định lý: Biến thiên động năng của chất điểm trong một chuyển dời nào đó bằng công của lực tác dụng lên chất điểm sinh ra trong chuyển dời đó.

1 1

2 2 2

r2 



1 

mv2 

mv2 F.dr

r1

(3.76)

Chứng minh. Tích phân hai vế của đẳng thức (3.73) với các cận tương ứng ta nhận ngay được công thức (3.76)

Định lý: Biến thiên động năng của cơ hệ trong một khoảng thời gian nào đó bằng tổng công các ngoại lực và nội lực sinh ra trong chuyển dời ứng với khoảng thời gian đó.

T T F e.dr Fi .d

(3.77)

2 1 k k k k

Chứng minh. Định lý sẽ được chứng minh, khi ta lấy tích phân hai vế của đẳng thức (3.75) theo các cận tương ứng:

dT 

F e.dr Fi .d

Từ đó:



T T

k k 

F e.dr 

k k

Fi .d

2 1 k k k k

Đó là điều cần chứng minh.

Cần chú ý rằng nội lực làm biến đổi động năng của cơ hệ. Vì vậy định lý động

năng phản ánh bản chất quá trình thay đổi chuyển động của cơ hệ và nhờ nó trạng thái chuyển động của cơ hệ được nghiên cứu một cách sâu sắc.

3.3.3.4. Áp dụng

1. Biểu thức động năng của vật rắn chuyển động

a) Vật rắn chuyển động tịnh tiến: Vật có khối lượng M chuyển động với vận tốc v . Trong trường hợp này các phần tử của vật đều có cùng vận tốc v, do đó:

T 1m v21m v21m v21Mv2

(3.78)

2 k k 2 k 2 k2

b) Vật rắn quay quanh một trục cố định: Xét một phần tử Mk của vật rắn, có khối lượng mk, nằm cách trục quay một đoạn rk. Vận tốc của Mk sẽ bằng vk = rk, trong đó  là vận tốc góc của vật quay quanh trục cố định. Do đó:

T 1m v2 1m (r )2 1m r 2 2 1I 2

(3.79)

2 k k 2 k k 2 k k 2 z

Trong đó Jz là mômen quán tính của vật đối với trục quay.

c) Vật rắn chuyển động song phẳng: Trường hợp của tấm phẳng có vận tốc khối

tâm C là

vC , có vận tốc góc đối với khối tâm C là s và có khối lượng M.

T 1 Mv2 1 I 2

2 C 2C

Trong đó IC là mômen quán tính của tấm đối với trục qua khối tâm C và thẳng góc với mặt phẳng tấm.

2. Biểu thức công của một số lực

a) Công của trọng lực. Giả sử chất điểm M chịu tác dụng của trọng lực P , di chuyển theo một đường cong C nào đó (Hình 3.17). Để tính công trọng lực ta sử dụng công thức:

M M

A 1 2 Fxdx Fy dy Fz dz

M1M 2

Khi chọn trục Oz hướng thẳng đứng lên thì: Px = Py = 0; Pz = - P

Vậy:

z

M2(x2,y2,z2)

(C) P'

M1(x1,y1,z1)

O P

y

x110

Hình 3.17

1 2 2 1

z2

AM M Pdz P(z z ) P.h

z1

Trong đó h là độ cao di chuyển.

(3.80)

Công của trong lực sẽ dương khi điểm đặt của lực hạ xuống và âm khi điểm đặt của lực được nâng lên và bằng không khi điểm đặt của lực di chuyển trong mặt phẳng ngang.

Công của trọng lực không phụ thuộc vào dạng của quỹ đạo của điểm đặt lực mà chỉ phụ thuộc vào vị trí đầu và vị trí cuối của điểm đặt. Khi điểm đặt di chuyển được một đoạn đường khép kín thì công của lực bằng không.

Công của hệ các trọng lực. Khi cơ hệ di chuyển tù vị trí I đến vị trí II, các chất

k

điểm của nó di chuyển tương ứng từ vị trí chuyển từ CI đến CII.

( I )

M

k

đến

M ( II ) , còn khối tâm cơ hệ di

Công của các trong lực trong di chuyển đó sẽ bằng:

k

k

k

k

k

k

k

CII

CI

A P ( z( II ) z( I ) ) P z( II ) P z( I ) P(z z

C

) Ph

(3.81)

Trong đó: P = Pk;

và I của cơ hệ;

z và

C

II

z : là cao độ của khối tâm của cơ hệ ứng với các vị trí II

C

I

hC: là cao độ của di chuyển khối tâm.

c

r

b) Công của lực đàn hồi tuyến tính

Lực đàn hồi tuân theo định luật Húc:

F 

Trong đó: r là véc tơ định vị của chất điểm so với tâm, còn c là hệ số tỷ lệ không đổi, được gọi là hệ số cứng (Hình 3.18)

M1

M

r1

r

r2

M2

O

y

z

x

Hình 3.18

Công của lực F khi điểm đặt của nó di chuyển từ M1 đến M2 được tính theo công thức:



r2 



r2 



1 r2 

1 r2

2

A Fdr crdr cd (r )2

cd (r)2



r1 r1 r1

2 r1

Vậy:

A c (r2 r2 )

(3.82)

2 2 1

Trong trường hợp lò xo, công của lực đàn hồi lò xo khi đầu mút của nó bị biến dạng một đoạn  so với trạng thái không biến dạng (trạng thái tự nhiên) của nó bằng:

A c 2

2

Cũng như trường hợp của trọng lực, công của lực đàn hồi tuyến tính không phụ thuộc vào dạng quỹ đạo của điểm đặt lực mà chỉ phụ thuộc vào vị trí đầu và cuối của nó.

c) Công của lực tác dụng lên vật rắn chuyển động tịnh tiến

Theo công thức tính công nguyên tố, ta có:

d ' A 

F.dr F.v.dt F.vC .dt F.drC

d) Công của lực tác dụng lên vật quay quanh một trục cố định:

Sử dụng công thức:

d ' A Ft .vt .dt Ft .R..dt mz (F )d

(3.83)

Công của ngẫu lực tác dụng lên vật quay quanh một trục cố định, ngẫu lực có mômen m và nằm trong mặt phẳng thẳng góc với trục quay:

d ' A md

e) Công của lực đặt vào tấm chuyển động song phẳng

(3.84)

Xem tấm song phẳng quay quanh một trục thẳng góc với mặt phẳng của tấm và đi qua tâm quay tức thời. Áp dụng trực tiếp công thức tính công của lực tác dụng vào vật quay ta có:

d ' A mP (F )ds

(3.85)

Trong đó:

mP (F)

là mômen của lực F đối với tâm quay tức thời.

Công thức (3.85) có thể được viết trong dạng:

d ' A mC

(F )ds



F d



C rC

(3.86)

Trường hợp tấm phẳng chịu tác dụng ngẫu lực nằm trong mặt phẳng tấm và có mômen m thì:

d ' A mds

g) Công của hệ nội lực trong vật rắn

(3.87)

F

Xét hai phần tử bất kỳ của vật rắn Mk và M’k. Lực tác dụng tương hỗ giữa hai

k

phần tử đó ký hiệu là MkM’k.

Fk và

' với

Fk F'k

. Hai lực này đều có cùng phương với

Theo công thức tính công nguyên tố ta có:



dA 

, 

,

, '

k Fk drk F 'k drk

Fk drk Fk drk

Fk d (rk rk ) Fk d (M k M k )

k

k

Vì lực Fk cùng phương và ngược chiều với M ' M



nên:

k

k

Fk k

M ' M

Trong đó: k là đại lượng vô hướng dương nào đó. Vậy:



dA '

k Fk d (M k M k )

k

(M ' M

k

k

)d (M ' M )

k

k

k d (M ' M )2

F F'

M'k

2 k k

Mk k k

k d (M ' M )2

2 k k

 0

rk r'

Vì theo định nghĩa vật rắn, khoảng cách giữa k

hai điểm M’k và Mk luôn luôn không đổi.O

Từ đó: dA = dAk = 0

tức: tổng công các nội lực của vật rắn luôn luôn bằng không.

Hình 3.19

Ví dụ 3.6. Một hệ thống chuyền tải gồm hai trục là các trục đặc tròn đồng chất có trọng lượng Q, bán kính R quay quanh các trục quay riêng

cố định O1 và O2 và băng tải là đoạn dây khép kín không giãn,

có khối lượng m. (Hình 3.20). O2

Các gầu xúc có trọng lượng P1 và P2. Trục quay O1 chịu tác dụng ngẫu lực M = const. Tìm vận tốc của gầu xúc theo

đoạn đường di chuyển, cho biết ban đầu hệ đứng yên. B

Bài giải P2

Khảo sát cơ hệ gồm: Hai trục quay, băng tải, hai gầu A

xúc A và B. P1

Lực tác dụng lên cơ hệ: lực sinh công gồm các trọng

lực: P1 ; P2 và ngẫu lực M (các trọng lực của hai trục quay và O1

băng tải không sinh công vì điểm đặt của chúng đứng yên). M

Đầu tiên ta tính biểu thức động năng của các vật

thuộc cơ hệ: Hình 3.20

Ttrục =

1I2 ; T

2 A

 1 P1

2 g

v 2 ; T 

1 P2 2

v

2 g B

A

B

Khi tính động năng băng tải ta chú ý rằng do tính chất không giãn của băng tải nên mọi phần tử của băng tải có vận tốc bằng nhau và bằng v: