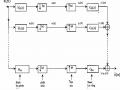
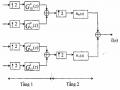
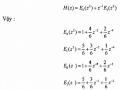Hình 3.6.1.8
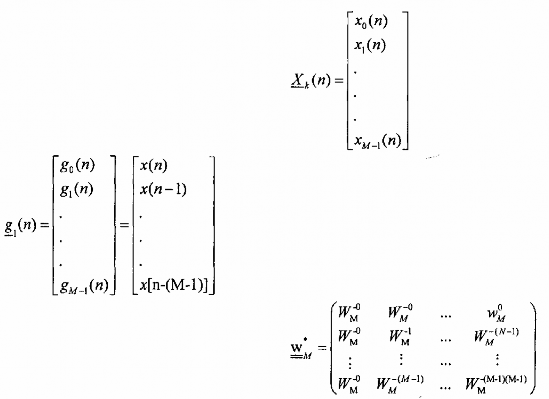
biểu diễn dưới dạng ma trận ta có:
Có thể bạn quan tâm!
-
Cấu Trúc Nhiều Pha Của Bộ Lọc Lấy Mẫu -
Cấu Trúc Nhiều Pha Của Các Bộ Lọc Biến Đổi Nhịp Hệ Số M/l Không Nguyên -
Một Vài Ứng Dụng Của Hệ Thống Lọc Số Nhiều Nhịp -
Xử lý tín hiệu số 2 Phần 2 - 12 -
Hệ Thống Khôi Phục Hoàn Hảo (Perfect Reconstruction) -
Xử lý tín hiệu số 2 Phần 2 - 14
Xem toàn bộ 140 trang tài liệu này.
từ đây hình thành bank lọc DET cho trên hình 3.6.1.9 như sau:
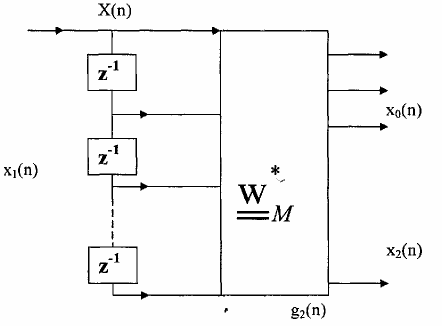
Hình 3.6.1.9
lấy biến đổi z biểu thức (3.6.1.3) ta có:
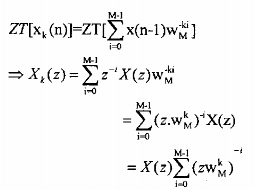
Ta gọi
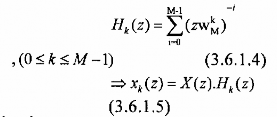
vậy ta có thể viết:
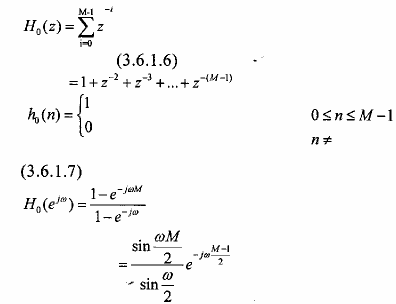
Từ đây ta có thể biết quan hệ giữa H0(z) và Hk(z) như sau:
và
(3.6.1.8)
(3.6.1.9)
vậy Hk(ej) H(e) chính là phiên bản trễ tần số đi một lượng -
2k của H0(ej)
M
(3.6.1.10)
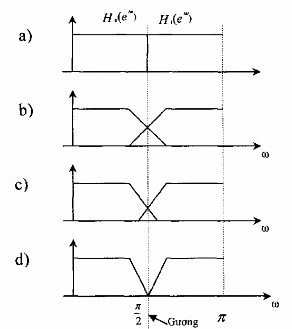
Hình (3.6.1.8) sẽ minh họa cho ta rõ quan hệ giữa H0(ej) và H1(ej) .Từ đây chúng ta có thể suy ra mối quan hệ giữa các Hk (ej) với (0 k M – 1).
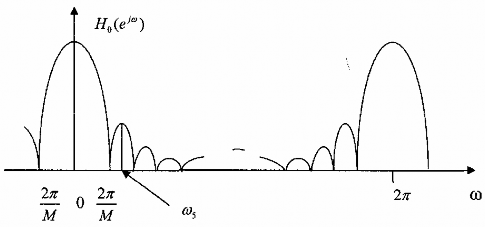
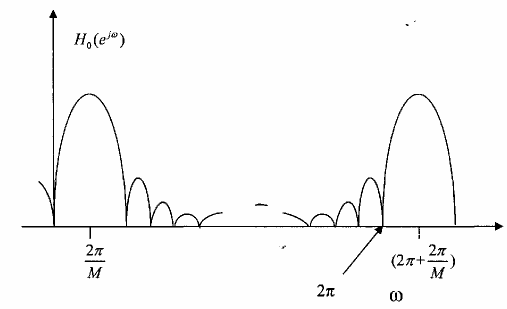
Hình 3.6.1.10
e) Biểu diễn nhiều pha bank lọc số
*Biểu diễn nhiều pha loại 1 đối với bank lọc phân tích
Trong biểu thức (3.4.2.1) chúng ta có thể biểu diễn nhiều pha loại 1 M thành phần
đối với hàm truyền đạt H(z) như sau:
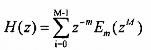
Đồi với bank lọc số phân tích gồm M bộ lọc có hàm truyền đạt là H0(z), H1(z), ..., HM-1(z) vậy với mỗi hàm truyền đạt Hk(z) chúng ta có thể biểu diễn dưới dạng phân hoạch nhiều pha như sau:
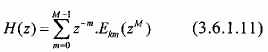
Chúng ta có thể viết biểu thức (3.6.1.11) dưới dạng sau đây đối với từng Hk(z) :
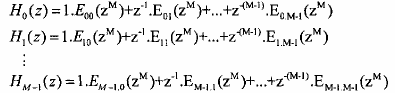
Từ đây chúng ta có thể biểu diễn biểu thức (3.6.1.13) dưới dạng ma trận sau :
(3.6.1.12)
với
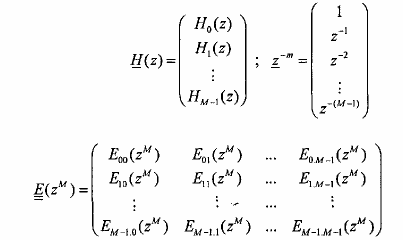
Ma trận E(zM) gọi là ma trận loại một M thành phần đối với bank lọc phân tích.
Hình 3.6.1.11 sẽ minh hoạ cấu trúc nhiều pha loại một M thành phần đối với bank lọc phân tích .
* Biểu diễn nhiều pha loại 2 đối với bank lọc tổng hợp.
Trong biểu thức (3.4.3.2) chúng ta đã có biểu diễn nhiều pha loại hai M thành phần
đối với mọt hàm truyền đạt G(z) như sau :
Đối với bank lọc số tổng hợp gồm M bộ lọc có hàm truyền đạt là G0(z), G1(z),.., GM-1(z). vậy đối với mỗi hàm truyền đạt Gk (z) chúng ta có thể biểu diễn dưới dạng phân hoạch nhiều pha loại hai M thành phần như sau:
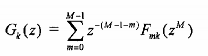
(3.6.1.13)
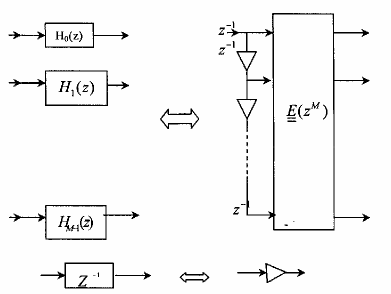
Hình 3.6.1.11
Khai triển biểu thức (3.6.1.13) đối với từng hàm truyền đạt Gk(z) chúng ta có các biểu thức sau:
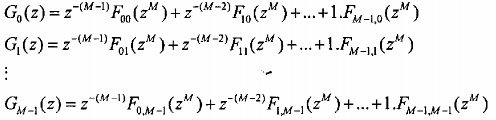
Từ đây chúng ta có thể biểu diễn biểu thức (3.6.1.13) dưới dạng ma trận sau:
(3.6.l.14)
với
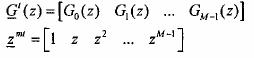
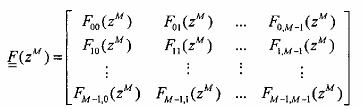
hợp.
Ma trận F(zM ) là ma trận nhiều pha loại hai M thành phần đối với bank lọc tổng
Hình 3.6.1.12 sẽ minh hoạ cấu trúc nhiều pha loại hai M thành phần đối với bank
lọc tổng hợp.
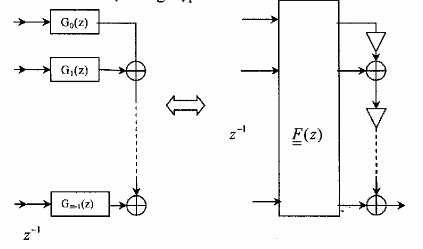
Hình 3.6.1.12
3.6.2. BANK LỌC SỐ NHIEU NHỊP HAI KÊNH
a) Bank lọc số nhiều nhịp hai kênh và bank lọc gương cầu phương QMF
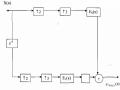
Trong phần trên, khi xét bank lọc số, sau khi bank lọc phân tích chúng ta sẽ thu được tín hiệu dải con (subband) xk (n) k M – 1). Sau đó chúng ta đã nghiên cứu bank lọc số tổng hợp. Bây giờ chúng ta sẽ kết hợp bank lọc số phân tích và bank lọc số tổng hợp với các bộ phân chia và nội suy để tạo ra bank lọc số tổng hợp nhiều nhịp. Trước hết ta nghiên cứu trường hợp M=2, ta gọi là bank lọc số nhiều nhịp hai kênh, bank lọc số nhiều nhịp này được minh hoạ trên hình 3.6.2.1.
Trong bank lọc số phân tích cho trên hình 3.6.2.1 ta thấy rằng H0(z) là bộ lọc số thông thấp, còn H1(z) là bộ lọc số thông cao. Khi thiết kế các bộ lọc số này sẽ không thể đạt được lý tưởng, tất nhiên đối với cả bộ lọc số G0(z) và G1(z) ở bank lọc tổng hợp, nên tín hiệu ra xˆ (n) của bank lọc số nhiều nhịp này sẽ khác với tín hiệu vào.
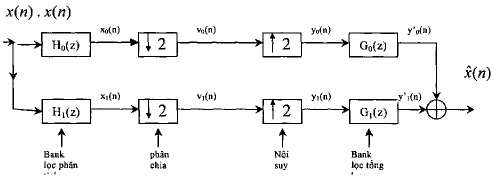
Hình 3.6.2.1
Hình 3.6.2.2 sẽ minh hoạ một vài trường hợp của đáp ứng biên độ |H0(ej)| và
|H1(ej)|.
Nhìn vào hình 3.6.2.2 ta thấy rằng |H0(ej)| và |H1(ej)| quan hệ sau đây:
Và nếu ta tưởng tượng đặt một gương phẳng vào vị trí =
2
2trên trục tần số
4
thì |H1(ej)| sẽ là ảnh gương của |H0(ej)), và theo thang tần số góc chuẩn hoá bởi tần số
lấy mẫu Fs thì
chính là một phần tư tần số lấy mẫu. Chính vì vậy băng số lọc nhiều
2
nhịp cho trên hình 3.6.2.1 được gọi là bánh lọc số gương cầu phương (Quadrature mirror filter bank: QMF), và chúng ta ký hiệu bộ lọc này bằng ba chữ đầu của tiếng anh: QM.
Trong bank lọc QMF này có ba loại sai số có thể sinh ra là: sai số do thành phần hư danh (aliasing) của |H0(ej)| và |H1(ej)| sai số do méo biên độ và sai số do méo pha.
Còn nếu dạng tín hiệu ra xâu giống hoàn toàn tín hiệu vào xˆ (u), tức là:
xˆ (n) = c.x(n - no) (3.6.2.2)
(c là hằng số )
thì bank lọc QMF này được gọi là bank lọc QMF khôi phục hoàn hảo (Perfect Reconstruction: PR) và ký hiệu là PR QMF.
Chú ý rằng thuật ngữ bank lọc số gương cầu phương (QMF) dược giải thích đối với bank lọc số hai kênh, nhưng sau này ta cũng dùng thuật ngữ này đối với bank lọc số M kênh.
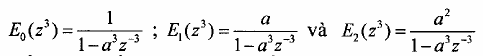
Giải
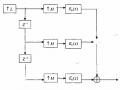
Hãy vẽ cấu trúc nhiều pha 3 thành phần của H(z).
Cấu trúc nhiều pha 3 thành phần của H(z) được cho trên hình (3.4.2.2)
