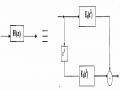
Hình 3.5.3.3
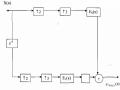
Rõ ràng cấu trúc trên hình 3.5.3.3 hơn hẳn cấu trúc trên hình 3.5.3.2 vì chúng ta tận dụng được hết khả năng ưu việt có thể khai thác được.
c) Cấu trúc nhiều pha loại 2 của bộ lúc biến đổi nhịp hệ số M/L không nguyên
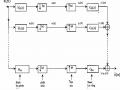
Cấu trúc nhiều pha loại 2 của bộ lọc hiến đổi nhịp hệ số M/L cho trên hình 3. 5.3.4.
Nhận xét:
- Cấu trúc trên hình 3.5.3.4 là cấu trúc nhiều pha loại 2 L thành phần của HM/L gọi tắt là HM/L nhiều pha L thành phần.
- Cấu trúc nhiều pha loại 2 này không cho ta những ưu việt câu cấu trúc nhiều pha, vì vậy chúng ta phải biến đổi sơ đồ này đi.
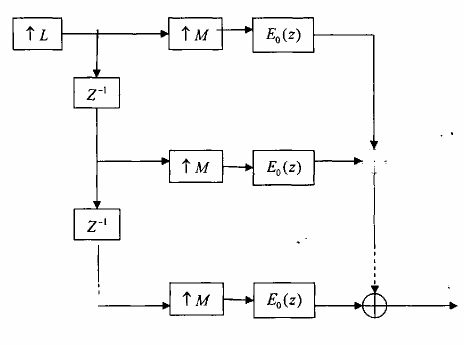
Áp dụng tính phân phối vào phép cộng của phép nội suy và sử dụng sự đồng nhất của hai sơ đồ (a) và (b) trên hình 3.3.2.2 ta có thể chuyển cấu trúc trên hình 3.5.3.4 thành cấu trúc trên hình 3.5.3.5 mà kết quả ở đầu ra cũng vẫn không có gì thay đổi.
Có thể bạn quan tâm!
-
Xử lý tín hiệu số 2 Phần 2 - 7 -
Cấu Trúc Nhiều Pha Của Bộ Lọc Lấy Mẫu -
Cấu Trúc Nhiều Pha Của Các Bộ Lọc Biến Đổi Nhịp Hệ Số M/l Không Nguyên -
Xử lý tín hiệu số 2 Phần 2 - 11 -
Xử lý tín hiệu số 2 Phần 2 - 12 -
Hệ Thống Khôi Phục Hoàn Hảo (Perfect Reconstruction)
Xem toàn bộ 140 trang tài liệu này.
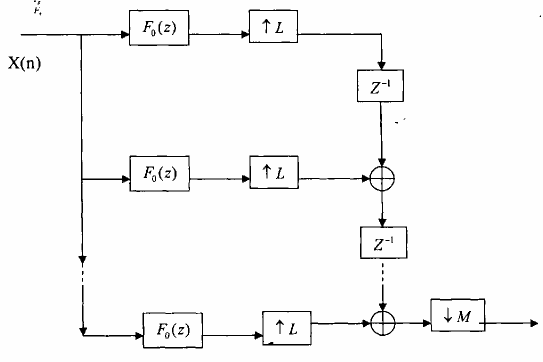
Hình 3.5.3.5
Ta thấy rằng cấu trúc trên hình 3.5.3.5 hơn hẳn cấu trúc trên hình 3.5.3.4 vì chúng ta tận dụng được hết những khả năng ưu việt có thể khai thác được.
Ví dụ 3.5.3.1
Hãy tìm cấu trúc nhiều pha loại 1 hai thành phần và loại 2 ba thành phần của bộ lọc biến đổi H213.
Giải
Dựa vào cấu trúc cho trên hình 3.5.3.3 và hình 3.5.3.5 chúng ta có kết quả cho trên hình 3.5.3.6.
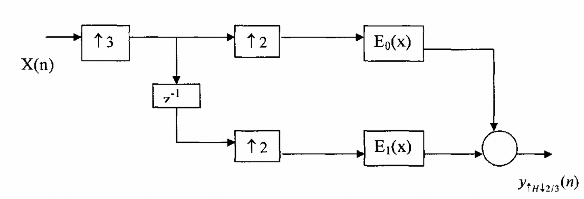
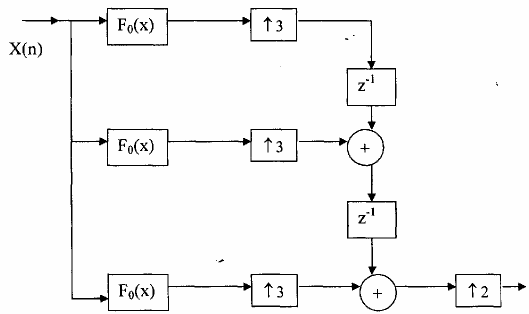
Hình 3.5.3.6
Ta thấy rằng kết quả của hai cấu trúc trên hình 3.5.3.6 (a) và (b) là như nhau, ta có thể dùng cấu trúc nào cũng được. Nhưng đối với hình 3.5.3.6 (a) nếu ta dùng thêm một thủ thuật nhỏ là z-1 = z-3z-2 thì ta sẽ có kết quả khả quan hơn. Cụ thể nếu ta dùng thủ thuật này sau đó lợi dụng sự đồng nhất (3.3.2.11) và (3.3.1.11) sau đó lợi dụng sự tương đương (3.2.4.5) tức là đổi chỗ L và M.
3.6. MỘT VÀI ỨNG DỤNG CỦA HỆ THỐNG LỌC SỐ NHIỀU NHỊP
Bây giờ chúng ta sẽ nêu một ứng dụng tiêu biểu của các hệ thống lọc số nhiều nhịp.
3.6.1. BANK LỌC SỐ
a) Định nghĩa bank lọc số.
Bank lọc số là môn tập hợp các bộ lọc số với cùng chung một đầu vào và nhiều đầu ra hoặc với nhiều đầu vào và chung một đầu ra.
Từ định nghĩa trên ta thấy rằng chó hai loại bank lọc số là bánh lọc phân tích và bank lọc tổng hợp.
b) Định nghĩa bank lọc số phân tích
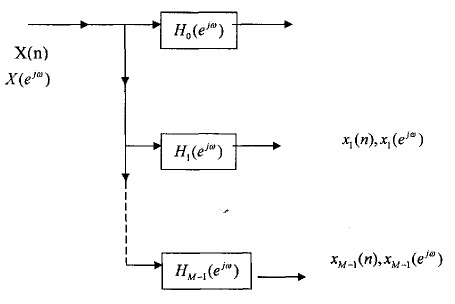
Bank lọc số phân tích là tập hợp các bộ lọc số có đáp ứng tần số là Hk(ej) được nối với nhau theo kiểu một đầu vào nhiều đầu ra, cấu trúc của bank lọc số phân tích được minh họa trên hình 3.6.1.1.
Hình 3.6.1.1
Theo hình 3.6.1.1 ta thấy rằng tín hiệu x(n) đưa vào đầu vào và được phân tích thành M tín hiệu ở đầu ra là xk(n) (0 k M - 1), như vậy trong miền tần số mỗi tín hiệu Xk(n) sẽ chiếm một dải tần số con trong dải tần của X(n) nên M tín hiệu Xk(n) được gọi là tín hiệu dải con (Subband).
Còn các bộ lọc số H0(ej) sẽ là bộ lọc thông thấp, H1(ej) đến HM-2(ej) sẽ là các bộ lọc số thông giải còn HM-1(ej) sẽ là bộ lọc thông cao, mà các tần số cắt của các bộ lọc số này sẽ kế tiếp nhau. Như vậy các bộ lọc H0(ej) , H1(ej) , ... HM-1 (ej) được gọi là các bộ lọc phân tích, còn tập hợp các bộ lọc hay {H0(ej) , H1(ej), ... HM-1(ej)} được gọi là bánh lọc phân tích .
Ví dụ 3.6.1.1
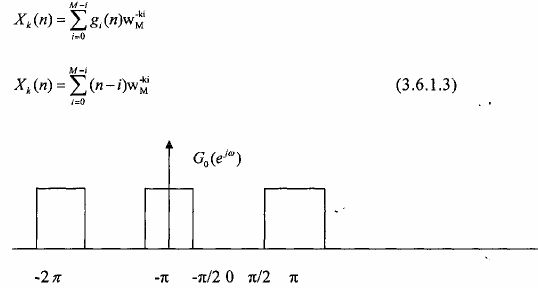
Cho bộ lọc số phân tích lý tưởng với hệ số M = 2, tín hiệu vào bank lọc là X(n) có phổ là X(ej) được cho trên hình 3.6.1.2 sau đây:
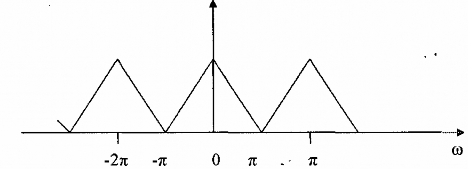
Hình 3.6.1.2.
+ Hãy vẽ sơ đồ bank lọc số phân tích này.
+ Hãy dùng đồ thị tần số đẻ giải thích dạng phổ của tín hiệu ra.
Giải
Theo sơ đồ tổng quát của bank lọc phân tích cho trên hình 3.6.1.1 thay M=2 ta sẽ có
bánh lọc phân tích 2 kênh được minh họa trên hình 3.6.1.3 trong đó có hai bộ lọc số lý
tưởng ; H0(ej) là bộ lọc thông tháp lý tưởng với tần số cắt là c =
H1(ej) là bộ lọc số
2
thông cao lý tưởng với tần số cắt là c = .
2
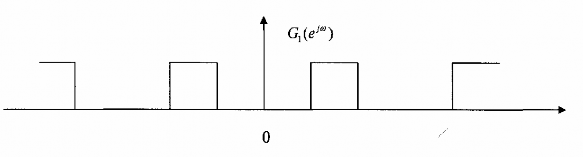
Đồ thị tần số đẻ giải thích dạng phổ của tín hiệu ra là X0(ej) và X1(ej) được cho trên hình 3.6.1.4 sau đây:
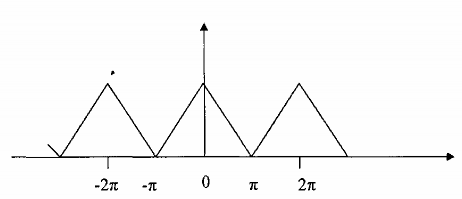
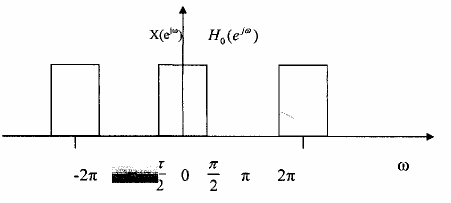
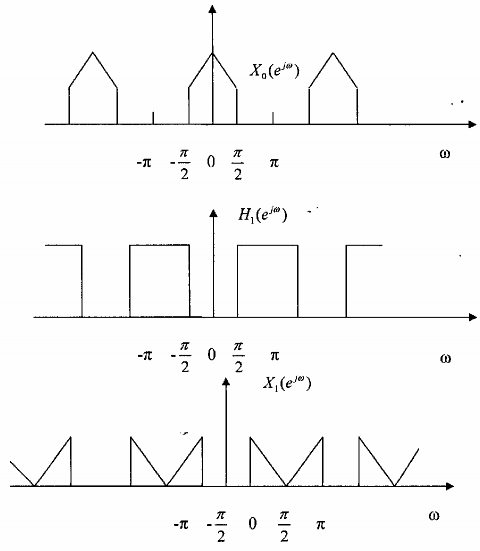
Hình 3.6.1.4
c) Định nghĩa bank lọc số tổng hợp:
Bank lọc số tổng hợp là tập hợp các bộ lọc số có đáp ứng tần số là Gk(eiw)được nối với nhau theo kiểu nhiều đầu vào và một đầu ra, cấu trúc của bank lọc số tổng hợp được minh họa trên hình 3.6.1.5:
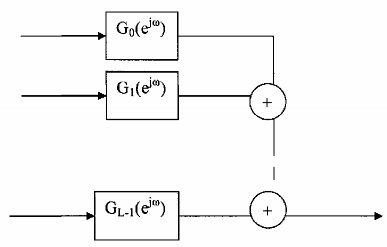
Hình 3 .6.1.5
Ví dụ:
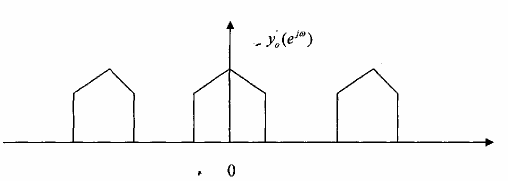
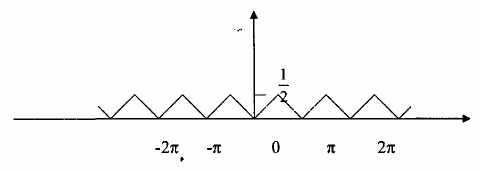
Cho bank lọc số tổng hợp !ý tưởng với hệ số M=2 có hai tín hiệu vào bank lọc số này có phổ tần là Y0(ej) và Y1(ej)có dạng cho trên hình 3.6.1.6 cần tổng hợp với nhau để được tín hiệu có phổ là Y(ej).
Giải
Hình 3.6.1.6
+ Hãy vẽ sơ đồ bank lọc số tổng hợp
+ Hãy dùng đồ thị tần số để giải thích dạng phổ của tín hiệu đầu ra
Theo sơ đồ tổng quan của bank lọc số tổng hợp cho trên 3.6.1.5 thay m=2 tạ có
bánh lọc tổng hợp hai kênh được minh họa trên hình 3.6.1.7 trong đó G0(ej)là bộ lọc số
thông thấp lý tưởng với c =
; G1(ej) là bộ lọc thông cao lý tưởng c = .
2 2
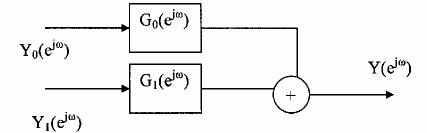
Hình 3.6.1.7
Đồ thị tần số để giải thích dạng phổ tần của tín hiệu ra được cho trên hình 3.6.1.7.
d) Bank lọc số DFT
Trong chương 4 chúng ta đã nghiên cứu biến đổi Fourier rời rạc (DFT) và chúng ta
đã biểu diễn DFT dưới dạng ma trận như sau:
wM là ma trận vuông M x M gồm các phần tử ta có biến đổi Fourier rời rạc ngược (IDFT)
M
w
M
w km . Ở đây km
j 2 km
= e M
. Tương tự
ở đây wM là liên hợp phức của ma trận wM.
Để hình thành bank lọc số DFT, giả sử ta có dãy X(n) là dãy vào, từ dãy X(n) này chúng ta tạo ra M dãy giản bằng cách cho dãy X(n) qua một đường dây trễ cụ thể ta có :
gi(n) = x(n-i)
Đầu ra của bank lọc số DFT này sẽ lả các tín hiệu Xk(n) có dạng như sau:
