Bài 3.12.
Cho một chùm tia sáng đơn sắc song song có bước sóng λ=0,7m chiếu vuông góc với m ặt của một cách tử truyền qua . Trên mặt phẳng tiêu của thấu kính hội tu ̣đặt ở sát phía sau cách tử , người ta quan sát thấy vạch quang phổ bậc ba lệch =48036′. Xác điṇ h:
1. Chu kỳ cách tử và số khe trên 1cm chiều dài của cách tử .
2. Số cưc
đaị chính nằm trong khoảng giữa hai cưc
tiểu chính b ậc nhất trong
ảnh nhiễu xạ . Cho biết mỗi khe của cách tử có đ ộ rộng b=0,7m, sin48036′=0,75.
Bài 3.13.
Một chùm ánh sáng trắng song song chiếu vuông góc vào m ặt một cách tử phẳng. Cho biết trên mỗi milimet chiều dài c ủa cách tử có n=50khe. Phía
sau cách tử đ ặt một thấu kính h ội tu.
Có thể bạn quan tâm!
-
 Tổng Hợp Dao Động Bằng Phương Pháp Giản Đồ Vectơ
Tổng Hợp Dao Động Bằng Phương Pháp Giản Đồ Vectơ -
 Vị Trí Các Cực Đại, Cực Tiểu Trong Nhiễu Xạ Qua Nhiều Khe
Vị Trí Các Cực Đại, Cực Tiểu Trong Nhiễu Xạ Qua Nhiều Khe -
 D Sin K , D Là Khoa ̉ Ng Cách Giư ̃ A Hai Nút Man
D Sin K , D Là Khoa ̉ Ng Cách Giư ̃ A Hai Nút Man -
 Vật lý đại cương 2 - 31
Vật lý đại cương 2 - 31 -
 Vật lý đại cương 2 - 32
Vật lý đại cương 2 - 32
Xem toàn bộ 258 trang tài liệu này.
Xác điṇ h hi ệu số các góc nhiêu
xa ̣ứ ng
với vac̣ h đỏ có bước sóng λ1=0,76μm nằm ở cuối quang phổ b ậc nhất và vac̣ h tím có bước sóng λ2=0,4μm nằm ở đầu quang phổ bậc hai.
Bài 3.14.
Cho một chùm tia sáng đơn sắc song song chiếu vuông góc vào m ặt của một cách tử phẳng có chu kỳ d=2μm. Xác điṇ h bậc lớn nhất của các vac̣ h cưc̣
đaị trong quang phổ nhiêu
xa ̣cho bởi cách tử đối với ánh sáng đỏ có bước
sóng λ1=0,7μm và đối với ánh sáng tím có bước sóng λ2=0,42μm.
Chương 4.QUANG HOC
LƯƠN
G TƯ
Hiện tươn
g giao thoa , nhiêu
xạ ánh sáng là những hi ện tươn
g chứ ng tỏ
bản chất sóng của ánh sáng. Nhưng vào cuối thế kỉ 19, đầu thế kỉ 20 người ta
đã phát hiện những hiện tươn
g quang hoc
mớ i như hi ện tươn
g bứ c xạ nhi ệt,
hiệu ứ ng quang đi ện, hiệu ứ ng Compton . Những hi ện tươn
g này không thể
giải thích được bằng thuyết sóng ánh sáng . Để giải quyết những bế tắc trên ,
người ta phải dựa v ào thuyết lương tử của Planck và thuyết photon của
Einstein, tứ c là phải dưa
vào bản chất hat
của ánh sáng . Phần quang hoc
nghiên cứ u ánh sáng dưa
vào hai thuyết trên goi
là quang hoc
lươn
g tử .
Trong chươ ng này chúng ta sẽ nghiên cứ u các hi ện tươn ứng quang đi ện, hiệu ứ ng Compton cùng vớ i thuyết lươṇ thuyết photon của Einstein.
4.1. BỨ C XA ̣NHIỆT
4.1.1. Bức xạ nhiệt cân bằng
g bứ c xạ nhi ệt, hiệu g tử của Planck và
Bứ c xa ̣là hiện tương các vật bi ̣kích thích phát ra sóng điện từ . Có nhiêù
dạng bức xạ khác nhau do những nguyên nhân khác nhau gây ra : ví du ̣do tác
dụng nhiệt (miếng sắt nung đỏ , dây tóc bóng đèn cháy sáng ), do tác dun
g hóa
học (phốt pho cháy sáng trong không khí), do biến đổi năng lượng trong mạch
dao động điện từ ... Tuy nhiên phát bứ c xa ̣do tác dun
g nhi ệt là phổ biến nhất
và đươc
goi
là bứ c xa ̣nhiệt.
a. Định nghĩa bức xạ nhiệt
Bứ c xạ nhi ệt là hiện tươn
g sóng đi ện từ phát ra từ những v ật bi ̣kíc h
thích bởi tác dun
g nhiệt.
b. Bức xạ nhiệt cân bằng
Khi vật phát ra bứ c xa ,
năng lượng của nó giảm và nhi ệt độ của nó cũng
giảm theo. Ngược lại nếu vật hấp thu ̣bứ c xa,
năng lượng của nó tăng và nhi ệt
độ của nó tăng . Trong trường hơp
nếu phần nă ng lươn
g của v ật bi ̣mất đi do
phát xa ̣bằng phần nă ng lươn
g v ật thu đươc
do hấp thu,
thì nhiệt độ của vật se
không đổi theo thời gian và bứ c xa ̣nhiệt của vật cũng không đổi. Bứ c xa ̣nhiệt trong trường hợp này được gọi là bứ c xạ nhi ệt cân bằng và traṇ g thái này
đươc
goi
là traṇ g thái cân bằng nhiệt động.
4.1.2. Các đai
lươn
g đặc trưng củ a bứ c xa ̣nhiệt cân bằng
a. Năng suất phát xạ toàn phần
Xét một vật đốt nón g đươc̣
giữ ở nhi ệt độ T không
đổi (Hình 4.1). Diện tích dS của vật phát xa ̣trong một đơn
vị thời gian một nă ng lương toàn phần dT . Đaị lương
R dT T dS
(4.1)
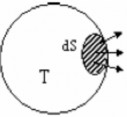
Hình 4.1
đươc̣ độ T.
goi
là năng suất phát xạ toàn phần của vật ở nhi ệt
Điṇ h nghia:
Năng suất phát xạ toàn phần của v ật ở nhi ệt độ T là một đai
lươn
g có
giá tri ̣bằng nă ng lương bứ c xạ toàn phần do m ột đơ n vi ̣di ện tích của v ật đó
phát ra trong một đơ n vi ̣thờ i gian ở nhiệt độ T.
Đơn vi ̣của nă ng suất phát xa ̣toàn phần RT trong hệ đơn vi SI là W/m2.
b. Hệ số phát xa ̣ đơn sắc
Bứ c xa ̣toàn phần do v ật phát ra ở nhi ệt độ T nói chung bao gồm nhiều bứ c xa ̣đơn sắc . Năng lượng bức xạ phân bố khô ng đồng đều cho tất cả moị
bứ c xa ̣có bước sóng khác nhau. Vì thế nă ng lương phát xa ̣ứ ng với bước sóng
thay đổi trong khoảng λ đến λ+dλ chỉ là m ột vi phân của năng suất phát xạ
toàn phần. Đaị lươn
g
r,T
dRT
d
(4.2)
đươc
goi
là hệ số phát xạ đơ n sắc của vật ở nhiệt độ T ứng với bước sóng λ.
Nó phu ̣thuộc vào bản chất và nhiệt độ của vật và phu ̣thuộc bước sóng λ
của bức xạ đơn sắc do vật phát ra.
Đơn vi ̣của hệ số phát xa ̣đơn sắc: W/m3. Bằng thưc
nghiệm ta có thể xác
điṇ h đươc rλ,T ứng với bức xạ đơn sắc bước sóng λ của vật phát ra ở nhi ệt độ
T, từ đó ta sẽ xác điṇ h đươc nă ng suất phát xa ̣toàn phần:
RT dRT r,T d(4.3)
0
c. Hệ số hấp thụ đơn sắc
Giả sử trong m ột đơn vi ̣thời gian , chùm bứ c xa ̣đơn sắc có bước sóng nằm trong khoảng từ λ đến λ+dλ gử i tới m ột đơn vi ̣di ện tích của v ật một
năng lượng dλ,T nhưng vật đó chỉ hấp thu ̣một phần nă ng lương d'λ,T. Tỉ số:
a,T
d',T
d
(4.4)
đươc
goi
,T
là hệ số hấp thu ̣ đơ n sắc của vật ở nhi ệt độ T ứng với bước sóng λ.
Nó phu ̣thu ộc vào bản chất và nhi ệt độ của v ật, phụ thuộc vào bước sóng λ
của chùm bức xạ đơn sắc gửi tới.
Thông thường vật không hấp thu ̣hoàn toàn nă ng lương của chùm bứ c xa
gử i tới, do đó aλ,T <1. Những vật mà aλ,T=1 với moi
nhi ệt độ T và moi
bước
sóng λ đươc
goi
là vật đen tuyệt đối. Trong thưc
tế không có vật đen tuyệt đối
mà chỉ có những vật có tính chất gần với tính chất của vật đen tuyệt đối, ví du
bồ hóng, than bac̣ h kim ... Để tao
ra v ật đen tuyệt đối người ta dùng m ột cái
bình rỗng cách nhi ệt, có khoét một lỗ nhỏ , mặt trong phủ m ột lớp bồ hóng .
Khi tia bứ c xa ̣lot qua lỗ vào bình , nó sẽ bi ̣phản xa ̣nhiêù lần trên thành bình ,
mỗi lần phản xa ̣nă ng lương của nó laị bi ̣bình hấp thu ̣m ột phần. Kêt́ quả có
thể coi là tia bứ c xa ̣đã bị hấp thụ hoàn toàn.
4.1.3. Điṇ h luật Kirchhoff
Giả sử đ ặt hai vật có bản chất khác nhau trong m ột bình cách nhiệt. Các vật này sẽ phát xa ̣và hấp thu ̣nhi ệt. Sau một thời gian traṇ g thái cân bằng
nhiệt động sẽ đươc thiêt́ l ập, hai vật sẽ cùng ở m ột nhiệt độ T như trong bình.
Ở trạng thái cân bằng thì hiển nhiên v ật nào phát xa ̣maṇ h thì cũng phải hấp thụ bức xạ mạnh. Từ nhận xét đó Kirchhoff đã đưa ra điṇ h luật như sau:
Tỉ số giữa h ệ số phát xạ đơ n sắc rλ,T và hệ số hấp thu ̣ đơ n sắc aλ,T của
một vật bất kì ở trang thái bứ c xạ nhi ệt cân bằng không phu ̣ thu ộc vào bản
chất của vật đó, mà chỉ phu ̣ thu ộc vào nhiệt độ T của nó và bướ c sóng λ của chùm bứ c xạ đơ n sắc.
Nghĩa là
r,T a,T
f,T
(4.5)
trong đó fλ,T là hàm số chung cho moi v ật nên
đươc
goi
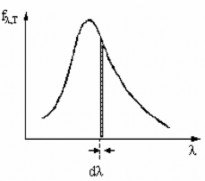
là hàm phổ biến . Vì vật đen tuyệt
đối có h ệ số hấp thu ̣đơn sắc bằng 1 nên hàm phổ biến chính là h ệ số phát xa ̣đơn sắc của vật đen tuyệt đối . Làm thí nghiệm với mô
Hình 4.2. Đườ ng đ ặc trưng phổ phát xạ của vật đen tuyệt đối
hình của vật đen tuyệt đối người ta xác điṇ h đươc
fλ,T bằng thưc
nghiệm. Hình
4.2 là đồ thi ̣của hàm phổ biến fλ,T theo bước sóng λ ở nhiệt độ T. Đường cong
này đươc
goi
là đường đ ặc trưng phổ phát xa ̣của vật đen tuyệt đối. Năng suất
phát xa ̣toàn phần của vật đen tuyệt đối đươc xác điṇ h theo công thứ c (4.3) sẽ
có tri ̣số bằng toàn b ộ diện tích giới han trục hoành λ trên Hình 4.2.
bởi đường đ ặc trưng phổ phát x ạ và
4.2. CÁC ĐIN
H LUẬT PHÁT XA ̣CỦ A VẬT ĐEN TUYỆT ĐỐ I
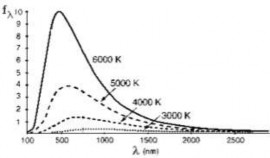
4.2.1. Điṇ h luật Stephan-Boltzmann
Hình 4.3 biểu diên
đường đ ặc trưng
phổ phát xa ̣của v ật đen tuyệt đối ở các nhiệt độ khác nhau. Ta nhận thấy khi nhiệt độ tăng, diện tích giữa đường đ ặc trưng phổ phát xạ và trục hoành λ cũng tăng theo. Như vậy nă ng suất phát xa ̣toàn
phần của v ật đen tuyệt đối phu ̣thu ộc vào
Hình 4.3
nhiệt độ của vật. Stephan (bằng thưc nghi ệm) và Boltzmann (bằng lý thuyêt́ )
đã tìm ra sự phu ̣thuộc này và đã thiết lập đươc
điṇ h luật Stephan-Boltzmann.
Nội dung định luật:
Năng suất phát xạ toàn phần của v ật đen tuyệt đối tỉ l ệ thuận vớ i lũy thừ a bậc bốn của nhiệt độ tuyệt đối của vật đó:
T
R T 4 (4.6)
trong đó σ đươc
goi
là hằng số Stephan-Boltzmann, σ =5,6703.10-8 W/m2K4.
4.2.2. Điṇ h luật Wien
Nhìn trên hình 4.3 ta thấy rằng mỗi đường đ ặc trưng phổ phát xa ̣của v ật
đen tuyệt đối ở m ột nhiệt độ T nhất điṇ h đều có m ột cưc đaị ứ ng với m ột giá
trị xác định của bước sóng được ký hi ệu là λmax và khi nhiệt độ tăng thì bước sóng λmax giảm. Đối với v ật đen tuyệt đối thì những bứ c xa ̣có bước sóng lân
cận giá tri ̣của λmax là bứ c xa ̣mang nhiều nă ng lương nhất . Nghiên cứ u mối
quan hệ điṇ h lương giữa bước sóng λmax và nhiệt độ T của vật đen tuyệt đối,
năm 1817 Wien đã tìm ra điṇ h luật mang tên ông.
Nội dung điṇ h luật:
Đối với vật đen tuyệt đối, bước sóng λmax của chùm bức xạ đơn sắc mang
nhiều nă ng lương nhất tỷ lệ nghịch với nhiệt độ tuyệt đối của vật đó.
b
max
T
(4.7)
với b =2,898.10-3m.K đươc
goi
là hằng số Wien.
4.2.3. Sư ̣ khủ ng hoảng ở vùng tử ngoaị
Xuất phát từ quan ni ệm của v ật lí cổ điển coi các nguyên tử và phân tư
phát xạ ho ặc hấp thu ̣ nă ng lươn
g m ột cách liên tuc
, Rayleigh-Jeans đã tìm
đươc công thứ c xác điṇ h hệ số phát xa ̣đơn sắc của vật đen tuyệt đối như sau:
f,T
22
kBT
c2
(4.8)
trong đó kB là hằng số Boltzmann , T là nhiệt độ tuyệt đối, ν là tần số của bứ c xạ đơn sắc (tần số và bước sóng liên hệ với nhau qua công thứ c ν=c/λ).
Theo công thứ c (4.8), fν,T tỉ lệ với lũy thừ a b ậc 2 của ν, nên fν,T sẽ tăng
rất nhanh khi ν tăng (tứ c λ giảm). Công thứ c này chỉ phù hơp
với thưc
nghiệm
ở vùng tần số nhỏ (bước sóng lớn ), còn ở vùng tần số lớn (bước sóng nhỏ ), tứ c là vùng sóng tử ngoại, nó sai lệch rất nhiều . Bế tắc này tồn taị suốt trong
khoảng thời gian dài cuối thế kỷ 19 và đươc ngoại.
goi
là sự khủng hoảng ở vùng tư
Mặt khác, từ công thứ c (4.8) ta có thể tính đươc phần của một vật đen tuyệt đối ở nhiệt độ T:
nă ng suất phát xa ̣toàn
R f
d2kBT 2 d(4.9)
T ,T 0
c2 0
Năng lượng phát xạ toàn phần của v ật ở m ột nhiệt độ T nhất điṇ h laị bằng vô cùng. Điều này là sai. Sở di ̃ có kết quả vô lí đó là do quan ni ệm vật lí
cổ điển về sự phát xa ̣và hấp thu ̣nă ng lương bứ c xa ̣m ột cách liên tuc̣ . Để giải
quyết những bế tắc trên , Planck đã phủ điṇ h lí thuyết cổ điển về bứ c xa ̣và đề
ra một lí thuyết mới goi
là thuyết lươn
g tử nă ng lương.
4.3. THUYẾ T LƯƠN
G TỬ PLANCK
4.3.1. Thuyết lươn
g tử nă ng lươn
g củ a Planck
Các nguyên tử và phân tử phát xạ hay hấp thu ̣ nă ng lươn
g của bứ c xa
điện từ m ột cách gián đoan
, nghĩa là phần năng lượng phát xạ hay hấp
thụ luôn là bội số nguyên của một lươn
g nă ng lươn
g nhỏ xác điṇ h goi là
lượng tử năng lượng hay quantum năng lượng.
Một lươn λ là:
g tử nă ng lươn
g của bứ c xạ điện từ đơ n sắc tần số ν, bước sóng
trong đó:
hh c
(4.10)
h là hằng số Planck, h = 6,625.10-34Js,
c là vận tốc ánh sáng trong chân không.
Công thức Planck
Xuất phát từ thuyết lươn
g tử , Planck đã tìm ra công thứ c của hàm phô
biến, tứ c là hệ số phát xa ̣đơn sắc của vật đen tuyệt đối như sau:
f,T
22
c2
h
h
ekBT1
(4.11)
trong đó kB là hằng số Boltzmann, T là nhiệt độ tuyệt đối.
4.3.2. Thành công củ a thuyết lương tử nă ng lương
Công thứ c Planck cho phép ta vẽ đươc đường đ ặc trưng phổ phát xa ̣ của
vật đen tuyệt đối phù hơp
với kết quả thưc
nghi ệm ở moi
vùng nhi ệt độ
và moi vùng tần số khác nhau.
Từ công thứ c Planck ta có thể suy đươc
công thứ c của Rayleigh và Jeans
và các công thứ c thể hiện các điṇ h luật của vật đen tuyệt đối. Trong miền
h
tần số nhỏ sao cho hν << kT thì ekBT1 h. Do đó công thứ c Planck
kBT
sẽ thành : f
22
, ta laị thu đuơc
công thưc cua Rayleigh và
Jeans.
,T
kBT
c2
Từ công thứ c Planck ta tìm đươc
điṇ h lu ật Stephan-Boltzmann: Năng
suất phát xa ̣toàn phần của v ật đen tuyệt đối taị m ột nhiệt độ T nào đó bằng:
22 h4 2k2 4
RT
0
f,T d
0 c2
h
ekBT1
d
15
T
c2h3
T
Cuối cùng ta đươc R T 4 trong đó σ=5,6703.10-8W/m2.K4. Đây chính
là điṇ h luật Stephan-Boltzmann.
Từ công thứ c Planck ta tìm đươc̣
điṇ h luật Wien. Nếu ta lấy đao
hàm của
fν,T theo ν và cho nó triệt tiêu rồi tìm νmax (hay λmax) tại các nhiệt độ khác
nhau, kết quả thu đươc Wien.
là λmaxT=2,8978.10-3mK. Đây chính là điṇ h lu ật