4.4. THUYẾT PHOTON CỦA EINSTEIN
4.4.1. Thuyết photon củ a Einstein
Thuyết lương tử của Planck đã nêu lên quan điêm̉ hi ện đaị về nă ng
lượng: năng lượng đi ện từ phát xa ̣hay hấp thu ̣có những giá tri ̣gián đoan ,
chúng luôn là bội nguyên của lượng tử năng lượng ε. Ta nói rằng năng lượng
điện từ phát xạ hay hấp thu ̣ bi ̣lương tử hoá . Nhưng thuyết lượng tử của
Planck chưa nêu đươc
bản chất gián đoan
của bứ c xa ̣đi ện từ . Năm 1905,
Einstein dưa
trên thuyết lươ ̣ ng tử về nă ng lươn
g của Planck đã đưa ra thuyết
lượng tử ánh sáng (hay thuyết photon).
Nội dung thuyết photon của Einstein:
a. Bứ c xạ điện từ gồm vô số những hat hay photon.
rất nhỏ goi
là lươn
g tử ánh sáng
b. Vớ i môi
bứ c xạ điện từ đơ n sắc nhất điṇ h, các photon đều giống nhau
và mang một nă ng lươn
g xác điṇ h bằng nhau.
c. Trong chân không các photon đươc c = 3.108 m/s.
truyền đi vớ i cùng v ận tốc
d. Khi một vật phát xạ hay hấp thu ̣ bứ c xạ đi ện từ c ó nghia phát xạ hay hấp thu ̣ các photon.
là v ật đó
e. Cường độ của chùm bức xạ tỉ lệ vớ i số photon phát ra từ nguồn trong một đơ n vi ̣thờ i gian.
4.4.2. Động lưc
hoc
photon
Năng lượng của photon ứ ng với một bứ c xa ̣điện từ đơn sắc tần số ν là:
h(4.12)
Khối lương của photon:
m hh
(4.13)
c2 c2 c
Theo thuyết tương đối
1
v2
c2
m m0
m0 m
1
v2
c2
Vận tốc của photon bằng c, do đó m0=0.
Vậy photon có khối lương nghỉ bằng 0.
Động lươn
g của photon
p mc hh
(4.14)
c
Như vậy động lương của photon tỉ lệ thuận với tần số và tỉ l ệ nghịch với
bước sóng của bức xạ điện từ .
4.5. HIỆN TƯƠṆ
4.5.1. Điṇ h nghia
G QUANG ĐIỆN
Hiệu ứ ng bắn ra các electro n từ m ột tấm
kim loai
khi roi
vào tấm kim loai
đó m ột bứ c xa
điện từ thích hơp
đươc
goi
là hi ện tươn
g quang
điện. Các electron bắn ra đươc electron.
goi
là các quang
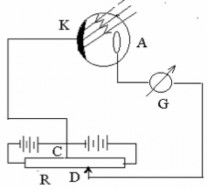
Hình 4.4. Thí nghiệm quang điện
Để nghiên cứ u hi ện tượng quang đi ện
người ta đã làm thí nghiệm vớ i tế bào quang điện như sau:
Tế bào quang đi ện gồm m ột bình chân không có hai bản cưc
làm bằng
kim loaị : bản cực dương anốt A và bản cưc
âm catốt K. Catốt làm bằng kim
loại ta cầ n nghiên cứ u . Tế bào quang đi ện đươc mắc như hình vẽ . Nhờ biêń
trở ta có thể thay đổi hiệu điện thế U giữa A và K về độ lớn và chiều.
Khi roi
chùm bứ c xa ̣đi ện từ đơn sắc bước sóng λ thích hơp
vào catốt K,
chùm ánh sáng này sẽ giải phóng các electron khỏi mặt bản cưc
âm K. Dưới
tác dun
g của đi ện trường giữa A và K, các quang electron sẽ chuyển động về
cưc
dương anốt, tạo ra trong mạch dòng quang đi ện. Thay đổi hiệu điện thế U
giữa A và K ta đươc đồ thị dòng quang điện như Hình 4.5.
Nhận xét
UAK>0: Khi UAK tăng thì I tăng theo, khi UAK đaṭ đến m ột giá tri ̣nào đó
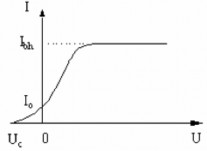
cường độ dòng quang điện sẽ không tă ng nữa và đaṭ giá tri ̣ Ibh, đươc là cường độ dòng quang điện bão hòa.
Khi UAK=0 cường độ dòng quang điện vâñ có giá tri ̣ I0. Điều đó chứ ng tỏ quang electron bắn ra đã có sẵn m ột động nă ng ban đầu.
goi
Để tri ệt tiêu dòng quang điện ta phải đ ặt
Hình 4.5. Đồ thị I-V
lên A-K một hiệu điện thế ngươc Uc sao
cho công cản của đi ện trường ít nhất phải bằng đ ộng nă ng ban đầu cưc đaị của các electron bị bứt khỏi bản K, nghĩa là:
eU 1 mv2 (4.15)
c 2 o max
Uc đươc
goi
là hiệu điện thế cản.
4.5.2. Các điṇ h luật quang điện và giải thích
Từ các kế t quả thí nghi ệm người ta đã tìm ra ba điṇ h lu ật sau đây goi là
ba điṇ h luật quang điện. Các điṇ h luật này chỉ có thể giải thích đươc thuyết photon của Einstein.
a. Phương trình Einstein
dưa
vào
Khi có một chùm ánh sáng thích hơ ̣ p rọi đến catốt , các electron tự do trong kim loaị hấp thu ̣photo n. Mỗi electron hấp thu ̣m ột photon và sẽ nh ận
đươc
một nă ng lươn
g bằng hν . Năng lượng này m ột phần chuyển thành công
thoát Ath electron ra khỏi kim loaị , phần còn lại chuyển thành đ ộng nă ng ban đầu của quang electron. Động nă ng ban đầu càng lớn khi electron càng ở gần
mặt ngoài kim loại, vì đối với các electro n ở sâu trong kim loai
, một phần
năng lượng m à nó hấp thu ̣đươc của photo n sẽ bi ̣ tiêu hao trong quá trình
chuyển động từ trong ra m ặt ngoài kim loaị . Như vậy động nă ng ban đầu se
cưc
đaị đối với các electron ở sát mặt ngoài kim loaị.
Theo điṇ h luật bảo toàn nă ng lươn hiệu ứ ng quang điện:
g, Einstein đã đưa ra phương trình cho
h c A 1 mv2 (4.16)
th 2 o max
b. Điṇ h luật về giớ i han
Phát biểu:
quang điện
Đối với mỗi kim loại xác định , hiện tương quang đi ện chỉ xảy ra khi
bước sóng λ của chùm bức xạ đi ện từ roị
λo gọi là giới hạn quang điện của kim loai
tớ i nhỏ hơn một giá tri ̣xác điṇ h λo, đó.
Giới han quang đi ện λo phụ thuộc vào bản chất của kim loaị làm catốt .
Điṇ h luật này nói lên điều kiện cần để có thể xảy ra hi ện tươn
g quang điện. Ở
đây cần nhấn maṇ h rằng , nếu chùm sáng tới có bước sóng λ>λo thì dù cường
độ sáng rất maṇ h, nó cũng không thể gây ra hiện tươn
Giải thích:
Trong phương trình Einstein:
g quang điện.
h c A 1 mv2
th 2 o max
Vì v2 0 và đặt A
h c
nên
o max
th
0
0
h c h c
0
Nghĩa là chùm ánh sáng gây ra hi ệu ứ ng quang điện phải có bước sóng λ
nhỏ hơn m ột giá tri ̣xác điṇ h 0
hc Ath
(λ<λo ). λo chính là giới han
quang đi ện
và rò ràng nó chỉ phu ̣ thuộc vào công thoát Ath, tứ c là phu ̣thu ộc vào bản chất kim loaị làm catốt.
c. Điṇ h luật về dòng quang điện bão hoà
Phát biểu:
Cường độ dòng quang điện bão hoà tỉ lệ vớ i cườ ng độ của chùm bức xạ
rọi tới.
Giải thích:
Cường độ dòng quang điện tỉ lệ với số quang electron thoát ra khỏi catốt đến anốt trong m ột đơn vi ̣thời gian . Dòng quang điện trở nên bão hoà khi số quang electron thoát khỏi catốt đến anốt trong đơn vi ̣thời gian là không đổi. Số quang electron thoát ra khỏi catốt tỉ lệ với số photon bị hấp thụ. Số photon bị hấp thụ lại tỉ l ệ với cường đ ộ của chùm bức xạ . Do đó cường đ ộ dòng quang điện bão hoà tỉ lệ thuận với cường độ chùm bứ c xa ̣rọi tới:
Ibh ~ Ne; Ne ~ Np; Ne ~ It Ibh ~ It
d. Điṇ h luật về động nă ng ban đầu cực đại của quang electron
Phát biểu:
Động nă ng ban đầu cưc
đai
của quang electron không phu ̣ thu ộc vào
cường độ chùm bứ c xạ roi đó.
tớ i mà chỉ phu ̣ thu ộc vào tần số của chùm bứ c xa
Giải thích:
h c A
1 mv2 h c
1 mv2
th 2
o max
0 2
o max
1 mv2 hc( 1 1 ) (4.17)
2 o max
0
Ta thấy rò đ ộng nă ng ban đ ầu cực đại của quang electro n chỉ phu ̣thu ộc vào tần số của chùm bức xạ đi ện từ , mà không phu ̣thu ộc vào cường đ ộ của bứ c xa ̣đó.
Thuyết photon đã giải thích đươc tất cả các điṇ h lu ật quang điện, nó đã
đưa ra m ột quan niệm mới về bản chất ánh sáng . Theo Einstein, mỗi photon
có một nă ng lương ε=hν. Tính chất haṭ thể hi ện ở năng lượng ε gián đoan .
Tính chất sóng thể hiện ở tần số ν (và λ) của ánh sáng.
Như v ậy ánh sáng vừ a có tính sóng , vừ a có tính hat sáng có lưỡng tính sóng-hạt.
. Ta nói rằng ánh
4.6. HIỆU Ứ NG COMPTON
Hiệu ứ ng Compton là m ột trong những hi ệu ứ ng thể hi ện bản chất haṭ của các bức xạ đi ện từ , đồng thờ i nó
chứ ng minh sự tồn tai
đ ộng lươn
g của
các hat photon.
4.6.1. Hiệu ứ ng Compton
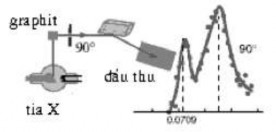
Thí nghiệm Compton
Hình 4.6. Thí nghiệm Compton
Cho một chùm tia X bước sóng λ chiếu vào graphit hay paraphin... Khi đi
qua các chất này tia X bị tán xạ theo nhiều phương . Trong phổ tán xa ̣, ngoài vạch có bước sóng λ bằng bước sóng của chùm tia X chiếu tới, còn có những
vạch ứng với bước sóng λ′>λ (Hình 4.6). Thưc
nghi ệm chứ ng tỏ rằng bước
sóng λ′ không phụ thuộc cấu tao
thuộc vào góc tán xạ θ.
của các chất đươc
tia X rọi đến mà chỉ phụ
Độ tăng của bước sóng Δλ=λ'-λ đươc xác điṇ h bởi biêủ thứ c:
2c
sin2
2
trong đó λc=2,426.10-12m là một hằng số chung cho moi bước sóng Compton.
chất , đươc
goi là
Theo lí thuyết sóng thì khi tia X truyền đến thanh graphít nó làm cho các hạt mang đi ện trong thanh (ở đây là electro n) dao động cưỡng bứ c với cùng
tần số của tia X, do đó các bứ c xa ̣tán xa ̣về moi phương phải có cùng tần sô
với bứ c xa ̣tới . Như vậy lí thuyết sóng đi ện từ cổ điển không giải thích đươc
hiện tươn
g Compton.
4.6.2. Giải thích hiệu ứ ng Compton bằng thuyết lương tử ánh sáng
Chúng ta có thể coi hi ện tươn
g tán xa ̣tia X như một va cham
hoàn toàn
đàn hồi giữa m ột photon và một electron trong chất mà tia X chiếu tới (Hình 4.7). Trong phổ tán xa,̣ những vac̣ h có bước sóng bằng bước sóng của tia X
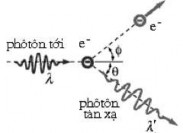
chiếu tới tương ứ ng với sự tán xa ̣của tia X lên các electron ở sâu trong nguyên tử , các electron này liên kết maṇ h với haṭ nhân, còn vac̣ h có bước sóng λ′>λ tương ứng với sự tán xạ tia X lên các
electron liên kết yếu với haṭ nhân . Năng lương
liên kết của các electron này rất nhỏ so với nă ng
Hình 4.7. Va cham
đàn hồi
lượng của chùm tia X chiếu tới , do đó các electron đó có thể coi như tự do.
giữa photon và electron
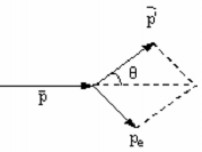
Giả thiết trước va cham electro n (e-) đứ ng
yên. Tia X có nă ng lương lớn , khi tán xa ̣trên
electron tự do tia X sẽ truyền năng lượng cho
electron nên sau va chaṃ lớn, do đó ta phải áp dun
v ận tốc của electron rất
g hi ệu ứ ng tươ ng đối
tính trong trường hơp
này.
Hình 4.8
Chúng ta xét động lươn
g, năng lượng của
hạt photon và electron trước và sau va cham:
Photon | Eletron | Hệ photon + electron | ||
Động lượng | Trước va chạm | p hh c | 0 | p |
Sau va chạm | p' h'h c ' | p' mev e v2 1 c2 | p'p'e | |
Năng lượng | Trước va chạm | hhc | m c2 e e | hm c2 e e |
Sau va chạm | ' h' hc ' | m c2 e 'e v2 1 c2 | m c2 ' 'e h ' e v2 1 c2 |
Có thể bạn quan tâm!
-
 Vị Trí Các Cực Đại, Cực Tiểu Trong Nhiễu Xạ Qua Nhiều Khe
Vị Trí Các Cực Đại, Cực Tiểu Trong Nhiễu Xạ Qua Nhiều Khe -
 D Sin K , D Là Khoa ̉ Ng Cách Giư ̃ A Hai Nút Man
D Sin K , D Là Khoa ̉ Ng Cách Giư ̃ A Hai Nút Man -
 Đu ̛ Ơ ̀ Ng Đ Ặc Tru ̛ Ng Phổ Phát Xạ Cu ̉ A Vật Đen Tuyệt Đối
Đu ̛ Ơ ̀ Ng Đ Ặc Tru ̛ Ng Phổ Phát Xạ Cu ̉ A Vật Đen Tuyệt Đối -
 Vật lý đại cương 2 - 32
Vật lý đại cương 2 - 32
Xem toàn bộ 258 trang tài liệu này.
Do hệ là hệ kín, va chạm là đàn hồi nên áp dụng điṇ h luật bảo toàn năng
lượng và động lươn
g ta có:
e''e(6.18)
p p'p'e(6.19)
trong đó me là khối lượng nghỉ của eletron.
Gọi góc ( p, p') . Từ (4.19) p'e p p' . Bình phương hai vế ta được:
e
p'2 p2 p'2 2 pp'cos(4.20)
Áp dụng công thức liên h ệ giữa nă ng lươn tương đối tính:
g và đ ộng lươn
g trong cơ hoc
0
E2 m2c4 p2c2
chú ý rằng, photon có khối lượng nghỉ bằng 0 nên với photon: E2 p2c2.
Thay biểu diễn động lượng theo năng lượng vào (4.20), ta được:
e e
'2 m2c4 2
c2 c2
'2
c2
2'cos
c2
'2 m2c4 2 '2 2'cos(4.21)
e e
Từ (4.18), ta có: 'e e '. Bình phương hai vế ta được:
'2 2 2' 2 '2 2' (4.22)
e e e e
Trừ (4.21) cho (4.22) rút ra:
2' 2m2c4 2'(1 cos)
e e e e
Mặt khác: 'e
e
', e
m c2
e
2(e
')e
22 2'(1 cos)
e
(')e '(1 cos)
m c2 (') h'(1 cos) 2h'sin2
e2